Параллельность прямой и плоскости

Прямая параллельна плоскости, если она параллельна какой-либо прямой, принадлежащей этой плоскости.

Прямая параллельна плоскости, если через эту прямую можно провести плоскость параллельную данной.

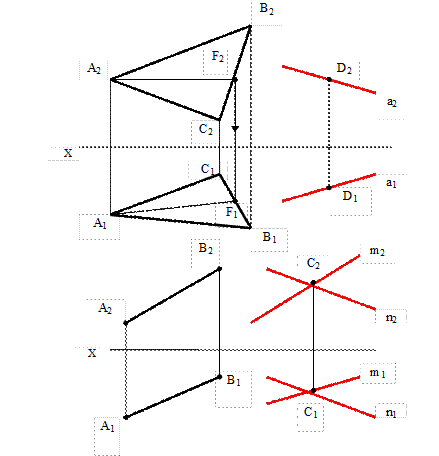
Дано: Σ(∆ ABC), D

Найти: a II Σ

Решение:

1. AF є Σ → A₂F₂, A₁F₁

2. a₂ II A₂F₂, a₁ II A₁F₁

Через точку D можно провести множество прямых II Σ, т.к. AF выбрано произвольно.

Можно вспомогательную прямую AF заменить любой стороной треугольника.

__________________________

Дано: AB, C

Найти:∆ II AB; ∆С

Решение:

Задача имеет множество решений

1. m II AB → m₂ II A₂B₂, m₁ II A₁B₁

2. Произвольно проводим прямую

n → n₁, n₂

3. ∆(m ∩ n) будет II AB, т.к. m є ∆, m II AB.

Можно было задать плоскость треугольником.

Пересечение плоскостей

Две плоскости пересекаются по прямой линии, положение которой определяется двумя точками, одновременно принадлежащими этим плоскостям. Способ, с помощью которого определяются эти точки, называется способом вспомогательных сечений. Суть способа: 1. Заданные плоскости пересекаются двумя плоскостями -,,посредниками”, чаще всего плоскостями уровня. 2. Определяются линии пересечения плоскостей -,,посредников” с каждой из заданных плоскостей. 3. Находится точка пересечения каждой пары полученных линий. 4. Через две точки проводится прямая, являющаяся линией пересечения двух плоскостей. 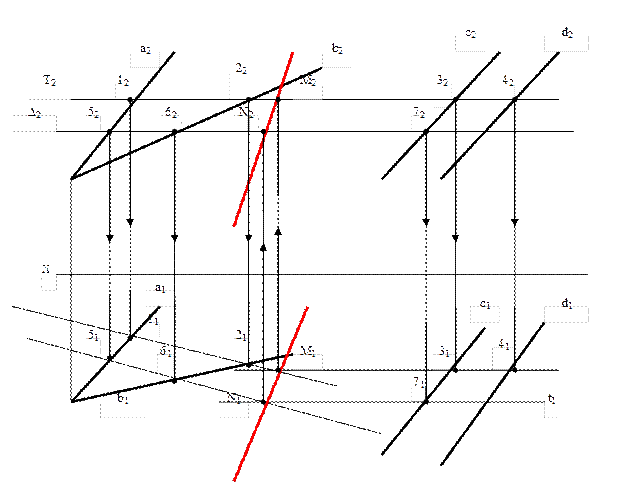Дано: Q(a ∩ b) Σ(c II d) Найти: MN=Q ∩ Σ Решение: 1. Q II П₁ → Q₂ II OX a ∩ Q=12 → 1₂2₂ ↓ 1₁2₁ T ∩ Σ=34 → 3₂4₂ ↓ 3₁4₁ 2. ∆ II П1 → ∆₂ II OX ∆ ∩ Q=56 → 5₂6₂ ↓ 5₁6₁ ∆ ∩ Σ=t7 II 34 → 7₂ → 7₁ → t₁II 3₁4₁ 3. 12 ∩ 34=M → 1₁2₁∩3₁4₁=M₁ ↑ M₂ є T₂ (след-проекция, собир. св-во). 4. 56 ∩ t=N → 5₁6₁ ∩ t₁=N₁ ↑ N₂ є ∆₂ (-..-..-..) 5. M U N=MN → M₁U N₁=M₁N₁, M₂ U M₂=M₂N₂. Частный случай пересечения плоскостей, когда одна из них плоскость уровня. Плоскость уровня пересекает другую плоскость по линии уровня. 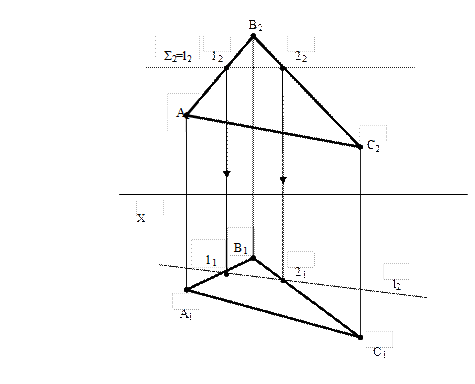Дано: Q(∆ABC), Σ Найти: l=Q ∩ Σ Решение: 1. Σ₂ = l₂ (плоскость частного положения. След-проекция обладает собирательным свойством) 2. l₂ ∩ A₂B₂= 1₂↓1₁ 3. l₂ ∩ B₂C₂= 2₂↓2₁ 4. 1₁ U 2₁= 1₁2₁

Пересечение прямой с плоскостью

Пересечение прямой с плоскостью – точка. Для ее определения необходимо: 1. Через прямую провести вспомогательную плоскость (чаще всего плоскость частного положения) 2. Определить линию пересечения заданной плоскости со вспомогательной плоскостью 3. Определить точку пересечения заданной прямой с найденной линией пресечения двух плоскостей. 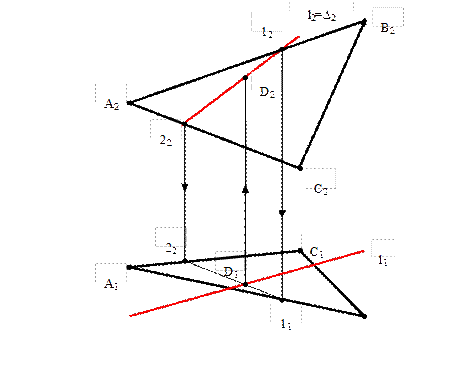  Дано: Σ (∆ABC), l Найти: D=l ∩ Σ Решение: 1. l₂ є ∆₂; ∆ _┴ П₂ 2. Σ₂ ∩ ∆₂ = 1₂2₂1₁2₁ 3. 1₁2₁ ∩ l₂ = D₂     Частные случаи пересечения прямой с плоскостью, когда один (оба) из геометрических образов занимает проецирующее положение. 1. Прямая и плоскость занимают произвольное положение. 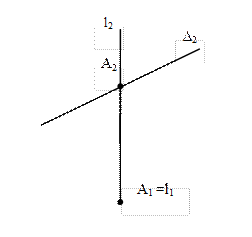  Дано: ∆, l Найти: A=l ∩ ∆ Решение: 1. A₂=l₂ ∩ ∆₂ 2. A₁=l₁     2. Прямая занимает проецирующее положение, плоскость общее. 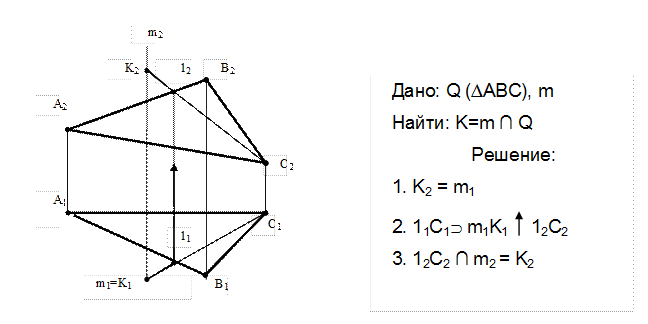3. Плоскость занимает проецирующее положение, прямая общее. 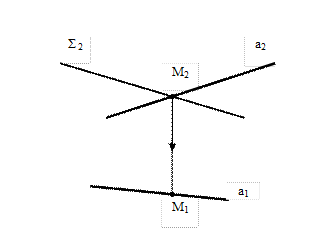Дано: Σ₁, a Найти: M=a ∩ Σ Решение: 1. M₂=a₂ ∩ Σ₂ 2. M₂↓M₁

Вопросы для самоконтроля

1. Какое взаимное положение могут занимать две плоскости, прямая и плоскость в пространстве?

2. Как установить взаимное положение прямой и плоскости?

3. Дайте определение двум параллельным плоскостям.

4. Когда прямая параллельна плоскости?

5. Как провести прямую, параллельную заданной плоскости?

6. Как провести плоскость, параллельную заданной прямой?

7. Как провести через точку плоскость, параллельную заданной плоскости?

8. Как найти линию пересечения прямой с плоскостью?

9. Как определить «видимость» при пересечении прямой с плоскостью?

10. В чем заключается общий способ построения линии пересечения двух плоскостей?

11. Какому условию должны удовлетворять две пересекающиеся плоскости?

Дата добавления: 2014-01-03