
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Лекция № 2
|
|
|
|
Тема: БИНАРНЫЕ ОТНОШЕНИЯ
Основные вопросы, рассматриваемые на лекции:
1. Декартово произведение множеств.
2. Бинарные отношения.
3. Обратное отношение. Композиция отношений.
4. Отношение эквивалентности и фактор-множество.
5. Отношения порядка.
Краткое содержание лекционного материала
1. Декартово произведение множеств. Упорядоченная пара 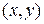 – это объект, в котором указаны первый и второй элементы (соответственно,
– это объект, в котором указаны первый и второй элементы (соответственно, 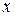 и
и 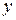 ).
).
Декартовым произведением 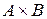 двух множеств
двух множеств 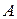 и
и 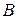 называется множество всех упорядоченных пар с первым элементом из множества
называется множество всех упорядоченных пар с первым элементом из множества 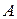 и со вторым элементом из множества
и со вторым элементом из множества 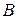 :
:
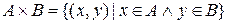 .
.
Если 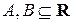 , то декартово произведение
, то декартово произведение 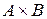 представляется на координатной плоскости: пара
представляется на координатной плоскости: пара 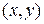 изображается точкой с координатами
изображается точкой с координатами 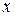 и
и 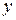 .
.
2. Бинарные отношения. Любое подмножество 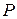 декартова произведения
декартова произведения 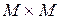 называется (бинарным) отношением на множестве M.
называется (бинарным) отношением на множестве M.
Пусть 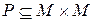 и
и 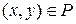 . Тогда пишут
. Тогда пишут 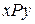 .
.
Приведем основные свойства отношения P, заданного на множестве M:
рефлексивность: для всех x Î M выполняется xPx;
антирефлексивность: для всех x Î M неверно, что xPx;
симметричность: для всех x, y Î M из xPy следует, что yPx;
асимметричность: для всех x, y Î M из xPy следует неверно, что yPx;
антисимметричность: для всех x, y Î M из xPy и yPx следует, что x = y;
транзитивность: для всех x, y, z Î M из xPy и yPz следует, что xPz;
связность: для всех x, y Î M верно, что xPy, или yPz или x = y.
3. Обратное отношение. Композиция отношений. Над отношениями, заданными на множестве M, можно производить те же операции, что над множествами: объединение 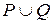 , пересечение
, пересечение 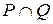 , дополнение
, дополнение 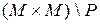 .
.
Отношение 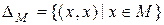 называется диагональю множества M.
называется диагональю множества M.
Отношение 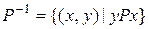 называется обратным к отношению
называется обратным к отношению 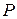 .
.
Отношение 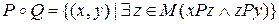 называется композицией отношений
называется композицией отношений 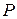 и
и 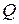 .
.
С помощью операций над отношениями можно охарактеризовать свойства отношений: отношение P на множестве M
рефлексивно тогда и только тогда, когда 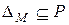 ;
;
антирефлексивно тогда и только тогда, когда 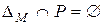 ;
;
симметрично тогда и только тогда, когда 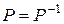 ;
;
асимметрично тогда и только тогда, когда 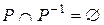 ;
;
антисимметрично тогда и только тогда, когда 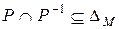 ;
;
транзитивно тогда и только тогда, когда 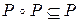 ;
;
связно тогда и только тогда, когда 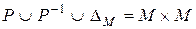 .
.
3. Отношение эквивалентности и фактор-множество. Рефлексивное, симметричное и транзитивное отношение называется эквивалентностью.
Пусть ~ есть эквивалентность на множестве M, а x Î M. Тогда множество [ x ]={ y | y ~ x } называется классом эквивалентности, порожденным элементом x.
Фактор-множество множества 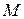 относительно эквивалентности ~ – это семейство всех классов эквивалентности: M /~={[ x ]| x Î M }.
относительно эквивалентности ~ – это семейство всех классов эквивалентности: M /~={[ x ]| x Î M }.
Семейство множеств Mi, i Î I, называется разбиением M на классы, если:
1) для всех i Î I множество Mi непустое подмножество M: Mi ¹Æ, Mi Í M;
2) множества Mi попарно не пересекаются: Mi Ç Mj =Æ, где i ¹ j;
3) объединение всех Mi, i Î I, совпадает с множеством M.
Теорема 1. Пусть на множестве M задана эквивалентность ~. Тогда семейство всех классов эквивалентности [ x ], x Î M, есть разбиение M на классы.
Теорема 2. Пусть дано разбиение M на классы. Тогда отношение P на M, такое, что xPy Û" x и y принадлежат одному классу" есть эквивалентность.
Пример. Разбиение множества всех учеников школы на классы определяет эквивалентность "ученики x и y учатся в одном классе".
5. Отношения порядка. Асимметричное и транзитивное отношение называется порядком. Если порядок является также рефлексивным (антирефлексивным), то называется нестрогим (строгим) порядком. Связный порядок называется линейным. Примеры строгих порядков: <, > на множестве R, Ì, É на множестве 2 M, где M – некоторое множество. Примеры нестрогих порядков: £, ³ на множестве R, Í, Ê на множестве 2 M. Порядки <, >, £, ³ являются линейными, а порядки Ì, É,Í, Ê – нелинейными. Отношение «x делится на y» является нелинейным нестрогим порядком на множестве N, но не на множестве Z. Лексикографический порядок (Расположение слов по алфавиту) является линейным строгим порядком на множество слов некоторого алфавита.
|
|
|
|
|
Дата добавления: 2014-01-03; Просмотров: 346; Нарушение авторских прав?; Мы поможем в написании вашей работы!