Лекция № 1. Для направления 230700.62 Прикладная информатика

КОНСПЕКТ ЛЕКЦИЙ

Дискретная математика

Для направления 230700.62 Прикладная информатика

Профиль " Прикладная информатика в образовании "

Ведущий лектор:

Вахитов Р.Х, доцент, кандидат физико-математических наук, доцент

Воронеж

200__

Тема: Элементы теории множеств

Основные вопросы, рассматриваемые на лекции:

1. Конечные множества.

2. Операции над множествами.

3. Диаграммы Эйлера – Венна.

4. Отношения между множествами.

5. Теорема о числе подмножеств конечного множества.

Краткое содержание лекционного материала

1. Конечные множества. Множество 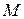называется конечным, если оно пустое или может быть задано перечислением элементов в виде конечной последовательности: 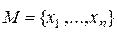. Множество, заданное перечислением элементов, не зависит от того, повторяются элементы или нет, и не зависит от того, переставляются элементы или нет. Например, , .

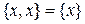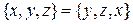Множество 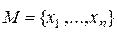называется -множеством, если все элементы 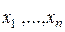попарно различны. Число при этом называется числом элементов (или мощностью) множества 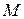и обозначается 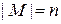. Число элементов пустого множества равно нулю: 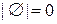. Если множество не конечное, то оно называется бесконечным. Понятие мощности множества обобщается и на бесконечные множества. Мощности бесконечных множеств могут быть различными, например, множества 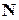и 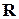имеют различные мощности.

2. Операции над множествами. Перечислим известные четыре бинарные операции и одну унарную операцию над множествами.

Объединением двух множеств 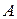и 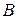называется множество всех элементов, принадлежащих хотя бы одному из множеств 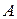и :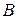

.

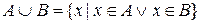Пересечением двух множеств 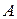и 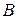называется множество всех элементов, принадлежащих одновременно каждому из множеств 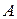и :

.

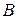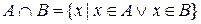Разностью множеств 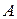и 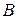называется множество всех элементов, принадлежащих множеству 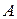, но не принадлежащих множеству :

.

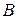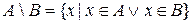Симметрической разностью множеств 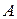и 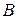называется объединение двух разносте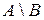й и :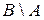

.

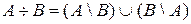Универсальное множество – это множество всех исследуемых объектов.

Дополнением множества 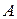называется разность универсального множества 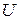и множества :

.

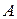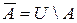3. Диаграммы Эйлера – Венна. Свойства отношений между множествами и операций над множествами можно наглядно проиллюстрировать с помощью диаграмм Венна (или кругов Эйлера). Каждое данное множество изображается в виде круга. Универсальное множество изображается в виде прямоугольника.

Результаты операций выделяются в виде частей круга и их соединений.

4. Отношения между множествами. Перечислим известные четыре бинарных отношения между множествами.

Два множества 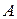и 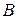называются равными 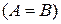, если

.

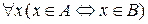Множество 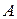называется подмножеством множества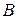 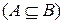, если

.

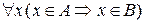Множество 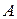называется собственным подмножеством множества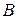 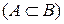, есл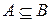и и .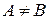

Говорят, что множества 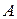и 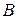не пересекаются, если .

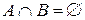5. Теорема о числе подмножеств конечного множества. Существует множество, содержащее все подмножества данного множества 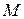. Оно называется множеством всех подмножеств множества 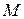и обозначается :

.

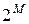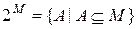Примеры. Если 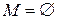, то 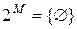. Если 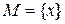, то .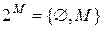

Теорема 1. Пусть множество 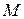конечно. Тогда .

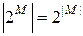Доказательство. Применим математическую индукцию по числу 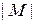элементов множества 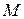. Заметим, что .

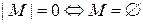База индукции: 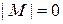. Тогда 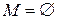, и .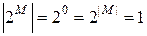

Шаг индукции: допустим, что 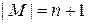, и для всех множеств с элементами утверждение теоремы 1 выполнено. Так как 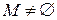, можно выбрать некоторый элемент 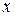множества 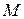. Поскольку 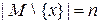, то по индуктивному предположению множество 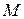имеет 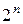подмножеств, не содержащих элемента 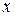. Столько же у него подмножеств, содержащих элемент 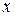. Следовательно, 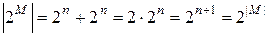. Теорема 1 доказана.

Дата добавления: 2014-01-03