Уравнение первого закона термодинамики для потока

В теплотехнической практике часто приходится иметь дело с процессами, имеющими место при прохождении потока рабочего тела через какой-либо теплотехнический аппарат. Сюда относятся процессы в различных двигателях (например, в паровых или газовых турбинах), в нагнетателях (например, в вентиляторах, дымососах, компрессорах), в каналах переменного сечения – соплах и диффузорах и, наконец, в различных теплообменниках.

Во всех этих случаях процессы протекают с конечными и иногда весьма высокими скоростями. Это противоречит условию обратимости, согласно которому процессы должны протекать бесконечно медленно. Тем не менее при термодинамическом исследовании потока принято считать, что в каждом его сечении рабочее тело находится в равновесном и не изменяющемся во времени состоянии, следовательно, переход тела из одного сечения в другое, бесконечно близкое к нему сечение, одновременно является переходом его из одного равновесного состояния в другое, бесконечно близкое к нему равновесное состояние. При таком условии процессы, протекающие при бесконечно малой разности температур, без трения и тепловых потерь, можно считать обратимыми.

Вначале рассмотрим наиболее общий случай, представленный схематически на рис. 9.1. Предположим, что поток рабочего тела поступает в какой-либо теплотехнический аппарат через входной канал с параметрами 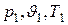и скоростью ω₁ на геометрической высоте Н₁ от условного уровня отсчета. В самом аппарате рабочее тело получает от внешнего источника теплоту q и совершает над внешним объектом работу l_Т, а затем покидает аппарат через выходной канал с параметрами 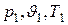и скоростью ω ₂ на высоте Н₂ от того же уровня отсчета.

В аппарате протекает обратимый процесс, при котором внутренняя энергия рабочего тела изменяется на величину 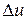и совершается работа изменения объема l, причем по первому закону

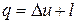. (9.1)

Это выражение, относящееся к процессу в потоке, можно представить в другом виде на основе следующих соображений.

Работа изменения объема расходуется в четырех различных направлениях. Часть ее, называемая работой проталкивания l_п,затрачивается на преодоление действия внешних сил; другая часть, называемая технической работой l _т, совершается, как было сказано выше, над внешним объектом; третья часть обозначаемая l_к, затрачивается на изменение внешней кинетической энергии потока; наконец, четвертая часть её обозначаемая через l_пот, затрачивается на изменение внешней потенциальной энергии потока, связанное с изменением его геометрической высоты. Таким образом, уравнение первого закона термодинамики для потока в общем случае принимает вид

. (9.1^/)

Определим работу потока против внешних сил. Для этого представим себе, что поток, проходящий через аппарат, отделен от остальной части его слева и справа условными невесомыми пластинками П₁ и П₂. Тогда на пластинку П₁ будет действовать внешняя сила p₁f₁, а на пластинку П₂ – внешняя сила p₂f₂, где f₁ и f₂ – площади сечения входного и выходного каналов.

За то время, пока через аппарат проходит 1кг рабочего тела, пластинка П₁ смещается вправо на расстояние s₁, а пластинка П₂ – тоже вправо на расстояние s₂. Это означает, что между начальным и конечным положениями пластинок помещается 1 кг рабочего тела, следовательно, .

Работа перемещения пластинки П₂ на расстояние s₂, равная и называемая работой выталкивания (поскольку она затрачивается на выталкивание 1кг рабочего тела из аппарата), совершается рабочим телом против внешней силы p₂f₂, следовательно, математически она положительна. Наоборот, работа перемещения пластинки П₁ на расстояние s₁, равная и называемая работой вталкивания (поскольку она затрачивается на вталкивание 1 кг рабочего тела в аппарат), совершается внешней силой p₁f₁ над рабочим телом, следовательно, математически она отрицательна.

Таким образом, суммарная работа потока против внешних сил, т. е. работа проталкивания, составляет

. (9.2)

Кинетическая энергия тела, обладающего массой М, кг, определяется его скоростью ω, м/сек, согласно известному из механики соотношению составляет М ω²/2, Дж, а применительно к 1 кг рабочего тела она равна

ω²/2, Дж/кг. Поэтому работа, затраченная на изменение внешней кинетической энергии потока в аппарате, составляет

. (9.3)

Вес тела, обладающего массой М, кг, составляет М g, Н, где g, м/сек²– ускорение свободного падения, а применительно к массе в 1 кг он равен g, Н/кг. Поэтому внешняя потенциальная энергия тела с массой 1 кг, находящегося на геометрической высоте Н, равна gН, Дж/кг, а работа, затраченная на изменение потенциальной энергии потока в аппарате, составляет

. (9.4)

В связи с этим уравнение первого закона термодинамики для потока в развернутой форме принимает вид

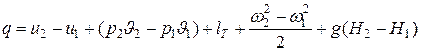. (9.5)

Учитывая, что сумма представляет собой энтальпию рабочего тела i и, следовательно,

,

общее уравнение первого закона термодинамики для потока можно представить и в таком виде

. (9.6)

Сопоставив эту форму уравнения первого закона термодинамики для потока с другой его формой

, (9.7)

которая легко получается из исходного уравнения (9.1), совершенно аналогично тому, как это было выполнено в п 1.6 для процесса изменения состояния неподвижного рабочего тела, получаем

. (9.8)

В 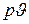– диаграмме рассмотренного процесса (рис. 9.2) интеграл правой части этого уравнения изображается площадью 1-2-3-4-1, которая, таким образом, представляет собой часть работы изменения объема рабочего тела, могущую быть полезно использованной на совершение технической работы и на изменение внешней энергии потока, а потому часто называемую располагаемой работой (остальная часть, равная роботе проталкивания, как очевидно, полезно использованной быть не может).

Изложенное показывает, что в уравнении (9.7.), полученном для потока, интеграл в правой части имеет вполне конкретный физический смысл. Вместе с тем, как уже было отмечено в п 1.6, в совершенно аналогичном по форме уравнении для неподвижного рабочего тела он лишен такого физического содержания и представляет собой просто абстрактную математическую величину.

В, этом легко убедиться, рассмотрев, например, изохорное охлаждение рабочего тела в каком-либо сосуде с постоянным объемом (рис. 9.3). Действительно, в этом случае

,

т. е. указанный интеграл нулю не равен, хотя никакой работы газом не совершается и изменения его внешней энергии не происходит.

В связи с этим, рассматривая какой-либо процесс в 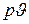– диаграмме, непременно следует уточнить, находится ли рабочее тело в неподвижном состоянии или в движении.

Дата добавления: 2014-01-03