Истечение газов через суживающиеся сопла

Поскольку назначением сопла является преобразование потенциальной энергии рабочего тела в кинетическую, для анализа происходящего в нем процесса начальная скорость потока является несущественной и можно принять ω₁ =0. Тогда уравнение первого закона термодинамики при адиабатном истечении рабочего тела через сопло принимает вид

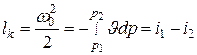, (9.21)

где ω ₀ – теоретическая скорость, потока в выходном сечении сопла;

p₁ – начальное давление рабочего тела;

р₂. – давление среды, в которую, происходит истечение.

Как видно из закона геометрического обращения воздействия, это уравнение справедливо для суживающихся сопл в таком диапазоне давлений, при котором скорость истечения остается меньшей, чем местная скорость звука в выходном сечении сопла, или, в крайнем случае, достигает ее.

Разность энтальпий i₁-i₂ при истечении через сопла также называется располагаемым теплопадением: и обозначается через h₀. 0на соответствует тому максимуму кинетической энергии, который может быть получен лишь в идеальных условиях истечения, а фактически из-за неизбежных потерь, связанных с необратимостью процесса, никогда не достигается.

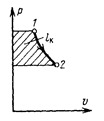Как и техническая работа адиабатного потока в идеальном двигателе (когда ω₁ = ω₂ =0), располагаемое теплопадение в данном случае (когда l _T=0) изображается в pυ – диаграмме площадью, расположенной между линией адиабатного расширения тела в сопле 1-2 и осью ординат (рис. 9.11).

Исходя из равенства 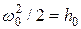, теоретическую скорость истечения рабочего тела через сопло в рассматриваемом случае можно определить по формуле

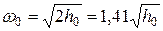
, м/сек. (9.22)

Здесь h₀ выражено в Дж/кг. Если его выразить в кДж/кг, то формула принимает вид

, м/сек (9.23)

Это соотношение справедливо для любого рабочего тела. Ограничиваясь же рассмотрением идеальных газов, подчиняющихся уравнению состояния (2.3) и всем вытекающим из него закономерностям, мы получаем формулу для теоретической скорости истечения в ином виде. В самом деле

,

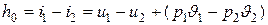а поскольку для идеального газа при адиабатном процессе

,

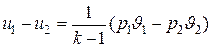о получаем

.

Тогда

.

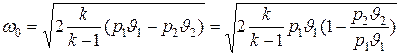Основной характеристикой процесса истечения является отношение конечного давления к начальному, т.е. величина

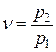. (9.25)

Выразим теоретическую скорость истечения ω₀ как функцию величины ν. Для этого выполним следующие преобразования

.

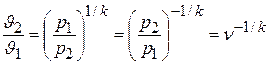
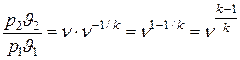Тогда

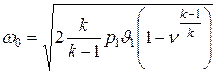, м/сек (9.26)

Обозначив площадь выходного сечения канала через f₂, в соответствии с (9.16) получим

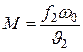, кг/сек, (9.27)

или

.

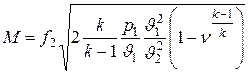Далее

,

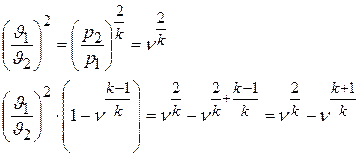тогда

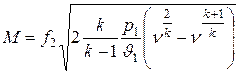, кг/сек (9.28)

Анализ данного выражения показывает, что при 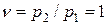, т.е. когда р₂ = р₁, расход газа М = 0, т.е. истечение газа не происходит. При уменьшении ν расход газа возрастает, но при ν = 0 он опять становится нулевым.

Математически это объясняется тем, что при р₂ = 0, удельный объем газа 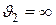, скорость же истечения остается конечной. Действительно, если в формулу (9.26) подставить ν = 0, то получим

.

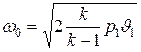Очевидно, что сопло ограниченного сечения не может пропустить с конечной скоростью газ, имеющий бесконечно большой удельный объем. Из формулы (9.27) для этого случая получаем М = 0.

Из сказанного вытекает, что при некотором значении расход газа М достигает максимума. Чтобы найти значение ν, соответствующее этому максимуму, следует приравнять нулю первую производную функции

,

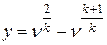т.е.

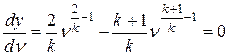
или

.

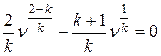Для решения этого уравнения относительно ν разделим его на величину

,

после чего получим

или, после сокращения

откуда

.

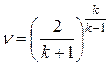Значение ν, при котором расход газа достигает максимума, называется критическим и обозначается через ν_кр. Таким образом,

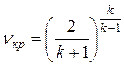. (9.29)

Как и показатель адиабаты, величина ν_кр является физической константой газа, т.е. одной из характеристик его физических свойств.

В действительности после достижения максимума расхода газа с уменьшением ν не уменьшается, как это вытекает из формулы (9.28), а остается постоянным (рис. 9.12). Физическое объяснение этому дано ниже.

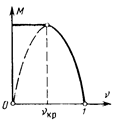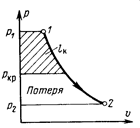
Данный анализ показывает, что при уменьшении давления газа за соплом р₂. (при неизменном давлении p₁) расход газа сначала увеличивается, а затем, когда за соплом устанавливается критическое давление , увеличение расхода газа прекращается и, как бы ни уменьшалось давление р₂, в выходном сечении будет иметь место постоянное давление р_кр. Расширение газа, связанное с понижением давления от р_кр до р₂, будет происходить уже вне сопла и потому не дает дополнительного возрастания скорости. Освобождающаяся при этом энергия будет затрачиваться на завихрения вокруг газовой струи.

Таким образом, если , то при истечении газа из суживающегося сопла имеет место потеря энергии, бесполезно рассеиваемой в пространстве за соплом. Нетрудно видеть, что эта потеря в 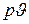–диаграмме (рис. 9.13) при расширении газа по линии 1-2 изображается площадью, расположенной под изобарой р_кр, кинетическая же энергия выходящей из сопла струи изображается заштрихованной площадью над этой изобарой.

Соответствующая этому случаю скорость истечения называется критической скоростью. Значение ее можно получить из формулы (9.26)

.

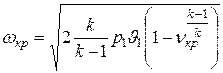Подставим сюда значение ν_кр из формулы (9.29), выполнив одновременно следующие преобразования

Тогда получим

, м/сек.

Найдем зависимость между величиной ω_кр и параметрами газа

в выходном сечении р_кр и υ_кр, выразив через них произведение .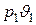

При адиабатном истечении

Тогда

и

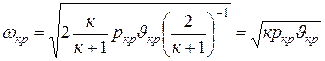. (9.30)

Полученная формула показывает, что критическая скорость истечения газа из сопла равна скорости распространения звуковой волны в этом газе при его параметрах р_кр и υ_кр, т. е. местной скорости звука в выходном сечении сопла.

В этом содержится физическое объяснение тому, что при снижении внешнего давления р₂ ниже р_кр, скорость истечения не изменяется, а остается равной ω_кр.

Действительно, если р₂ > р_кр, то ω < ω_кр или ω < а и всякое понижение давления р₂ передается вдоль сопля в направлении, обратном движению потока, со скоростью а- ω. При этом происходит перераспределение давлений и скоростей по всей длине сопла: в каждом промежуточном сечении устанавливается новая скорость, соответствующая большему расходу газа. Если же р₂ снизится до p_{к р}, то дальнейшее понижение его уже не сможет распространяться вдоль сопла, поскольку скорость его распространения навстречу потоку снизится до нуля (а- ω_кр= 0). Поэтому в промежуточных сечениях сопля расход газа не изменится, не изменится он и в выходном сечении, т. е. скорость истечения останется постоянной и равной ω_кр.

Дата добавления: 2014-01-03