Модуль 3

Комплексная цель модуля: освоение вычислительных алгоритмов, основанных на результатах линейной алгебры.

Содержание модуля: методы решения систем линейных уравнений, проблемы собственных чисел матрицы.

§6. Вычислительные методы линейной алгебры

6.1. Вычислительные методы линейной алгебры. Этот параграф предваряет обширную группу методов, в которых используются результаты и подходы фундаментальной для вычислителя дисциплины - линейной алгебры. К таким методам относят методы решения систем линейных алгебраических уравнений (СЛАУ), нахождения собственных значений и собственных векторов матриц, нулей многочлена и др.

В зависимости от структуры, размера, характера конкретной задачи для её решения могут применяться методы, которые качественно отличаются друг от друга: это методы точные, итерационные и вероятностные. Дадим, следующие определения.

Определение 6.1. Метод решения задачи относят к точным, если его применение приводит к точному решению за конечное число шагов.

Определение 6.2. Метод является итерационным, если при его применении приближённое решение стремится к точному и сливается с ним за бесконечное число шагов.

Как видно из названия, к вероятностным методам относятся те, в которых используются результаты теории вероятностей.

Определение 6.3. Под вероятностными методами понимается совокупность приёмов решения задачи при помощи многократных случайных испытаний (такие методы часто называются методами Монте-Карло).

Нельзя однозначно утверждать, что только размер задачи имеет значение при выборе того или иного класса методов. Например, при решении СЛАУ, матрица которой имеет треугольную структуру, независимо от размера задачи удобно применять метод прогонки (см. § 7). Конечно, если речь идёт о задаче общего вида, не имеющей никаких особых отличий, то, как правило, для задач с «малым» числом неизвестных применяют точные методы, для задач со «средним» числом неизвестных применяют итерационные методы, для задач с «большим» числом неизвестных применяют вероятностные методы. С развитием вычислительной техники задачи из одного класса переходят в другой, но вряд ли когда-либо полностью отомрут представители одного из трёх вышеназванных групп методов.

6.2. Нормы векторов и матриц и их согласованность. При применении итерационных методов требуется иметь возможность на каждом шаге метода определять, как близко приближённое решение «подошло» к искомому точному. Когда речь идёт о решении СЛАУ, то термин «приближённое решение» относится к набору величин – вектору решений СЛАУ. Таким образом, следует уметь вычислять «расстояние» между векторами, находить «величину» соответствующего вектора. Но при решении СЛАУ вектора взаимодействуют с матрицами. Следовательно, требуется уметь вычислять и «величину» соответствующей матрицы. Интуитивно понятно, также, что определения метрических свойств векторов и матриц должны быть согласованы между собой. Здесь снова используем понятие нормы (в § 2 мы применяли понятие нормы для того, чтобы вычислить «расстояние» между функциями) – нормы вектора и матрицы. Используем определения основных норм в пространствах векторов и матриц [9].

Определение 6.4. Если в пространстве векторов 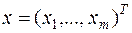введена норма 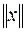, то согласованной с ней нормой в пространстве матриц 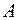называют норму

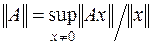
(6.1)

Наиболее употребительны в пространстве векторов следующие нормы:

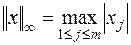
	(6.2)
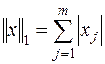
	(6.3)
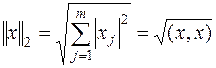
	(6.4)

Утверждается, что согласованными с определениями (6.2)-(6.4) нормами векторов в пространстве матриц являются соответственно нормы

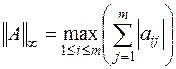
	(6.5)
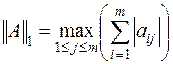
	(6.6)
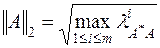
	(6.7)

здесь и далее 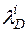- собственные значения матрицы .

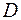Пример 6.1. Дан вектор 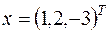(значок 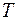означает операцию транспонирования). Найти его нормы, определённые по (6.2), (6.3), (6,4).

Дата добавления: 2014-01-03