Решение. 1) Нормы матрицы найдём по формулам (6.5)-(6.7):

1) Нормы матрицы найдём по формулам (6.5)-(6.7):

, ,

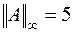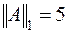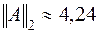
2) Для вычисления числа обусловленности матрицы по формуле (6.27) найдём её обратную матрицу по формул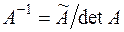е , где 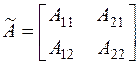, 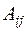- алгебраические дополнения соответствующих элементов матрицы, 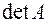- определитель матрицы 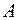. Получим: 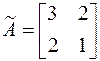, , 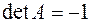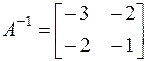. Вычислим 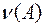по формуле (6.27), используя нормы (6.5) и (6.6):

, , ,

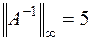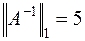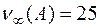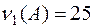
3) Для оценки числа обусловленности по формуле (6.28) найдём собственные числа матрицы 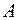: 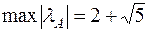, , 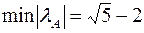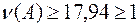. Отметим, что данная оценка соответствует точному значению .

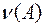Пример 6.4. Оценить абсолютную погрешность решения СЛАУ 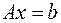, если известно, что матрица 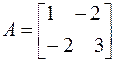задана точно, а правая часть – с погрешностью .

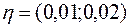Решение. Для оценки воспользуемся формулой (6.21). Значения норм матрицы возьмём из предыдущего примера. Подсчитаем нормы вектора 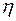, применяя формулы (6.2) и (6.3): , ; , .

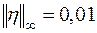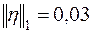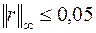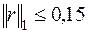6.4. Вычислительная практика. Вычисление норм векторов и матриц средствами пакета MAPLE.

Рекомендуемая литература: [18].

При работе в пакете Maple с матрицами и векторами необходимо использовать библиотеку linalg, которая подключается с помощью with(linalg); (если после оператора стоит «;», то выдается сообщение обо всех функциях содержащихся в библиотеке, если после оператора стоит «:», сообщение не выдается). Определить матрицу и вектор можно с помощью операторов:

1. 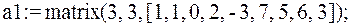– здесь первые два индекса указывают на число строк и столбцов матрицы 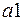, далее в квадратных скобках перечисляются через запятую все элементы матрицы;

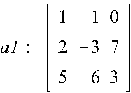
Для вектора: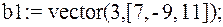

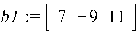
2. 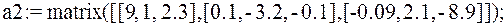– матрица задается списком строк (по строкам):

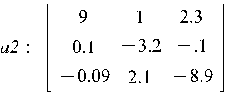
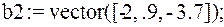
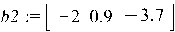
3. 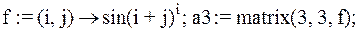– матрица может быть задана с помощью функции, определяющей ее элементы

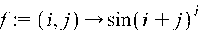
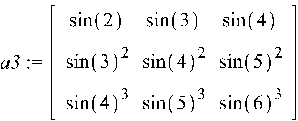
4. если матрица (вектор) имеет нулевые элементы: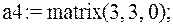

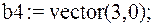
5. 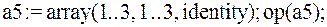– задание единичной матрицы, оператор op служит для отображения матриц (векторов):

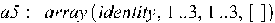
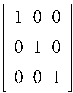
6. описание матрицы (вектора) 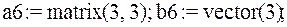– указывается число строк и столбцов для матриц и число элементов для вектора:

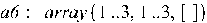
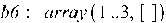
7. транспонированную матрицу можно получить с помощью оператора transpose: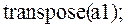

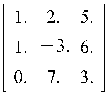
8. для нахождения обратной матрицы используют оператор inverse: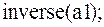

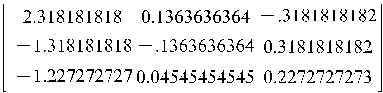
В Maple используют следующие нормы:

Нормы векторов:

№	Формула	Представление в Maple

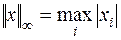
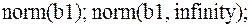
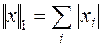
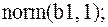
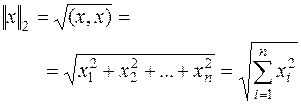
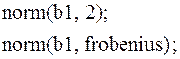
Найдем все нормы для вектора :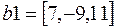

1. 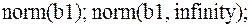ответ: 11;

2. 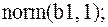ответ: 27;

3. 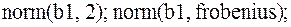ответ: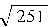

Нормы матриц:

№	Формула	Представление в Maple
	Строковая норма:
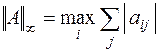
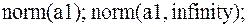
	Столбцовая норма:
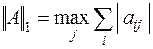
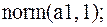
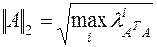
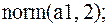
	Норма Фробениуса

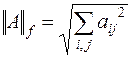
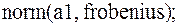
Здесь 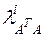– 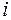-ое собственное значение матрицы .

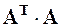Найдем все нормы для матрицы :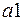

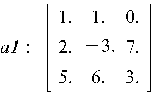
1. 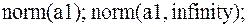ответ: 14;

2. 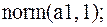ответ: 10;

3. 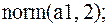ответ: 8.971690045;

4. 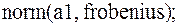ответ: 11.57583690;

Замечание: Если матрица 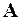симметрична (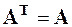), то 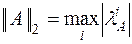, или в более общей формулировке любая норма симметричной матрицы не меньше максимального из ее собственных значений .

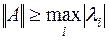Число обусловленности матрицы

Число обусловленности матрицы определяется формулой (6.27)

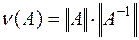
причем нормы должны быть согласованы, т.е. если в 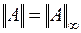, то и для вычисления нормы обратной матрицы следует взять 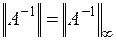. Для числа обусловленности матрицы справедлива оценка (6.28):

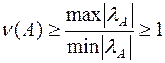
Отметим такое важное применение нормы матрицы, как определение погрешности решения системы линейных алгебраических уравнений (СЛАУ) 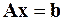по заданной погрешности правой части .

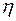Погрешность решения СЛАУ 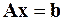при заданной погрешности правых частей может быть оценена до решения системы по формуле (6.21):

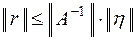
В практических занятиях часто возникает необходимость вычисления обратных матриц. Для квадратных матриц размерности 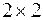справедлива теорема: Если матрица 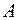принадлежит 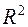, то и обратная матрица 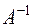принадлежит 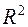и определяется формулой (частный случай формулы, приведённой в примере (6.3)):

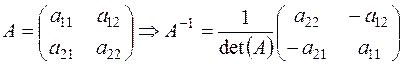
Дата добавления: 2014-01-03