Метод прогонки решения системы линейных алгебраических уравнений

7.1. Постановка задачи. Прямой и обратный ход прогонки. Данный метод относится к классу точных методов (в соответствии сопределением, сформулированным в предыдущем параграфе). Решается СЛАУ

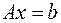(7.1)

в частном случае, когда матрица 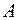является трехдиагональной, т.е. все элементы такой матрицы, не лежащие на главной и двух побочных диагоналях, равны нулю. Такую СЛАУ можно записать в виде

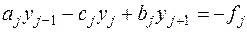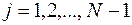, (7.2)

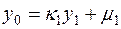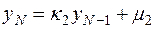, (7.3)

Соотношения (7.2), (7.3) представляют собой систему из 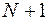уравнения относительно 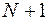неизвестного 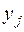. Распишем матрицу коэффициентов данной системы, чтобы визуально убедиться в её трехдиагональности:

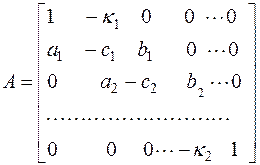
Следуя [19], решение системы (7.2) будем искать в виде

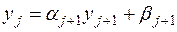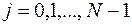, (7.4)

где 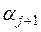, 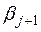- неизвестные пока коэффициенты. Подставляя в (7.4) 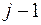вместо 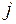, получим:

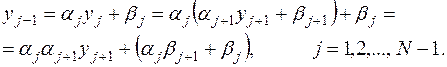(7.5)

Подставляя (7.4), (7.5) в уравнение (7.2), приходим при 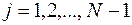к уравнению

.

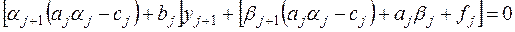Последнее уравнение будет выполнено, если коэффициенты 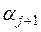, 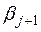выбрать такими, чтобы выражения в квадратных скобках обращались в нуль. Отсюда находим выражения для искомых коэффициентов:

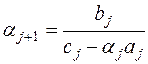
	(7.6)

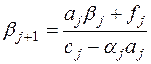
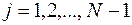
Получены рекуррентные соотношения: для того, чтобы по этим формулам начать последовательно вычислять коэффициенты 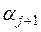, , 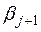необходимо иметь значения 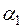, 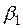. Для того, чтобы их найти, потребуем чтобы соотношение (7.4) при 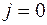было эквивалентно первому из равенств (7.3). Имеем:

,

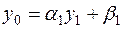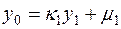
Отсюда получаем

,

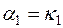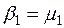
(7.7)

Процесс нахождения коэффициентов 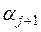, 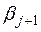по формулам (7.7), (7.6) называется прямой прогонкой. После того как прогоночные коэффициенты 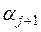, ,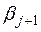, 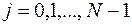найдены, решение системы (7.2), (7.3) находится по рекуррентной формуле (7.4), начиная с 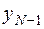и вплоть до 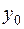. Но для начала счета по этой формуле требуется знать 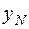, которое определяется как решение системы двух уравнений: второго из уравнений (7.3) и уравнения (7.4), взятого при :

,

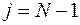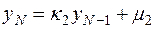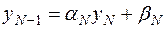
(7.8)

Решая систему (7.8), находим:

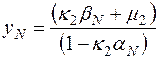
(7.9)

Теперь оставшиеся неизвестные можно вычислить, применяя (7.4) в обратном порядке:

,

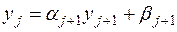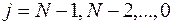
(7.10)

Нахождение 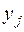по формулам (7.9) и (7.10) называется обратной прогонкой.

Рассмотрим Пример 7.1. Методом прогонки решить систему уравнений: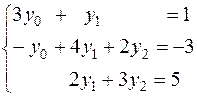

Решение. Сопоставляя данную систему с канонической системой (7.2), (7.3), замечаем, что в нашем примере 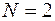и коэффициенты системы (7.2), (7.3) для нашего примера имеют следующие значения:

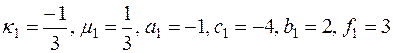
Прямой ход метода прогонки: по формулам (7.7) вычисляем 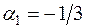, 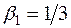; по формулам (7.6) находим , .

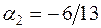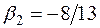Обратный ход метода прогонки: по формуле (7.9) вычисляем 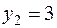; по формулам (7.10) находим , .

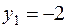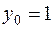7.2. Достаточные условия возможности применения метода. Очевидно, формулы (7.6), (7.9) можно использовать, если в них знаменатели не обращаются в нуль. Докажем, что для возможности применения метода прогонки достаточно потребовать выполнения условий ( назовём их соотношениями А):

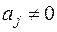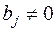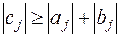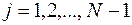
, , ,	(7.11)
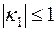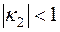
,	(7.12)

Вначале докажем при помощи метода математической индукции, что все коэффициенты 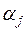, , 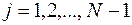не превосходят единицы. В самом деле, из (7.7) и (7.12) следует, что 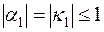. Пусть, теперь, для некоторого 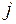имеет место неравенство 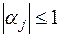. Докажем, что это верно и для 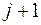, т. е. 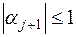. Рассмотрим цепочку очевидных неравенств

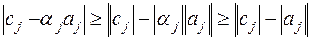
В последнем неравенстве использовано условие 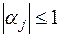. Продолжая эти неравенства с учётом условий (7.11), получаем:

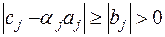
(7.13)

На данном этапе доказательства методом индукции мы попутно обнаружили, что знаменатели выражений (7.6) не обращаются в нуль. Разделим обе части неравенства (7.13) на его левую часть и, с учётом (7.6), получим:

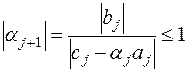
(7.14)

Таким образом, методом математической индукции доказано, что , .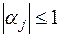

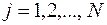Теперь рассмотрим знаменатель выражения из формулы (7.9). Учитывая только что доказанное соотношение 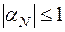и второе условие из (7.12), имеем

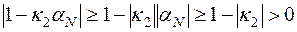
т.е. не обращается в нуль и знаменатель в выражении для 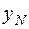. Итак, соотношения А доказаны.

Пример 7.2. Проверьте, удовлетворяют ли условиям (7.11), (7.12) коэффициенты системы из предыдущего примера.

7.3. О вычислительной погрешности метода. Остановимся на вопросе о том, как будет вести себя погрешность, внесенная на каком-либо шаге вычислений в методе прогонки. Сейчас речь идёт о погрешности, которая появляется из-за округлений при вычислениях на компьютере. Пусть, например, в процессе обратной прогонки на шаге 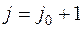вместо 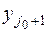вычислена величина 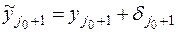. Тогда на следующем шаге, т.е. при 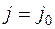, применяя формулу (7.10), вместо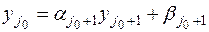получим величину 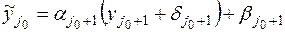и погрешность окажется равной 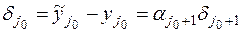. Оценивая это неравенство по модулю, с учётом условия (7.14), получаем, что 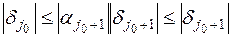, т.е. погрешность не возрастает.

7.4. Упражнения

1.

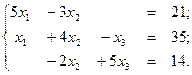
2. ,

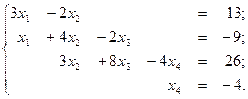3.

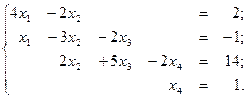
4.

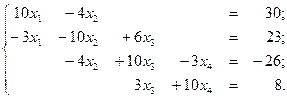
5.

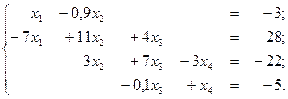
6.

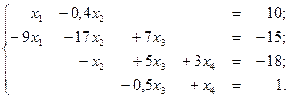
7.

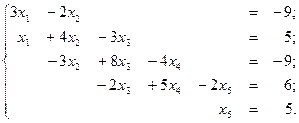
7.5. Вычислительная практика

Задание.

Решить систему алгебраических уравнений вида методом прогонки.

Пример выполнения задачи

Приведем пример нахождения при помощи пакета Maple решения следующей системы уравнений:

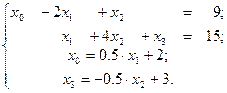
Отметим, что точное решение для данной системы имеет вид:

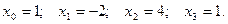
Вначале зададим значения коэффициентов 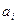, , 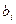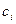и 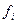(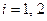), а также значения для 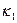, , 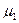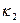и :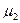

> a1:=1; a2:=1;

b1:=-2; b2:=4;

c1:=1; c2:=1;

f1:=9; f2:=15;

kappa1:=0.5; mu1:=2;

kappa2:=-0.5; mu2:=3;

Далее вычислим все прогоночные коэффициенты (для данного примера их будет шесть: 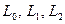и ).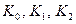

> L0:=kappa1;

K0:=mu1;

L0:=.5

K0:= 2.0

> L1:=-c1/(a1*L0+b1);

K1:=(f1-a1*K0)/(a1*L0+b1);

L1:=.6666666667

K1:= -4.666666667

> L2:=-c2/(a2*L1+b2);

K2:=(f2-a2*K1)/(a2*L1+b2);

L2:= -.2142857143

K2:= 4.214285715

Теперь вычислим значения неизвестных:

> x[3]:=(mu2+K2*kappa2)/(1-kappa2*L2);

x[2]:=L2*x[3]+K2;

x[1]:=L1*x[2]+K1;

x[0]:=L0*x[1]+K0;

x[3]:=.9999999991

x[2]:= 4.000000001

x[1]:= -2.000000000

x[0]:= 1.000000000

Рекомендации к составлению программ и описание параметров функции.

Метод прогонки должен быть реализован процедурой, для которой входными параметрами являются коэффициенты 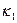, , 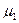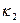и 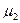, а так же массивы коэффициентов 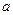, , 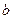, 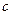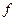и величина 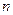. Выходным параметром будет служить массив 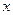, являющийся решением системы линейных алгебраических уравнений.

Массивы прогоночных коэффициентов должны быть описаны внутри процедуры.

Прототип функции в языке С++, реализующей метод прогонки, может быть описан одним из предложенных вариантов.

Вариант 1:

double* Progon3(double*a, double*b, double*c, double*f,

double k1, double k2, double mu1, double mu2);

Вариант 2:

void Progon3(double*a, double*b, double*c, double*f,

double k1, double k2, double mu1, double mu2, double*x);

Варианты заданий ().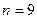

1)

a = (3, 8, -4, -3, 7, 10, -1, 2); b = (9, 15, -15, 8, 11, 12, -3, -4);

c = (-3, -5, 9, 4, 4, 2, -2, 2); f = (-7, 1, -10, 6, 7, 8, -7, -3);

κ₁ = 0.1; μ₁ = -9.0;

κ₂ = -0.8; μ₂ = -2.0;

Ответ:

x = (-8.795937, 2.040630, -0.340714, 2.042867, 2.142240, -1.252329, 1.444985, 1.591735, 0.389905, -2.311924);

2)

a = (-5, -8, 4, -1, -9, 3, 5, -9); b = (15, 14, 9, 13, 22, 15, 7, 10);

c = (-9, -3, -2, 10, 10, 10, -1, -1); f = (7, -5, -2, 2, -3, 6, 2, 7);

κ₁ = 0.0; μ₁ = -7.0;

κ₂ = -0.6; μ₂ = 5.0;

Ответ:

x = (-7.0, -3.029276, -1.937682, 0.702220, 0.284628, 0.099795, 0.175714, 0.366367, 1.443142, 4.134115);

3)

a = (-4, 7, 8, 6, 3, 2, 4, 7); b = (13, -12, 16, -16, 10, -8, -13, -14);

c = (-8, 4, 8, 7, -7, -6, -9, -6); f = (-2, -10, 2, -7, -3, -8, 1, 6);

κ₁ = -0.9; μ₁ = 9.0;

κ₂ = 0.0; μ₂ = -6.0;

Ответ:

x = (6.171998, 3.142225, 2.270117, -1.188542, 0.356967, 0.834675, 1.773951, -0.753709, 1.766003, -6.0);

4)

a = (-5, 5, 6, 2, -6, 3, 10, -5); b = (-8, -11, 12, 12, -15, 11, -22, -18);

c = (-1, 5, -4, 8, 6, -6, -10, 10); f = (-6, 2, 4, 1, 6, -10, -1, -8);

κ₁ = -0.5; μ₁ = 9.0;

κ₂ = -0.7; μ₂ = -5.0;

Ответ:

x = (12.322089, -6.644178, -2.457022, 1.638729, 0.230653, -0.630662, -0.346002, 0.716999, -1.823400, -3.723620);

5)

a = (-3, 4, -7, 9, 7, 3, -5, -5); b = (7, 14, 12, 19, -15, 10, 14, -13);

c = (3, -8, 3, 7, 8, 5, 7, 6); f = (-7, -6, -5, 6, -1, 10, -1, -8);

κ₁ = 0.0; μ₁ = 4.0;

κ₂ = -0.8; μ₂ = 4.0;

Ответ:

x = (4.0, 1.482991, -1.793646, -1.647385, 0.737700, 0.972881, 1.053663, -0.691055, 1.991869, 2.406504);

6)

a = (8, 4, 7, 2, -4, 2, 5, -6); b = (-17, 14, -19, -13, -9, 8, 10, 12);

c = (8, 8, -10, 10, 5, -6, -3, -5); f = (-1, -5, -4, 5, -10, 2, 4, -7);

κ₁ = 0.7; μ₁ = 1.0;

κ₂ = -0.5; μ₂ = -1.0;

Ответ:

x = (1.345971, 0.494245, -0.420701, -0.135895, 0.363710, 1.2, 0.090971, 0.121296, -0.777395, -0.611303);

7)

a = (-4, -1, -3, 7, -10, -7, -9, -8); b = (7, -10, -13, -11, 21, 9, -18, -18);

c = (-1, -7, -8, -4, 8, 1, -6, 9); f = (-8, -8, -1, -8, 1, -3, -2, 10);

κ₁ = 0.6; μ₁ = 8.0;

κ₂ = -0.1; μ₂ = 3.0;

Ответ:

x = (11.192692, 5.321153, 0.477304, -0.299171, 0.432164, 0.288000, 0.090794, -0.166858, 0.970099, 2.902990);

8)

a = (4, -3, -4, -9, 3, 4, 1, -4); b = (-9, -11, -10, 17, 5, -12, 4, -16);

c = (5, 5, 6, 5, 2, 5, 3, -10); f = (3, -1, 2, 2, 10, 9, -7, -6);

κ₁ = -0.8; μ₁ = 1.0;

κ₂ = -0.9; μ₂ = -3.0;

Ответ:

x = (1.055119, 0.068899, -0.368114, -1.051189, -1.664058, 4.165656, -2.918053, -8.535851, 10.020486, -12.018437);

9)

a = (3, 5, -4, 5, -5, -9, -4, -4); b = (-14, 14, 13, 16, -13, -19, -11, -15);

c = (-10, 7, -9, -9, -6, 7, -7, -9); f = (-8, 8, -4, -9, -10, 5, -4, 10);

κ₁ = 0.8; μ₁ = -6.0;

κ₂ = 0.4; μ₂ = -7.0;

Ответ:

x = (-7.493924, -1.867405, 1.166190, 0.144338, 0.134626, 1.319522, -1.304486, -1.129933, 3.092459, -5.763017);

10)

a = (-2, -10, -8, -3, 5, 5, -4, -2); b = (9, 20, 18, -8, 14, -7, 14, -8);

c = (-4, -7, 10, 3, -9, 2, 10, 5); f = (2, -9, -6, -10, -3, -10, -9, -3);

κ₁ = -0.1; μ₁ = -9.0;

κ₂ = 0.8; μ₂ = -6.0;

Ответ:

x = (-8.680337, -3.196631, -3.352251, -3.725530, 3.424154, 2.072213, 5.459084, 8.926260, -11.213130, -14.970504);

11)

a = (6, 3, -9, -4, -2, 6, -8, -2); b = (18, -8, -10, 9, -6, 13, -20, -10);

c = (9, -2, 1, 5, -3, -7, -10, -6); f = (6, -6, 6, -5, 2, -5, -10, -10);

κ₁ = -0.3; μ₁ = 8.0;

κ₂ = 0.1; μ₂ = 6.0;

Ответ:

x = (8.767828, -2.559428, 0.059697, -0.600356, -0.540826, -0.506798, 0.707480, 1.593779, -2.753543, 5.724646);

12)

a = (3, -9, -6, -7, 7, 4, -8, -5); b = (-12, -18, -16, 16, 18, -13, -18, -11);

c = (8, 8, 7, -6, -9, -7, -9, -4); f = (5, -6, -4, 9, 7, -4, 6, 9);

κ₁ = 0.5; μ₁ = 2.0;

κ₂ = 0.3; μ₂ = -2.0;

Ответ:

x = (2.191962, 0.383925, 0.378901, 0.534444, 0.974930, 0.476296, 0.933093, -0.889289, 0.282495, -1.915251);

13)

a = (9, 8, 8, 3, -2, -6, 2, 2); b = (16, -19, 11, 13, -3, -8, 10, 7);

c = (-5, 9, -1, 7, -1, 2, -5, -5); f = (8, -4, -6, 2, -6, 9, -8, -5);

κ₁ = 0.6; μ₁ = 1.0;

κ₂ = -0.1; μ₂ = 2.0;

Ответ:

x = (0.951677, 0.080539, -0.144706, -0.678345, -2.619446, 5.441120, -5.084466, 0.485494, 0.537202, 1.946280);

14)

a = (2, -1, -3, -4, 9, 7, 10, 5); b = (-7, -11, -11, 10, -16, -14, 16, 12);

c = (-2, 9, -7, -3, -6, -5, 5, -6); f = (-6, -1, 1, -3, 9, 6, 3, -8);

κ₁ = -0.3; μ₁ = -5.0;

κ₂ = 0.7; μ₂ = 9.0;

Ответ:

x = (-4.821432, -0.595227, 0.261863, 0.142807, -0.479495, -0.788727, -0.115970, -1.979502, 7.166348, 14.016443);

15)

a = (1, -7, -9, -4, -8, -7, 1, 1); b = (-11, -10, 11, -10, -11, -13, 12, -3);

c = (-9, 1, 2, 5, -1, 5, 8, -2); f = (-4, -6, 3, -1, -6, -2, -1, -1);

κ₁ = 0.5; μ₁ = -5.0;

κ₂ = 0.0; μ₂ = 8.0;

Ответ:

x = (-5.991635, -1.983270, 2.202703, 2.144148, -0.380646, 0.754027, 0.750868, 2.607895, -4.130702, 8.0);

16)

a = (4, -1, -4, 5, -8, 2, -10, 7); b = (5, 6, 15, 9, -11, 6, -18, 10);

c = (-1, 3, -9, 1, -2, -2, -8, -1); f = (-8, 4, -10, -6, -5, -6, 5, -4);

κ₁ = 0.3; μ₁ = 6.0;

κ₂ = 0.2; μ₂ = -7.0;

Ответ:

x = (4.461884, -5.127054, 0.212263, -0.800211, -0.316914, 0.853279, -0.925381, 1.077137, -1.891833, -7.378366);

17)

a = (-2, 1, 9, -3, -2, 3, 2, -7); b = (11, -6, 14, 15, 10, -9, 5, -14);

c = (-6, 2, 4, 9, 7, -3, -2, -6); f = (9, 10, -8, -9, -7, -3, -1, 6);

κ₁ = 0.2; μ₁ = 3.0;

κ₂ = 0.5; μ₂ = 2.0;

Ответ:

x = (3.119164, 0.595821, -1.447383, 0.359941, 0.003183, -0.874714, 0.248682, -0.620759, -0.803217, 1.598392);

18)

a = (-5, 7, 10, -1, -5, -4, -10, -9); b = (15, 16, 18, 8, 17, 12, -20, -12);

c = (-10, 7, 6, -7, -10, -8, 7, 1); f = (-2, -8, 4, 5, -9, -3, -8, -1);

κ₁ = -0.7; μ₁ = -7.0;

κ₂ = -0.9; μ₂ = 4.0;

Ответ:

x = (-5.713466, -1.837905, 0.299875, 0.009619, 0.138019, -0.557924, -0.117480, 0.477741, 0.054289, 3.951140);

19)

a = (2, -5, -2, 8, -9, -9, 6, 2); b = (11, 16, -6, -14, 14, -21, 15, 10);

c = (-7, 9, 3, 4, 5, -10, 6, 5); f = (-8, 1, 9, 10, -6, 5, 10, -6);

κ₁ = 0.1; μ₁ = 1.0;

κ₂ = -0.1; μ₂ = 5.0;

Ответ:

x = (1.096402, 0.964015, 2.970996, -4.635095, -4.289526, -3.243152, 0.159679, 2.083512, -3.701792, 5.370179);

20)

a = (1, 8, -10, -8, 7, -2, -3, 9); b = (5, -16, 11, 17, 18, 4, -7, 18);

c = (-1, -5, -1, 9, -8, 1, 1, -6); f = (-6, -2, -6, -3, -9, -6, 5, -1);

κ₁ = -0.7; μ₁ = -9.0;

κ₂ = -0.5; μ₂ = -6.0;

Ответ:

x = (-9.574780, 0.821114, 0.530792, 0.015250, 0.859831, -1.943904, -2.496431, 0.097918, -1.803870, -5.098065);

21)

a = (-7, 4, -8, -1, -6, 2, 9, 6); b = (-12, -12, -18, 10, -12, 7, 21, 16);

c = (4, 6, 10, -8, -5, -5, 10, -8); f = (8, 5, 6, 10, 2, -5, 4, 4);

κ₁ = -0.9; μ₁ = -4.0;

κ₂ = -0.6; μ₂ = 4.0;

Ответ:

x = (-7.676075, 4.084528, 0.820453, -0.248780, 0.808558, -0.208205, -0.870578, -0.302091, 1.817911, 2.909253);

22)

a = (-5, 5, 4, 9, 8, -3, 10, 5); b = (7, 11, 10, 14, 11, -15, 17, 11);

c = (2, -4, -3, 2, 1, -10, 6, 6); f = (-3, -8, -7, 4, 9, -8, 8, -5);

κ₁ = -0.5; μ₁ = -6.0;

κ₂ = 0.2; μ₂ = -3.0;

Ответ:

x = (-4.195300, -3.609400, 0.644651, -0.738960, 0.729667, 0.217654, 0.768469, -0.418000, 1.236885, -2.752623);

23)

a = (-5, -4, -9, -7, 3, -5, 10, 9); b = (-13, 14, -17, 16, -8, 15, 20, 11);

c = (8, -9, 8, -7, -3, 10, 10, -2); f = (-6, 6, -1, -7, 2, 3, -10, 1);

κ₁ = 0.0; μ₁ = -8.0;

κ₂ = 0.7; μ₂ = 7.0;

Ответ:

x = (-8.0, 4.016768, 0.777248, -1.242844, -1.891640, -2.080904, 2.990770, -5.226607, 6.462444, 11.523711);

24)

a = (5, -8, -3, 9, 9, -6, 3, -5); b = (-16, -18, -6, -12, -17, 16, 11, 17);

c = (-8, -8, 2, -3, 8, 8, 6, -9); f = (1, -10, -1, -5, 6, 5, 10, 10);

κ₁ = -0.5; μ₁ = -6.0;

κ₂ = -0.8; μ₂ = 3.0;

Ответ:

x = (-4.697411, -2.605178, 2.149474, -0.981138, -0.219204, -0.399932, 0.146749, 0.031553, 1.535445, 1.771644);

25)

a = (-4, 10, 3, 8, 7, -5, -3, 10); b = (-9, -13, 8, 14, 18, 15, 13, 20);

c = (3, 1, 3, 4, 9, -7, -10, 7); f = (-7, -1, 6, 1, -8, 8, -5, -4);

κ₁ = 0.8; μ₁ = 7.0;

κ₂ = -0.2; μ₂ = -2.0;

Ответ:

x = (5.348944, -2.063820, -1.392867, 1.530925, -0.689601, -0.398249, 0.443964, 0.092958, 0.487657, -2.097531);

26)

a = (-7, -6, -2, -8, 5, -4, 7, 1); b = (-12, 13, 13, -10, -9, 15, 11, 10);

c = (5, -7, -10, 1, -3, 9, 1, 7); f = (-9, 1, -1, -3, -9, 10, -4, 5);

κ₁ = 0.6; μ₁ = -9.0;

κ₂ = 0.4; μ₂ = 6.0;

Ответ:

x = (-5.829481, 5.284198, 2.720802, 0.380749, 0.050813, 0.554118, 1.422333, -1.013169, -2.811471, 4.875412);

27)

a = (2, -2, -7, -6, 8, 9, -1, 3); b = (14, -12, -19, 12, 15, 12, -7, -8);

c = (9, 10, 9, -6, 6, 1, 5, 4); f = (-2, -7, 4, 2, 3, -9, -5, 2);

κ₁ = -0.5; μ₁ = -9.0;

κ₂ = 0.4; μ₂ = -8.0;

Ответ:

x = (-9.529833, 1.059665, 0.247150, -0.191487, 0.232422, 0.322998, -0.617392, -4.498279, -7.421068, -10.968428);

28)

a = (-8, -5, 4, -6, -5, -10, -4, 5); b = (15, 14, -14, -14, -14, 21, 9, -15);

c = (5, -8, -9, -5, 9, -8, 3, -8); f = (-9, -7, -10, 5, -8, -8, 2, 4);

κ₁ = -0.5; μ₁ = 7.0;

κ₂ = 0.2; μ₂ = -3.0;

Ответ:

x = (5.973073, 2.053853, 1.595358, 2.383218, -1.887068, 1.423930, 0.277743, 0.050839, 1.189506, -2.762099);

29)

a = (-6, 10, 2, -4, 1, 6, 6, 9); b = (11, 11, -8, -6, 8, -15, 18, -15);

c = (-3, -1, -3, 1, 6, 7, 10, 4); f = (-9, 10, 3, 6, 3, -5, 3, 9);

κ₁ = 0.7; μ₁ = -3.0;

κ₂ = -0.5; μ₂ = 2.0;

Ответ:

x = (-4.761800, -2.516858, 3.295123, 1.077777, -1.677323, 0.247169, 0.449996, 0.038132, 0.038636, 2.019318);

30)

a=(7, -5, -3, -1, 8, -1, 3, 3); b=(-10, -11, -9, 8, 15, 10, 14, 12);

c=(-1, -4, -5, -5, 6, -9, -9, 9); f=(6, -7, 8, 3, -4, -7, 1, -1);

κ₁ = 0.0; μ₁ = -5.0;

κ₂ = -0.7; μ₂ = -8.0;

Ответ:

x=(-5.0, -4.420842, 3.208422, -1.547107, -0.740260, -1.474994, 4.007833, 5.394814, 9.616765, -14.731735).

Дата добавления: 2014-01-03