В зоне обслуживания

Решения по развитию складской сети необходимо прини­мать на основе анализа полной стоимости, что означает учет всех экономических изменений, возникающих при изменении количества складов в логистической системе.

Рассмотрим модель системы распределения материального потока, представленную на рис.82. Допустим, что предприятие поставщик, обслуживает сеть оптовых покупателей, расположенных на определенной территории. Количество покупателей и объемы потребляемых ими потоков в рамках данной задачи являются величинами постоянными.

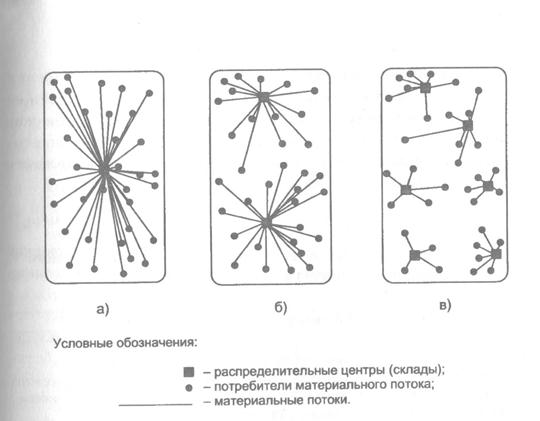
Рис. 82. Варианты организации распределения материального потока: а — с одним распределительным центром; б — с двумя распределительными центрами; в — с шестью распределительными центрами

На рисунке представлены три варианта организации распре деления: с помощью одного, двух и шести складов (соответствен но рисунки а, б и в). Очевидно, что в случае принятия варианта (а) транспортные расходы по доставке будут наибольшими. Вариант (в) предполагает наличие шести распределительных центров, максимально приближенных к местам сосредоточения потре расходы по товароснабжению будут минимальными. Однако появление в системе распределения пяти дополнительных складов увеличивает эксплуатационные расходы, затраты на доставку товаров на склады, затраты на управление всей распределитель­ной системой. Не исключено, что дополнительные затраты в этом случае могут значительно превысить экономический выигрыш, полученный от сокращения пробега транспорта, доставляюще­го товары потребителям.

В табл. 24 приведены условные зависимости отдельных видов издержек, связанных с функционированием системы распределения, от количества входящих в эту систему складов. Как видим, при изменении количества складов в системе распределения часть издержек, связанных с процессом доведения материального потока до потребителя, возрастает, а часть — снижается. В нашем условном примере предпочтительнее ока­зался вариант, согласно которому район должен обслуживать­ся двумя складами. В этом случае суммарные затраты являют­ся минимальными (1735 тыс. руб. / мес.).

Таблица 24

Условный пример решения задачи определения оптимального количества складов в логистической системе

Кол. складов, ед.	Издержки системы распределения, тыс. руб./мес.
по дос­тавке товаров на скла­ды	по дос­тавке товаров со скла­дов	связан­ные с хранени­ем запа­сов	связан­ные с эксплуа­тацией складов	потери от снижения продаж, связанные с удалением снаб­жающего склада от потребителя	всего

Как видим, при изменении количества складов в системе распределения часть издержек, связанных с процессом до­ведения материального потока до потребителя, возрастает, а часть снижается. Это позволяет ставить и решать задачу поиска оптимального количества складов. Рассмотрим графический метод решения данной задачи.

Выберем в качестве независимой переменной величину N — количество складов, через которые осуществляется снаб­жение потребителей. В качестве зависимых переменных будем рассматривать следующие виды издержек:

• транспортные расходы;

• расходы на содержание запасов;

• расходы, связанные с эксплуатацией складского хозяй­ства;

• расходы, связанные с управлением складской системой;

• потери продаж, вызванные удалением снабжающего скла­да от потребителя.

Для определения оптимального количества складов необ­ходимо в разрезе всей системы распределения оценить, как в зависимости от изменения N изменяются те или иные расхо­ды и потери.

Охарактеризуем зависимость издержек каждого вида от количества складов. 1. Зависимость величины затрат на транспортировку от количества складов в системе распределения (функция f ₁, рис. 83).

В рамках решения данной задачи будем исходить из предположения, что для каждого значения переменной (количество складов) расположение складов на обслуживаемой территории оптимально.

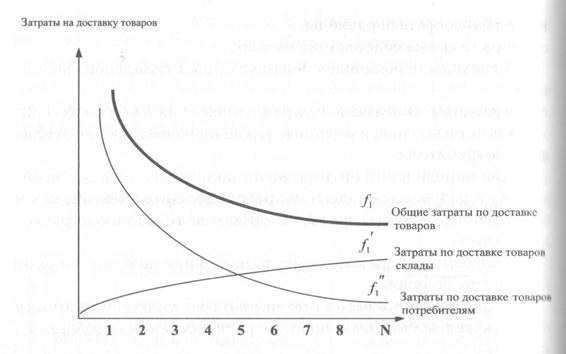
Рис.83. Зависимость затрат на транспортировку от количества складов

Дата добавления: 2014-01-03