Определение места расположения склада на обслуживаемой территории

В предыдущем параграфе, решая задачу определения опти­мального количества складов в системе распределения, в качестве одной из главных зависимых переменных рассматривались транспортные расходы по доставке товаров потребителям мате­риального потока со складов распределительной системы. Из ­ менение этой величины изучалось в зависимости от изменений количества складов в системе распределения. Однако величина транспортных расходов может существенно меняться не только в зависимости от количества складов, но также и в зависимости от места расположения этих складов на обслуживаемой терри­тории (в предыдущем параграфе исходили из предположения, что склады на территории расположены оптимально).

Задача размещения распределительного центра приобре­тает актуальность при наличии развитой транспортной сети, так как в противном случае решение, скорее всего, будет оче­видным. Например, если на территории района есть только две пересекающиеся магистрали, вдоль которых расположены все потребители, то очевидно, распределительный центр целесоо­бразно разместить на пересечении магистралей.

Задача размещения распределительных центров может формулироваться как поиск оптимального решения или же как поиск субоптимального (близкого к оптимальному) решения. На­укой и практикой выработаны разнообразные методы решения задач обоих видов. Кратко охарактеризуем некоторые из них.

Метод полного перебора. Задача выбора оптимального ме­ста расположения решается полным перебором и оценкой всех возможных вариантов размещения распределительных цен­тров и выполняется на компьютерах методами математиче­ского программирования. Однако на практике в условиях раз­ветвленных транспортных сетей метод может быть неприме­ним, так как число возможных вариантов по мере увеличения масштабов сети, а с ними и трудоемкость решения растут по экспоненте^[63].

Эвристические методы. Гораздо менее трудоемки субопти­мальные, или так называемые эвристические методы определе­ния места размещения распределительных центров. Эти методы эффективны для решения больших практических задач; они дают хорошие, близкие к оптимальным результаты при невы­сокой сложности вычислений, однако не обеспечивают отыска­ния оптимального решения. Название "эвристические" означа­ет, что в основе методов лежит человеческий опыт и интуиция (в отличие от формальной процедуры, лежащей в основе мето­да полного перебора). Метод основан на предварительном отка­зе от большого количества очевидно неприемлемых вариантов. Опытный специалист-эксперт анализирует транспортную сеть района и непригодные, на его взгляд, варианты исключает из расчетов. Таким образом, проблема сокращается до управляе­мых размеров с точки зрения количества альтернатив, которые необходимо оценить. Остаются лишь спорные варианты, по ко­торым у эксперта нет однозначного мнения. Для этих вариантов расчеты выполняются по полной программе.

Метод определения центра тяжести физической модели системы распределения (используется для определения места расположения одного распределительного центра). Метод аналогичен определению центра тяжести физического тела. Суть его состоит в следующем. Из легкого листового материала вырезают пластину, контуры которой повторяют границы района обслу­живания. На эту пластину в местах расположения потребителей материального потока укрепляют грузы, вес которых пропорцио­нален величине потребляемого в данном пункте потока. Затем модель уравновешивают (рис. 86). Если распределительный центр разместить в точке района, которая соответствует точке центра тяжести изготовленной модели, то транспортные расходы по распределению материального потока на территории райо­на будут минимальны.

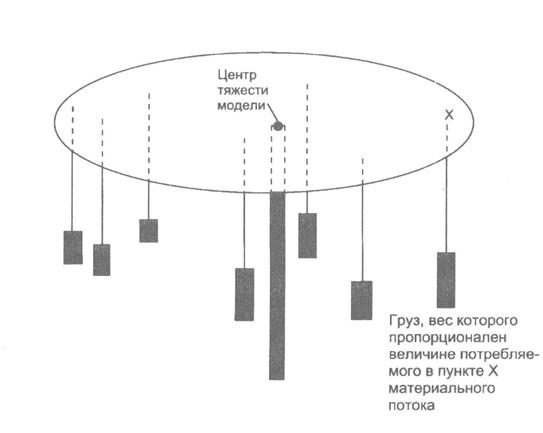
Рис. 86. Определение места расположения склада методом построения физической модели материальных потоков

При использовании метода надо учесть неизбежную ошиб­ку, которая будет внесена весом пластины, выбранной для неновы модели. Эта ошибка выразится присутствием на модели мнимого потребителя, расположенного в центре тяжести самой пластины и с грузооборотом, пропорциональным ее весу. Ошибка будет тем меньше, чем меньше вес пластины.

Применение описанного метода имеет одно ограничение. На модели расстояние от пункта потребления материального по­тока до места размещения распределительного центра учиты­вается по прямой. В связи с этим моделируемый район должен иметь развитую сеть дорог, так как в противном случае будет нарушен основной принцип моделирования — принцип подобия модели и моделируемого объекта.

Методом определения центра тяжести можно оптимизировать, например, размещение склада предприятия оптовой тор­говли, снабжающего магазины района продовольственными то­варами. Уравновесить в этом случае необходимо грузооборо­ты обслуживаемых магазинов. Если зона обслуживания опто­вого склада включает несколько населенных пунктов, снабжа­емых определенной группой товаров только с этого склада, то на модели распределительной системы грузы могут быть пропорциональны численности населения соответствующих насе­ленных пунктов.

Задача определения точки территории, соответствующей центру тяжести физической модели системы распределения, может быть решена с помощью известных математических фор­мул. В качестве примера найдем место для размещения склада в распределительной системе, обслуживающей пять потребителей (рис.87). Нанесем на карту района обслуживания координатные оси и найдем координаты точек, в которых размещены потребите­ли материального потока, например магазины (на рис. 87 указаны номера магазинов, в скобках — их месячный грузооборот).

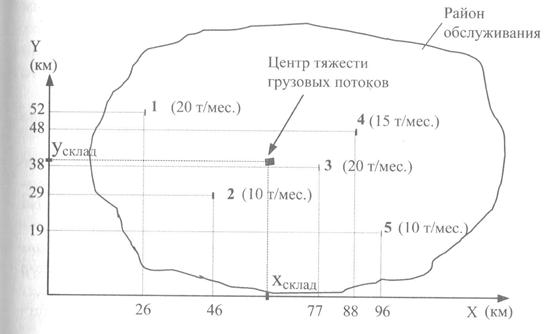
Рис. 87. Определение места расположения склада методом поиска центра тяжести физической модели системы распределения

Координаты центра тяжести грузовых потоков (х_склад, у_склад), т. е. точки, в которой может быть размещен распределительный склад, определятся по формулам

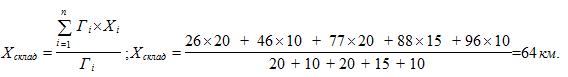
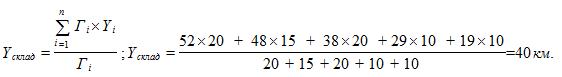
где Г _i — грузооборот i -го потребителя;

Х_i, Y_i — координаты i -го потребителя,

n — количество потребителей.

Точка территории, обеспечивающая минимум транспортной работы по доставке, в общем случае не совпадает с найденным центром тяжести, но, как правило, находится где-то недалеко Подобрать приемлемое место для склада позволит последующий анализ возможных мест размещения в окрестностях найденного центра тяжести.

Определение места расположения распределительного центра методом пробной точки^[64].

Предлагаемый метод позволяет определить оптимальное место размещения распределительного склада в случае прямоугольной конфигурации сети автомобильных дорог на обслуживаемом участке.

Вначале на примере отдельного линейного участка транс портной сети разберем суть метода. Пусть на участке дороги произвольной длины (участок АB, рис. 88), имеется 8 потре­бителей материального потока: А, В, С, D, Е, F, G и Н. Месячный объем завоза товаров к каждому из них указан в скобках. Оптимальное место расположения распределительного склада легко определить методом, который можно назвать как "метод пробной точки".

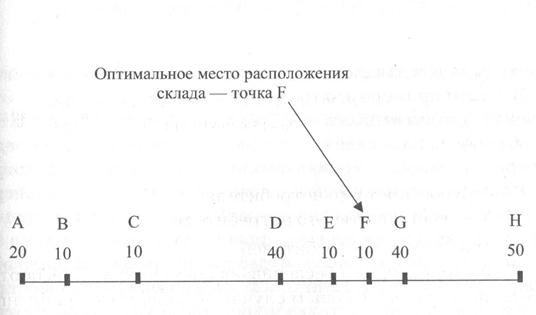
Рис.88 Определение оптимального места расположения склада на участке обслуживания методом пробной точки (числами указан грузооборот потребителей, тонн в месяц)

Суть метода состоит в последовательной проверке каждого отрезка обслуживаемого участка.

Введем понятие пробной точки отрезка, а также понятия левого и правого по отношению к этой точке объема завоза товаров.

Пробной точкой отрезка назовем любую точку, находящую­ся на этом отрезке и не принадлежащую его концам (т. е. пробная точка не совпадает с точками А, В, С, D, Е, F, G и Н).

Левый от пробной точки точке объем завоза това­ров — товаропоток к потребителям, расположенным на всем участке обслуживания слева от этой точки.

Правый от пробной точки точке объем завоза товаров — товаропоток к потребителям, расположенным справа от нее.

Участок обслуживания проверяют, начиная с крайнего лево­гоконца участка. Вначале анализируют первый отрезок участ ­ ка (в нашем случае, отрезок АВ). На данном отрезке ставится пробная точка и подсчитывается сумма объемов завоза товаров к потребителям, находящимся слева и справа от поставленной точки. Если объем завоза к потребителям, находящимся спра­ва больше, то проверяется следующий отрезок. Если меньше, то принимается решение о размещении склада в начале анали­зируемого отрезка.

Перенос пробных точек продолжается до тех пор, пока не появится точка, для которой сумма объемов завоза к потреби­телям с правой стороны. Решение принимается о размещении склада в начале этого отрезка, т. е. слева от пробной точ­ки. В нашем примере это точка F.

Рассмотрим вариант, представленный на рис. 89, когда сум­ма объемов завоза слева и справа от пробной точки очередного отрезка становится одинаковой. Отметим начало этого отрез­ка — точку О как первое из возможных мест расположения рас­пределительного склада на участке обслуживания и продолжим анализ до появления отрезка, для пробной точки которого зна­чение левого объема завоза будет выше правого. Начало этот отрезка (точка Р) определит последнее из возможных мест рас положения распределительного центра на участке обслужива­ния. Распределительный центр может быть расположен в лю­бой из точек отрезка ОР участка обслуживания.

Дата добавления: 2014-01-03