Обучение решению типовых задач

План

1. Основаниядля классификации текстовых задач по типам

2. Этапы обучения решению задач определенного типа

3. Содержание подготовительной работы к решению типовых задач

4. Особенности технологии ознакомления со способом решения задач нового типа

5. Методические приемы формирования умения решать задачи определенного типа

6. Типовые задачи с пропорциональными величинами

Литература дополнительная:

Бантова М.А. и др. Методика преподавания математики в начальных классах. – М.,1984.

Истомина Н.Б. Методика обучения математике в начальных классах. – М.,1999,гл.4.

Кулебякина Л.Я. Работа над простой задачей на этапе поиска ее решения//Начальная школа. – 2002. - №10.

Матвеева Н.А. Использование схематического чертежа в моделировании простых текстовых задач//Начальная школа. – 2002. - №10

Медведская В.Н.,Гудалина Г.И. 1500 задач и примеров с объяснениями решений. – Мн.,2005.

1.Основания для классификации текстовых задач по типам

Распределение задач по классам (типам) на основании какого-либо общего признака имеет определенное значение для методической подготовки учителя:

1) знание специфических особенностей задач одного и того же типа и знание соответствующей ему методики являются методологическими, т.е. фундаментальными, общими, порождающими многообразие частных знаний как варианта общего знания;

2) дает экономию временных затрат на профессиональную подготовку учителя;

3) обеспечивает системность знаний (а не их хаотичность и разрозненность), оперативность и гибкость применения этих знаний в конкретных условиях.

Итак, цель изучения классификации задач – систематизация знаний об эффективных методах обучения решению задач.

Нужно ли знать классификацию арифметических задач учителю? А ученику?

В методической науке традиционными являются следующие основания классификации задач:

1) количество действий для ответа на вопрос задачи (простые и составные: в 2-3-4 действия);

2) сюжет задачи (на движение, на совместную работу, на переливание и др.);

3) взаимосвязь между данными и искомыми задачи, т.е. математическая структура задачи

например,

а) задачи на нахождение суммы, остатка, на увеличение числа в несколько раз и другие типы простых задач;

б) для составных – задачи на нахождение неизвестного по сумме и кратному отношению, по сумме и разности, по двум разностям и др.;

4) способ решения (на простое тройное правило, на пропорциональное деление, на предположение, на разностное сравнение и др.)

Какие из перечисленных признаков являются внешними, несущественными?

Как видим, единого основания для классификации многообразия текстовых задач нет. Если бы это было возможно, то для решения любой арифметической задачи достаточно было бы знать классификацию, а значит и способы решения задач каждого отдельного типа:

			Применяю общий способ для решения данной задачи

Подобная попытка предпринята в учебных пособиях В.Д. Герасимова. В качестве внешних признаков различения задач по типам он использует графические схемы задач и их краткие записи. В частности, группы пропорционально зависимых величин (скорость, время, расстояние; урожайность, площадь, урожай; масса одного ящика, количество ящиков, общая масса и др.) обобщаются символами К₁, К₂, ОК, где, например, К₁ – стоимость одного предмета (ил цена); К₂ – количество таких предметов; ОК – стоимость всех этих предметов.

Основная задача такого обучения – учить находить (прежде всего в памяти) соответствующую конкретной задаче «вывеску» (шаблон, штамп, т.е. название типа или другие заменяющие его модели – чертеж, схема, краткая запись) и взять под этой вывеской то, что нам нужно, в нашем случае – способ решения конкретной задачи.

Сопоставьте эту ситуацию с покупкой продуктов в гастрономе: хлеб берем в одном отделе, молоко – в другом и т.д.

На все случаи реальной жизни, которые могут стать прообразами текстовых задач, шаблонов нет и быть не может. Следовательно, обучение решению задач нельзя сводить только к обучению решению типовых задач. Результатом такого обучения станут формализм знаний и их закостенелость, беспомощность ребенка в нестандартной ситуации и другие негативные последствия.

Нужно ли вообще обучать решению типовых задач?

Вспомним сформулированную нами цель обучения решению задач:

сформировать научить решать задачи

общие умения определенных стандартами

и общий подход образования типов

Логически возможными представляются три модели обучения.

А.

			Применение общих знаний для любых задач (в т.ч. и нетиповых)

Такой подход был реализован в учебниках до 90-х годов прошлого столетия. Например, в учебниках М.И.Моро.

Отказ от классификации задач, т.е. параллельное решение неоднотипных задач

Общее знания и умения

Применение общих знаний и умений для любых задач

Б.

Этого подхода придерживаются авторы белорусских учебников – Т.М.Чеботаревская, В.Л.Дрозд и др.

В. Рационально сочетание моделей

А и Б, когда обучение решению типовых задач органично включается в систему работы по формированию общих умений и общего подхода к решению арифметических задач.

Какую из моделей А, Б, В выбрали бы вы?

2.Этапы обучения решению задач определенного типа

В работе над задачами каждого типа выделяется последовательность этапов:

I.Подготовительная работа

II.Ознакомление со способом решения

III.Формирование умения решать задачи данного типа

Проанализируйте с этой точки зрения ОС №8-11. Будет ли аналогично организовано обучение решению типовых составных задач? Например, задач на движение?

3.Содержание подготовительной работы к решению типовых задач

Решение задач одного типа основано на одних и тех же связях между данными и искомым. Такие задачи отличаются друг от друга только сюжетным содержанием и числовыми данными. Поэтому цель подготовительной работы – обеспечить условия для осознанного перевода на математический язык вполне определенных для данного типа задач связей между данными и искомыми.

Главная учебная задача этого этапа – понимание смысла математических понятий, отношений, закономерностей.

В разных типах задач описываются различные связи между искомым и данными, следовательно, содержание работы на подготовительном этапе принципиально зависит от типа задачи и существенно различается для задач разных типов.

Сравните содержание подготовительной работы в ОС №8-11.

Но при этом для каждого нового типа задач применяются одни и те же, общие для всех типовых задач, технологические приемы:

1) связь с жизненным опытом детей;

2) широкое использование методов демонстрации и практической работы учащихся для подлинного понимания смысла арифметических действий, отношений сравнения, конкретного смысла величин и т.п.

Например, в схемах №8,9,10; в задачах на движение – практическая деятельность с моделями скоростей в виде прямоугольников разного цвета.

3) обобщение частных наблюдений разнообразных конкретных фактов или явлений и их описание на математическом языке.

Например, стало меньше, значит, надо вычитать; «увеличить в раз» - надо умножать; «чтобы найти скорость, надо расстояние поделить на время».

4) отработка вычислительных умений и навыков.

Подготовительную работу можно считать завершенной, если учащиеся вполне осознанно и уверенно описывают соответствующие данному типу задач реальные ситуации на языке математики.

Таким образом, подготовительная работа включает:

4. Особенности технологии ознакомления со способом решения задач нового типа

Для любых типов задач работа на этапе ознакомления строится по одной и той же схеме:

			применение способа в аналогичных условиях

На этом этапе должны соблюдаться следующие требования:

1. Тщательный подбор текстовой задачи для ознакомления со способом решения.

В первой задаче не должно быть ничего отвлекающего внимание детей от поставленной цели – «открыть», следовательно, в ее тексте используются знакомый, соответствующий жизненному опыту детей сюжет и удобные для вычислений данные в условии.

2. Выполненное решение (тем более впервые!) должно быть проанализировано и осмысленно:

- Как решали?

- Почему сначала узнали …, а потом …?

- Что помогло решить задачу? и т.п.

Это и есть «взгляд назад»

3. На этом же уроке проводится первичное закрепление нового способа решения – решаются еще 1-2 аналогичные задачи с полным объяснением.

4. Ограниченное применение творческой работы и даже некоторых способов проверки, если они не способствуют напрямую достижению поставленной на данный урок главной цели – «открыть» способ решения задач нового типа.

В схемах №8-11 найдите запись: «Осуществляется переход от практического способа решения к арифметическому.

5.Методические приемы формирования умения решать задачи определенного типа

На этапе формирования умения ставится цель: научить решать любую задачу данного типа, т.е. обобщить способ их решения.

Приемы, помогающие детям придти к обобщению:

1. Решение достаточного количества задач данного типа.

2. Включение задач данного типа в содержание уроков в перемежении с другими как типовыми, так и нетиповыми задачами.

3. Сравнение задач этого типа со сходными им в некоторых отношениях другими задачами.

4. Выполнение упражнений творческого характера

5. Решение задач с буквенными данными.

В схемах №8-11 прочитайте то, что относится к третьему этапу обучения решению типовых задач. Объясните, почему для разных типов задач требуется одно и то же.

6. Типовые задачи с пропорциональными величинами

Продолжите список пропорционально зависимых величин.

	К1 Цена Скорость Длина Урожайность		К Количество Время Ширина Площадь		ОК Стоимость Расстояние Площадь Урожай

Для каждой группы взаимосвязанных величин конкретизируйте общие формулы:

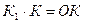
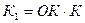
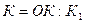
Сформулируйте условия, при которых эти величины будут находиться в прямопорциональной зависимости, в обратнопропорциональной зависимости.

Задачи с пропорциональными величинами являются основным средством ознакомления учащихся с прямой и обратной пропорциональной зависимостью величин. В процессе их решения идет усвоение этих зависимостей. Поэтому в методике вопрос обучения младших школьников решению этих задач, рассматривается как специальный.

Задачи с пропорциональными величинами могут быть простыми и составными.

Например:

Ц К Ст. Ц К Ст.

200 3? I 200 3

одинаковая

? 3 600 II 300?

200? 600

Простые задачи с пропорционально зависимыми величинами являются тем учебным материалом, на котором организуется открытие и обобщение существующих между величинами связей: 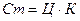, ,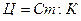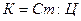и т.п.

Поэтому такие задачи являются обязательным компонентом содержания подготовительной работы к решению состовных задач.

Из состовных задач с пропорциональными величинами в начальных классах рассматриваются следующие типы:

· Задачи на нахождения четрертого пропорционального (на простое тройное правило)

· Задачи на пропорциональное деление

· Задачи на нахождение неизвестного по двум разностям

· Задачи на движение

· Задачи на совместную работу

В начальной школе работа над задачами на движение и на совмастную работу имеет пропедевтический характер и будет продолжаться в средних классах.

Рассмотрим подробнее лишь три из названых пяти типов задач:

1) на нахождение четвертого пропорционального

Скорость Время Расстояние

I 3ч 12км

одинаковая

II 5ч? км

Почему дано такое название типа?

2) на пропорциональное деление

Скорость Время Расстояние

I 3ч? км

одинаковая 32 км

II 5ч? км

Почему дано такое название типа?

3) на нахождение неизвестного по двум разностям

Скорость Время Расстояние

I 3ч?км

одинаковая

II 5ч? км на 8 км больше

Почему дано такое название типа?

Составьте аналогичные задачи с величинами цена, количество, стоимость; масса одного пакета, количество пакетов, общая масса. Требование «одинаковая» предъявляйте не только к величине К₁. Назовите общие признаки задач данных типов.

Как из задачи на нахождение четвертого пропорционального можно получить задачи новых типов – на пропорциональное деление и на нахождение неизвестного по двум разностям?

Общие признаки составных типовых задач с пропорциональными величинами:

1) говорится о трех взаимозависимых величинах;

2) одна из них по условию задачи принимает постоянное значение;

3) две другие величины являются переменными, связанными между собой так, что изменение одной из них влечет за собой соответсвующее изменение другой величины.

Эти признаки сходства наилучшим образом выявляются в краткой записи данных типов задач в форме прямоугольной таблицы. Употребляемые для обозначения ее столбцов термины, т.е. названия величин, облегчают поиск этих задач. Проводимые при этом рассуждения способствуют закреплению знаний о взаимосвязи рассматриваемых величин.

На этапах осмысления содержания задач с пропорциональными величинами и поиска плана их решения весьма полезным может оказаться и графическое моделирование.

Выполните построения отрезков, соотвествующих текстам приведенных выше примеров кратких записей задач.

Выполните для этих задач прикидку ответа. Назавите типы задач с пропорциональными величинами, для которых прикидка ответа позволяет выявить пропорциональную зависимость между переменными величинами.

Поиск плана решения любой задачи можно проводить методами анализа, синтеза, а также аналитико-синтетаческим методом.

К “открытию” учащимися способов решения задач на пропорциональное деление и на нахождение неизвестного по двум разностям подводят и наводящие вопросы. В рассматриваемых нами задачах это вопросы:

- Что обозначает число 32 км? (расстояние, которое туристы прошли за два дня, т.е. за 3 ч да еще за 5ч.) Значит, что можно узнать сначала? Зачем нам нужно знать, за сколько часов туристы прошли 32 км? (Чтобы найти скорость).

- Почему во второй день туристы прошли на 8 км больше, чем в первый день? (Были в пути не 3 ч, а 5ч) за сколько часов они прошли “лишние” 8 км? (За 2 часа). Значит, что надо узнать сначала?

Реализация намеченого плана решения, т.е. запись решения этих задач выполняется по действиям с пояснениями или с вопросами, а для задач на нахождение в виде числового выражения, что позволяет направить внимание учащихся на зависимость между величинами и на способ решения (без отвлечения на промежуточные вычисления).

Для задач с пропорциональными величинами применимы всевозможные способы проверки и формы творческой работы. Следует, однако, обязательно обратить внимание учащихся на возможность решения этих задач не одним, а двумя способами.

Для задач на нахождение четвертого пропорционального – это способ отношений, когда его допускает подбор числовых данных. Если в рассматриваемом нами примере задачи вместо 5ч было бы 6ч, то сначала можно узнать, во сколько раз больше времени туристы были в пути во второй день, чем в первый. А значит, и расстояние, которое они пройдут с той же скоростью, во второй день будет во столько же раз больше,чем в первый день.

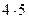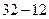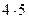В задачах на пропорциональное деление и на нахождение неизвестного по двум разностям заключительный шаг решения можно выполнить двумя способами: или ; или .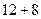

Из многообразия форм творческой работы над решенной задачей для задач с пропорционально зависимыми величинами наиболее продуктивными являются:

1) составление задач, аналогичных решенной, с теми же величинами;

2) составление задач, аналогичных решенной, но с другой группой величин;

3) составление задач по решению, по краткой записи, обратных;

4) преобразование решенной задачи в задачу другого типа;

5) решение задачи другим способом.

Дата добавления: 2014-01-03