Решение матричных игр в чистых стратегиях

Целью участников любой матричной игры является выбор наиболее выгодных стратегий, доставляющих игроку А макси­мальный выигрыш, а игроку В минимальный проигрыш. Стра­тегию игрока А называют оптимальной, если при ее примене­нии выигрыш игрока А не уменьшается, какими бы стратеги­ями не пользовался игрок В. Оптимальной для игрока В на­зывают стратегию, при использовании которой проигрыш иг­рока В не увеличивается, какие бы стратегии не применял игрок А.

Предположим, что игроку А надлежит сделать свой выбор. Анализируя платежную матрицу (см. таблицу 7.1), он для каж­дой чистой стратегии A_i (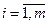) сначала найдет минималь­ное значение α_i ожидаемого выигрыша: 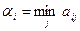(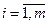), а затем из всех α_i выделит наибольшее 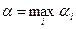и выберет соответствующую ему чистую стратегию 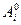. Это и будет наи­более предпочтительная (гарантирующая) в данных условиях стратегия игрока А. Ее называют максиминной, поскольку она отвечает величине

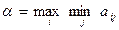(7.1)

Число α, определяемое по формуле (7.1), называется ниж­ней чистой ценой игры (максимином). Оно показывает, какой минимальный выигрыш может получить игрок А, правильно применяя свои чистые стратегии при любых действиях игро­ка В.

В свою очередь, игрок В, стремясь минимизировать проиг­рыш, при выборе наиболее предпочтительной стратегии исполь­зует принцип осторожности так: сначала он для каждой чистой стратегии В_j (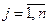) найдет максимально возможный про­игрыш 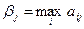(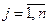), а затем среди β_j вы­берет минимальное значение 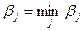, которому и будет со­ответствовать искомая чистая стратегия 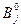. Ее называют ми­нимаксной, так как она соответствует величине

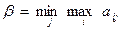(7.2)

Число β, определяемое по формуле (7.2), называется верх­ней чистой ценой игры (минимаксом). Оно показывает, какой максимальный проигрыш может быть у игрока В при пра­вильном выборе им своих чистых стратегий независимо от действий игрока А.

Если в матричной игре нижняя и верхняя чистые цены совпадают, т.е. α = β, то эта игра имеет седловую точку в чистых стратегиях и чистую цену игры ν = α = β. Оптимальными для игроков будут соот­ветственно максиминная и минимаксная стратегии, а чистой ценой игры – седловой элемент платежной матрицы. Если игра седловой точки не имеет, то решение игры затрудняется

Таким образом, правильно используя чистые стратегии, игрок А обеспечит себе выигрыш не меньше α, а игрок В в результате правильного применения своих чистых стратегий не позволит игроку А выиграть больше, чем β.

Дата добавления: 2014-01-03