Решение статистических игр по различным критериям

Статистические игры (игры с природой) – это парные матричные игры, в которых сознатель­ный игрок А (статистик), заинтересованный в наиболее выгод­ном для него исходе игры, выступает против участника, совер­шенно безразличного к результату игры (природой П).

Статистик может использовать несколько стратегий A₁,..., А_m. Природа также обладает множеством стратегий (состоя­ний) П₁,..., П_n. Под состоянием природы понимается полная совокупность внешних условий, в которых статистику приходится выбирать свою стратегию.

В своих взаимоотношениях с природой статистик может пользоваться как чистыми стратегиями A_i, так и смешанными стратегиями 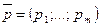. Если он имеет возможность оценить последствия применения каждой своей чистой стратегии А_i в зависимости от любого состояния П_j природы, т. е. если ему известен численный результат a_ij для каждой допустимой комбинации (A_i; П_j), то статистическую игру можно задать платежной матрицей [ а_ij ] (таблица 7.3).

Таблица 7.3 - Платежная матрица игры

Аi	Пj	рi
П1	…	Пn
А1	а11	…	a1п	р1
…	…	…	…	…
Am	am1	…	amn	рm
βj	β1	…	βn

Часто построение платежной матрицы является трудоемким этапом подготовки принятия решения. Поэтому при анализе игры с природой вводится показа­тель, позволяющий оценить, насколько то или иное состоя­ние природы влияет на исход ситуации. Этот показатель на­зывается риском.

Риском r_ij статистика, когда он пользуется чистой стра­тегией А_i при состоянии П_j природы, называется разность между максимальным выигрышем 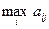, который он мог бы получить, достоверно зная, что природой будет реализо­вано именно состояние П_j, и тем выигрышем a_ij, который он получит, используя стратегию А_i, не зная, какое из состоя­ний П_j природа действительно реализует. То есть элементы матрицы рисков определяются по формуле

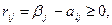(7.7)

где β_j – максимально возможный выигрыш статистика при состоянии П_j (макси­мальный элемент j -го столбца платежной матрицы (таблица 7.4)), т. е. .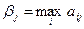

Таблица 7.4 - Платежная матрица игры

Аi	Пj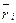
П1	…	Пn
А1	r11	…	r1п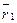
…	…	…	…	…
Am	rm1	…	rmn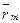
qj	q1	…	qn

Решение статистической игры может находиться либо в смешанных стратегиях, либо в чистых стратегиях.

Учитывая специфику статистических игр, при поиске оп­тимальных решений обращаются к различным критериям, дающим некоторую логическую схему принятия решения. Поскольку критерии формулируются на основе здравого смысла, интуиции и практической целесообразности, то они помогают оценить принимаемое решение с различных пози­ций, что позволяет избежать грубых ошибок в хозяйствен­ной деятельности.

Применяется две группы критериев, использующих и не использующих априорные вероятности q_j состояний при­роды. К первой группе относятся критерии Байеса и Лапла­са.

В качестве оптимальной по критерию Байеса принимает­ся чистая стратегия А_i, при которой максимизируется сред­ний выигрыш статистика

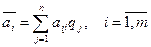, (7.8)

то есть обеспечивается 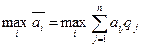. (7.9)

Если статистику представляются в равной мере правдо­подобными все состояния П_j природы, то 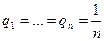, и оптимальной по критерию Лапласа считается чистая стра­тегия А_i, обеспечивающая

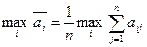. (7.10)

Ко второй группе критериев, применяемых при неизвест­ных априорных вероятностях состояний природы, относятся критерии Вальда, Сэвиджа и Гурвица.

Критерий Вальда – это максиминный критерий, который является критерием крайнего песси­мизма, так как здесь статистик исходит из предположения, что природа «действует» против него наихудшим образом, т. е. реализует такие состояния П_j, при которых величина его вы­игрыша принимает наименьшее значение. Оптимальной по кри­терию Вальда считается чистая стратегия А_i, при которой наименьший выигрыш статистика будет максимальным, то есть ему обеспечивается максимин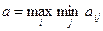

Для смешанных стратегий критерий Вальда формулиру­ется так: оптимальной считается та смешанная стратегия, при которой минимальный средний выигрыш статистика 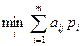будет максимальным, то есть стратегия р*, найденная из условия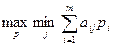

Критерий Сэвиджа, как и критерий Вальда, является кри­терием крайнего пессимизма. Оптимальной по критерию Сэвиджа считается та чистая стратегия А_i, при которой минимизируется величина r_i мак­симального риска, то есть обеспечивается .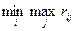

Для смешанных стратегий критерий Сэвиджа формули­руется так: оптимальной считается та смешанная стратегия, при которой максимальный средний риск статистика 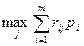минимизируется, то есть стратегия р*, найденная из условия .

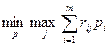Критерий Гурвица, называемый критерием пессимизма-оптимизма, рекомендует рассчитывать на нечто среднее. Оптимальной по критерию Гурвица считается чистая стратегия А_i, найденная из условия 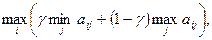где 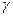принадлежит интервалу (0; 1) и выбирается из субъективных сооб­ражений.

При 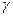= 1 критерий Гурвица превращается в критерий крайнего пессимизма Вальда, а при 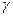= 0 — в критерий край­него оптимизма.

Надо отметить, что анализ практических ситуаций следу­ет проводить по нескольким критериям, что позволит глубже вникнуть в суть явления и выбрать обоснованное решение.

Дата добавления: 2014-01-03