Дифференцирование функций

Производной функции 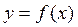в точке х называется конечный предел отношения приращения функции 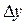к приращению аргумента :

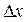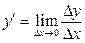, (16)

где .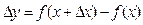

Другие обозначения производной: .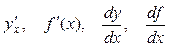

Если существует производная функции 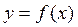в точке х, то функция называется дифференцируемой в этой точке. Дифференцирование функции – это процесс нахождения производной 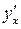. При дифференцировании используют таблицу производных и правила дифференцирования.

Таблица производных основных элементарных функций.

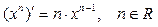
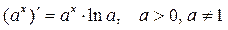
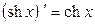
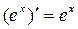
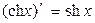
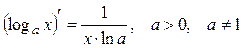
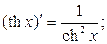
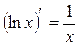
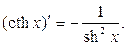
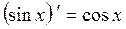
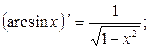
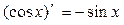
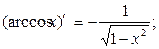
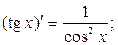
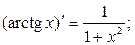
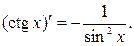
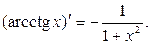
Основные правила дифференцирования.

1) Производная от постоянной равна нулю:

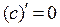. (17)

2) Производная алгебраической суммы (u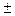v) двух дифференцируемых функци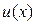й и 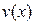существует и равна алгебраической сумме производных этих функций:

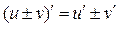(18)

3) Производная произведения двух дифференцируемых функци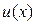й и 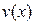существует и вычисляется по формуле:

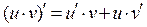. (19)

4) Производная отношения двух дифференцируемых функци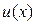й и 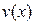существует и вычисляется по формуле:

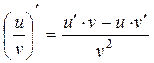. (20)

5) Постоянный множитель можно выносить за знак производной:

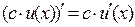(21)

6) Производная от сложной функции: если 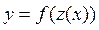, где f (z) и z (x) –дифференцируемые функции, то 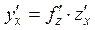(«правило цепочки»).

7) Производная от функции,заданной неявно: если функция 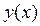задана уравнением 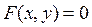, то для нахождения 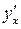нужно продифференцировать обе части тождества 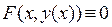по аргументу х и из полученного равенства найти 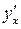как решение линейного уравнения.

8) Производная от функций 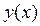, заданной параметрически: если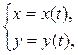где x (t), y (t) – дифференцируемые функции, то:

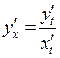. (22)

Производные высших порядков:производная 2-го порядка: ,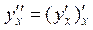

3-го порядка: 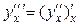и т.д. Для обозначений производных высшего порядка используются также символы вида: 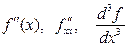. Производные 4 и более высоких порядков обозначаются при помощи римских цифр: 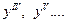. Производная n -го порядка обозначается 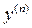, она получается n -кратным дифференцированием функции : .

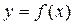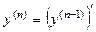Дата добавления: 2014-01-03