
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Ускорение точки
|
|
|
|
Пусть теперь известна функция 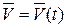 . На рис. 5.10
. На рис. 5.10 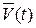 и
и 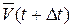 - векторы скорости движущейся точки в моменты t и D t. Чтобы получить приращение вектора скорости
- векторы скорости движущейся точки в моменты t и D t. Чтобы получить приращение вектора скорости 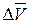 перенесем параллельно вектор
перенесем параллельно вектор 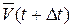 в точку М:
в точку М:
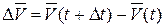
Средним ускорением точки за промежуток времени D t называется отношение приращения вектора скорости 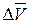 к промежутку времени D t:
к промежутку времени D t:
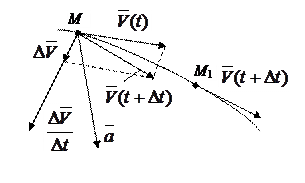 Рис.5.10 Рис.5.10
| 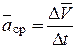 .
Ускорением .
Ускорением 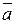 точки в данный момент времени называется предел отношения приращения скорости точки в данный момент времени называется предел отношения приращения скорости 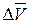 к приращению времени Dt при стремлении последнего к нулю, т.е. к приращению времени Dt при стремлении последнего к нулю, т.е.
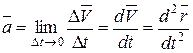 . .
|
Следовательно, ускорение точки в данный момент времени равно первой производной по времени от вектора скорости точки или второй производной радиус-вектора по времени
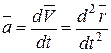 . (5.11)
. (5.11)
Ускорение точки - это векторная величина, характеризующая быстроту изменения вектора скорости по времени.
Построим годограф скорости (рис.5.11). Годографом скорости по определению является кривая, которую вычерчивает конец вектора скорости при движении точки, если вектор скорости откладывается из одной и той же точки.
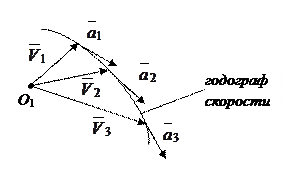 Рис.5.11
Рис.5.11
| Очевидно, что скорость точки, вычерчивающей годограф скорости, будет равна ускорению точки при ее движении по траектории. Единицей измерения ускорения в системе Си является м/с2. |
Определение скорости точки при координатном способе задания её движения
Пусть движение точки задано координатным способом в декартовой системе координат
х = x (t), y = y (t), z = z (t)
Радиус-вектор точки равен
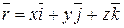 .
.
Так как единичные векторы 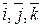 постоянны, то по определению
постоянны, то по определению
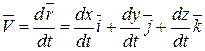 . (5.12)
. (5.12)
Обозначим проекции вектора скорости на оси Ох, Оу и Oz через Vx, Vy, Vz соответственно и разложим вектор скорости по осям:
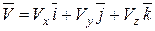 (5.13)
(5.13)
Сравнивая равенства (5.12) и (5.13) получим


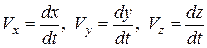 (5.14)
(5.14)
В дальнейшем производную по времени будем обозначать точкой сверху, т.е.
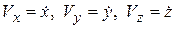 .
.
Модуль скорости точки определяется формулой
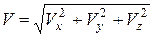 . (5.15)
. (5.15)
Направление вектора скорости определяется направляющими косинусами:
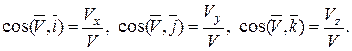
Определение ускорения точки при координатном способе задания её движения
Вектор скорости в декартовой системе координат равен
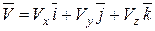 .
.
По определению
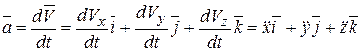 . (5.16)
. (5.16)
Обозначим проекции вектора ускорения на оси Ох, Оу и Oz через аx, аy, аz соответственно и разложим вектор скорости по осям:
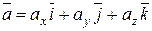 . (5.17)
. (5.17)
Сравнивая равенства (5.16) и (5.17) получим
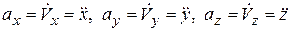 . (5.18)
. (5.18)
Модуль вектора ускорения точки вычисляется аналогично модулю вектора скорости точки:
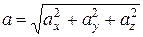 , (5.19)
, (5.19)
а направление вектора ускорения - направляющими косинусами:
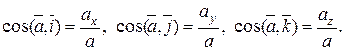
Определение скорости и ускорения точки при естественном способе задания её движения
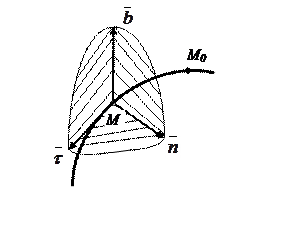 Рис.5.12
Рис.5.12
| При этом способе используются естественные оси с началом в текущем положении точки М на траектории (рис.5.12) и единичными векторами 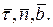 Единичный вектор Единичный вектор 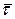 направлен по касательной к траектории в сторону положитель- ного отсчета дуги, единичный вектор направлен по касательной к траектории в сторону положитель- ного отсчета дуги, единичный вектор 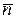 направлен по главной нормали траектории в сторону ее вогнутости, единичный вектор направлен по главной нормали траектории в сторону ее вогнутости, единичный вектор 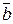 направлен по бинормали к траектории в точке М. направлен по бинормали к траектории в точке М.
|
Орты 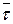 и
и 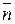 лежат в соприкасающейся плоскости, орты
лежат в соприкасающейся плоскости, орты 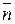 и
и 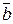 в нормальной плоскости, орты
в нормальной плоскости, орты 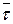 и
и 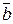 - в спрямляющей плоскости.
- в спрямляющей плоскости.
Полученный трехгранник называется естественным.
Пусть задан закон движения точки s = s (t).
Радиус вектор 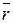 точки М относительно какой-либо фиксированной точки будет сложной функцией времени
точки М относительно какой-либо фиксированной точки будет сложной функцией времени 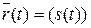 .
.
Из дифференциальной геометрии известны формулы Серре-Френе, устанавливающие связи между единичными векторами естественных осей и вектор-функцией кривой
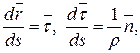
где r - радиус кривизны траектории.
Используя определение скорости и формулы Серре-Френе, получим:
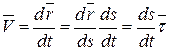 . (5.20)
. (5.20)
Обозначая проекцию скорости на касательную 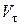 и учитывая, что вектор скорости направлен по касательной, имеем
и учитывая, что вектор скорости направлен по касательной, имеем
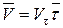 . (5.21)
. (5.21)
Сравнивая равенства (5.20) и (5.21), получим формулы для определения вектора скорости по величине и направлению
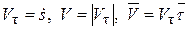 . (5.22)
. (5.22)
Величина 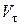 положительна, если точка М движется в положительном направлении отсчета дуги s и отрицательна в противоположном случае.
положительна, если точка М движется в положительном направлении отсчета дуги s и отрицательна в противоположном случае.
Используя определение ускорения и формулы Серре-Френе, получим:
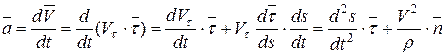 (5.23)
(5.23)
Обозначим проекцию ускорения точки 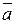 на касательную
на касательную 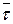 , главную нормаль и бинормаль
, главную нормаль и бинормаль 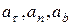 соответственно.
соответственно.
Тогда ускорение равно
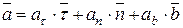 (5.24)
(5.24)
Из формул (5.23) и (5.24) следует, что вектор ускорения всегда лежит в соприкасающейся плоскости и раскладывается по направлениям 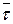 и
и 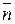 :
:
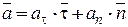 (5.25)
(5.25)
Проекция ускорения на касательную 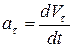 называется касательным или тангенциальным ускорением. Оно характеризует изменение величины скорости.
называется касательным или тангенциальным ускорением. Оно характеризует изменение величины скорости.
Проекция ускорения на главную нормаль 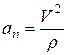 называется нормальным ускорением. Оно характеризует изменение вектора скорости по направлению.
называется нормальным ускорением. Оно характеризует изменение вектора скорости по направлению.
Модуль вектора ускорения равен 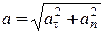 .
.
Если 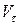 и
и 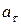 одного знака, то движение точки будет ускоренным.
одного знака, то движение точки будет ускоренным.
Если 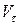 и
и 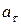 разных знаков, то движение точки будет замедленным.
разных знаков, то движение точки будет замедленным.
|
|
|
|
|
Дата добавления: 2014-01-03; Просмотров: 1457; Нарушение авторских прав?; Мы поможем в написании вашей работы!