Оценка погрешностей многократных измерений

Кроме систематических погрешностей существуют случайные погрешности. Для того чтобы выявить случайную погрешность необходимо повторить измерения несколько раз (многократные измерения).

В преобладающем большинстве случаев различные факторы, вызывающие погрешности измерений, не зависят друг от друга. Погрешность амперметра не зависит от погрешности вольтметра. Погрешность, обусловленная силами трения в рычажных весах, не зависит от погрешности, вызванной неточностью используемых гирь и т.п. Если каждое измерение дает отличные от других результаты, то имеем дело с ситуацией, когда случайная погрешность играет существенную роль.

В теории ошибок показывается, что наиболее близким к истинному значению является среднее арифметическое:

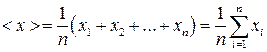(1.7)

где 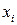- значение измеряемой величины в 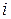-ом опыте, 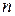- количество измерений. Чем больше 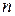, тем точнее 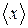приближается к истинному значению измеряемой величины. Однако число измерений всегда конечно и истинное значение 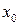остается неизвестным. По теории вероятности среднее арифметическое конечной серии измерений достовернее отдельных измерений, так как случайные отклонения от истинного значения в разные стороны равновероятны. При наличии случайных погрешностей появление того или иного значения 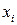в процессе измерения является случайным событием.

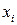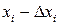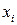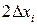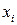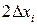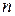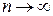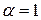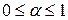Существует некоторая вероятность появления значения в интервале от до . За вероятность () появления величины в интервале шириной принимают относительную частоту появления значения в данном интервале, т.е. отношение числа значений попадавших в интервал к числу всех значений, при числе опытов . Очевидно, что вероятность достоверного события , а невозможного события т.е. или

Доверительным интервалом называют интервал [ 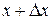; 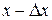], в который по определению попадает истинное значение 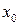измеряемой величины с заданной вероятностью . Доверительной вероятностью , надежностью результата серии измерений, называют вероятность, того что истинное значение 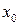измеряемой величины попадает в данный доверительный интервал.

Для серии из 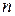опытов случайные погрешности оценивают или по методу "средних", либо методом Стьюдента, связанным с функцией распределения случайных величин, за которые принимаются ошибки отдельных измерений.

В методе «средних»случайная погрешность находится как среднее арифметическое абсолютных значений погрешностей отдельных измерений взятых по модулю:

(1.8)

При этом полная абсолютная погрешность находится как сумма случайной и систематической погрешностей:

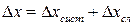(1.8 а)

В методе Стьюдентадля оценки случайной погрешности используется формула:

(1.9)

где 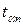- коэффициент Стьюдента, который зависит от заданной вероятности и числа измерений .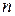

Таблица 1. Коэффициенты Стьюдента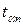

Число измерений	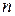Доверительная вероятность (надежность)
90%	95%	99%
	6,314	12,706	63,657
	2,920	4,303	9,925
	2,353	3,182	5,841
	2,132	2,776	4,604
	2,015	2,571	4,032
	1,943	2,447	3,707
	1,895	2,365	3,499
	1,860	2,306	3,355
	1,833	2,262	3,250
	1,812	2,228	3,169
	1,796	2,201	3,106
	1,782	2,179	3,055
	1,771	2,160	3,012
	1,761	2,145	2,977

Для , принятой в данном студенческом практикуме, могут быть использованы приближенные значения соотношений между 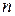и :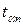

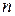
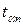
	4,30	3,18	2,78	2,57	2,45	2,36	2,31	2,32

Величину называют среднеквадратичной погрешностью среднего арифметического из серии 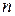измерений.

Полная абсолютная погрешность определяется по формуле:

(1.10)

Дата добавления: 2017-01-14