Выполнение расчетов на ЭВМ

Вопросы

Нет

Нет

Да

? папа(Сережа,Надя) — Сережа — папа Нади?

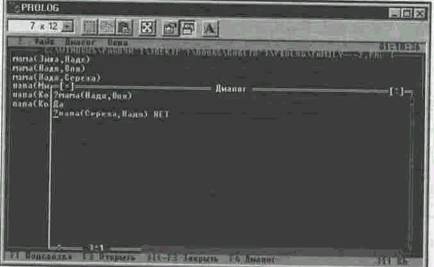
Машина, использующая систему Пролог, дает ответы строго в соответствии с определенными логическими законами и принципами логического вывода. Разберем эти законы и принципы.

Закон противоречия — первый общий закон логики. Этот закон впервые высказал Аристотель - основатель логики как научной дисциплины:

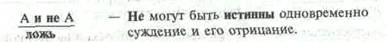
Примеры противоречивых утверждений:

1) «яблоко — спелое»,

«яблоко — неспелое»;

2) «треугольник ABC — прямоугольный»,

«стороны треугольника равны друг другу».

Высказывание противоречивых суждений и утверждений является примером логических ошибок. Наличие противоречий говорит о некотором умысле либо о нарушениях в сознании (базе знаний).

В системе Пролог закон противоречия используется для вывода ответов на вопросы. А именно, каждый вопрос типа? А(х) заменяется на отрицание не А(х) и присоединяется к базе знаний, хранящейся в ЭВМ.

Если получившаяся расширенная база знаний становится противоречивой, то это означает, что утверждение А(х) согласуется с исходной базой знаний и значение переменной х является ответом на заданный вопрос.

Так, вопрос? мама (Надя, Оля) ЭВМ преобразует в отрицание не мама (Надя, Оля) и временно присоединяет его к базе знаний. При этом получившаяся база становится противоречивой и система Пролог объявляет отрицание ложным и выводит ответ ДА.

Закон исключения третьего — второй общий закон логики, указанный Аристотелем:

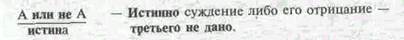
Примеры взаимоисключающих утверждений:

1) «Сегодня будет дождь» и «Сегодня дождя не будет»;

2) «Любой треугольник правильный» и

«В каждом треугольнике есть разные стороны».

Принципы логического вывода в Прологе в отличие от традиционной формальной логики основаны на использовании предикатов. Выражение этого закона Аристотеля на языке предикатов дает конструктивную процедуру вывода конкрентых следствий из общих правил и конкретных фактов.

Закон противоречия в записи на языке исчисления предикатов преобразуется в процедуру вывода ответов на простейшие вопросы вида? А(с):

Содержательный смысл: при противоречии А(х) и не А(с) контрпримером служит х = с. Здесь х — переменная, а с — конкретное значение, при котором отрицание ответа оказывается ложным. Это значение х = с выводится системой Пролог в качестве ответа. Примеры:

? папа(х,Коля) нет — Кто папа у Коли?

? папа(х,Оля) — Кто папа у Оли?

х = Коля

? мама(х,у) — Что известно о мамах?

х = Зина у = Надя

х = Надя у = Оля

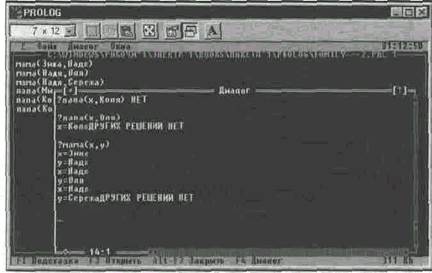
Закон двойного отрицания — третий общий закон формальной логики, указанный Аристотелем:

Примеры рассуждений:

1. Неверно, что «вчера не было дождя».

Следовательно, «вчера был дождь».

2. Неправда, что «это сделал не Саша».

Следовательно, «это сделал Саша». (?)

Из второго примера видно, что закон двойного отрицания является косвенным доказательством, поскольку оно не опирается на факты или аргументы. По этим причинам закон двойного отрицания может оказаться ошибочным и этот закон не является общезначимым (верным для всех случаев и ситуаций).

Правильность утверждений и рассуждений даже при безупречной логике доказательств зависит от достоверности исходных фактов и положений. Эту идею выражает четвертый общий логический закон — закон достаточных оснований, указанный Лейбницем, создателем одного из самых первых механических компьютеров и основателем исчисления предикатов.

Закон достаточных оснований:

Всякое утверждение должно предполагать существование аргументов и фактов, достаточных для его обоснования.

Иными словами, любое утверждение должно предполагать наличие набора фактов и правил, из которых должно вытекать утверждаемое. Нарушениями это закона являются рассуждения, опирающиеся на недостоверные факты или положения, истинность которых не проверяется, а принимается на веру.

Пример рассуждений, не имеющих достаточных оснований:

1.«Если дорогу перебежала черная кошка, то быть неприятностям».

2. «Это верно», потому что«это — справедливо».

Экспертные системы на ЭВМ с этой точки зрения должны создаваться на основе достоверных данных и общих правил вывода, проверенных практикой. Включение недостоверных данных или неподтвержденных обобщений и правил может привести к появлению ошибок и получению неправильных выводов.

Причина такой работы экспертных систем состоит в том, что компьютеры могут делать выводы и умозаключения только исходя из тех фактов и правил, которые введены и хранятся в ЭВМ, и только из этих данных — и ничего другого.

Интеллектуальная мощь экспертных систем на ЭВМ, также как интеллектуальный потенциал людей, связаны с возможностями накопления не только новых конретных фактических сведений, новых обобщенных сведений и знаний.

В базах знаний, экспертных системах и других системах искусственного интеллекта такие знания выражаются в форме новых понятий, записываемых в форме новых правил логического вывода.

В качестве иллюстрации дополним рассмотренную базу знаний о семье набором правил на языке Пролог, выражающих понятие «родитель»:

родитель(х,у) <- мама(х,у); — Мама — родитель.

родитель(х,у) <- папа(х,у); — Папа — родитель.

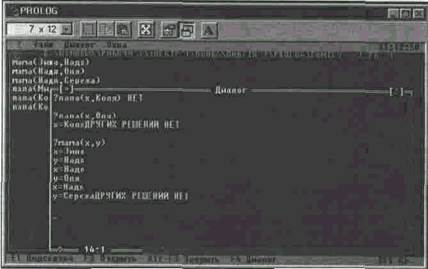
После ввода этих правил в ЭВМ система Пролог на вопросы о родителях выдаст такие ответы при указанной выше базе данных:

? родитель(Надя, х) — Кому родитель Надя?

х = Оля

х = Сережа

Вывод ответов на эти вопросы система Пролог проводит следующим образом. Во-первых, вопрос? родитель(Надя, х) будет заменен на отрицание не родитель(Надя, х). Далее это отрицание будет сопоставлено с правилом вывода родитель(х, у) <— мама(х, у), а затем с правилом родитель(х, у) <- папа(х, у).

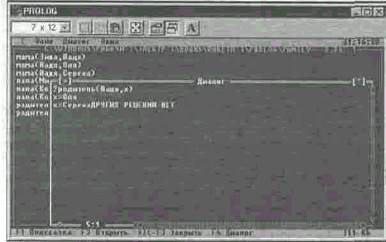
Применение этой же процедуры вывода ко второму определению родитель(х,у) <- папа(х,у) даст отрицание не папа(Надя, х), означающее утверждение «Надя не является папой никому». Для этого утверждения компьютер не имеет в базе данных никаких соответствующих фактов и после просмотра базы знаний по этому варианту выдает ответ НЕТ.

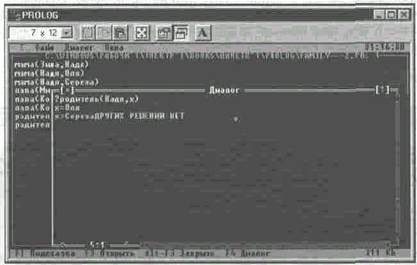
Применение к отрицанию не родитель(Надя, х) и определению родитель(х,у) <- мама(х,у) рассматриваемой процедуры приводит к выводу утверждения не мама (Надя, х), означающему «Надя не является мамой никому».

Для этого отрицания машина найдет два конкретных противоречащих ему факта мама(Надя, Оля) и мама(Надя, Сережа). Используя конструктивную процедуру вывода ответов из отрицаний, компьютер даст два конкретных ответа — х = Оля и х = Сережа.

Закон тождества — четвертый общий логический закон, указанный Аристотелем:

«Предмет рассмотрения должен быть определен и не должен меняться до конца обсуждения».

Данный закон носит фундаментальный характер для работы любых экспертных систем и систем искусственного интеллекта — правильные выводы могут быть получены от таких систем только при строгом совпадении определений вещей из рассматриваемой предметной области.

Расхождения в понимании и определении предметных понятий могут приводитьи, как правило, приводят к логическим ошибкам и получению неправильных выводов и результатов. Это систематически наблюдается среди людей, не обладающих необходимыми профессиональными знаниями.

Примером нарушения закона тождества является подмена предмета, когда два собеседника осознанно или неосознанно говорят о разных вещах, что приводит их к непониманию, спорам и разногласиям. Классический пример нарушения — ситуация: «я — про Фому, а он — про Ерему».

В системе Пролог и в системах искусственного интеллекта вывод ответов на сложные вопросы основан на принципе унификации (взаимосогласования) ответов. Принцип унификации ответов состоит в том, что общие переменные во взаимосвязанных вопросах должны получать одинаковые значения.

Пример ответа на сложносоставной вопрос, состоящий из двух подвопросов:

? мама(z, у), мама(у, Оля) — Кто мама у мамы Оли?

z = Зина

у = Надя

Вывод ответов на сложносоставные вопросы состоит в выделении подвопросов и поиске на них ответов по частям:

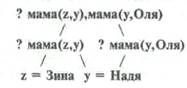
В данном примере общим элементом в выделяемых подвопросах? мама(z,у) и? мама(у,Oля) является переменная «у». Ответом на первый подвопрос? мама(z,у) будут значения z = Зина и у = Надя. Ответы на второй подвопрос? мама(у,0ля) в соответствии с принципом взаимосогласования будет проводиться для значения у = Надя.

Принцип вывода взаимосогласованных ответов в системе Пролог распространяется и на сложносоставные правила, включаемые в базы знаний и процедуры логического вывода. Приведем примеры сложных определений:

бабушка(z, х) <- мама(z, у), мама(у, х);

бабушка(z, х) <- мама(z, у), папа(у, х);

дедушка(z, х) <- nana(z, у), мама(у, х);

дедушка(z, х) <- nana(z, у), папа(у, х).

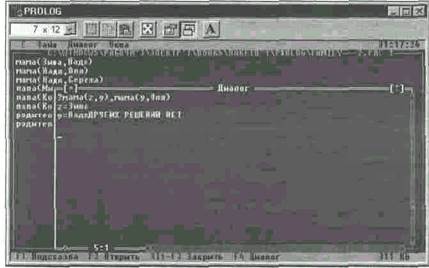
При наличии этих правил в памяти ЭВМ можно получить следующие вопросы о бабушках и дедушках:

? бабушка(z, Оля) — Кто бабушка у Оли?

z = Зина

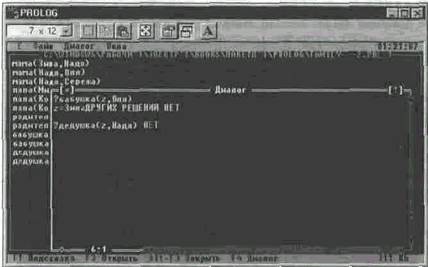
? дедушка(z, Надя) — Кто дедушка у Нади?

Принцип унификации в системе и языке Пролог является общим механизмом логического вывода ответов на сложные вопросы в базах знаний на Прологе и тем самым — конструктивной реализацией закона тождества для машинных систем искусственного интеллекта.

Таким образом, работа экспертных систем на ЭВМ основана строго на выполнении требований законов логики — закона тождества и закона достаточных оснований.

1. В чем состоит закон противоречия?

2. В чем заключается закон исключения третьего?

3. Как используется закон вывода следствий?

4. Как используется закон отрицания следствий?

5. В чем недостатки закона двойного отрицания?

6. В чем состоит закон достаточных оснований?

7. В чем заключается закон тождества?

8. В чем состоит принцип унификации?

9. Как согласуются ответы на сложные вопросы?

Задания

1. Укажите примеры двойного отрицания для утверждений:

а) «сегодня был дождь»; в) «х = 2» и «х = З»;

б) «х = 0» или «у = 0»; г) «5 не делится на 2 и на З».

2. Пусть утверждение А «прошел дождь», а утверждение В «на улице сыро». Истинны ли следующие суждения?

а) А => В (прямое доказательство);

б) В => А (обратное доказательство);

в) не А => не В (противоположное доказательство);

г) не В => не А (противоположное обратному).

3. Предложите систему признаков и понятий для описаний:

а) класса «Млекопитающие»; в) класса «Рыбы»;

б) класса «Птицы»; г) класса «Насекомые».

В систему понятий введите следующие признаки: окрас, продолжительность жизни, умения ползать, летать, ходить и т. д.

4. Составьте базу знаний по всемирной географии. В базу знаний включите сведения о странах: название столицы, число жителей, тип государства, размеры страны, континент.

5. Составьте базу знаний по городам своей страны. В базу знаний включите сведения о размерах городов, числе жителей, расстоянии от столицы, названии самых крупных заводов, фабрик, музеев, стадионов и т. п.

глава 4. Решение задач на ЭВМ

Персональные компьютеры служат удобным средством вычислений и расчетов экономического и математического содержания. В этом смысле компьютеры намного эффективнее бухгалтерских счетов и калькуляторов, которые требуют больших затрат ручного труда.

Наиболее удобным средством проведения расчетов на персональных компьютерах являются электронные таблицы. В этих программах все исходные и расчетные данные отображаются на экране в форме таблиц.

Электронные таблицы — программы для выполнения различных расчетов и хранения всевозможных таблиц с данными. На персональных компьютерах IBM PC наибольшее распространение получили электронные таблицы Excel. В качестве примера рассмотрим калькуляцию закупки сладостей к дню рождения.

Пусть к дню рождения принято решение купить шоколад и конфеты «Аленка», «Мишки», «Марс». Соответствующая калькуляция закупок конфет с учетом их цен, веса и количества имеет вид:

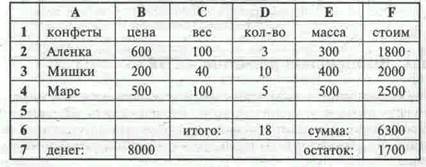
С помощью приведенной электронной таблицы, меняя на экране количество конфет, можно оценить различные варианты закупок. В частности, можно решить следующие проблемы:

купить на заданную сумму наибольшее число сладостей;

купить на заданную сумму наибольшую массу конфет;

купить все виды конфет для пяти гостей в рамках заданной суммы.

Решение. Для расчетов в электронной таблице должна храниться следующая систем формул:

Е2 = C2*D2 F2 = B2*D2

Е3 = C3*D3 F3 = B3*D3

Е4 = C4*D4 F4 = B4*D4

D6 = D2 + D3 + D4 F7 = B7 - F6

F6 = СУММ (F2: F4)

Здесь B2, D3, Е6, F7 — имена ячеек электронной таблицы; СУММ (F2: F4) — функция суммирования ячеек из столбца F от ячейки F2 до ячейки F4.

Основные возможности электронных таблиц:

1) автоматический перерасчет калькуляций;

2) хранение и поиск калькуляций в памяти ЭВМ;

3) вывод калькуляций на печать;

4) обновление и ввод новых калькуляций.

Перерасчет в электронных таблицах производится автоматически сразу же после обновления на экране любых исходных данных. В этом заключается основное свойство и удобство электронных таблиц: один раз составленная калькуляция может использоваться многократно для выполнения расчетов при различных исходных данных.

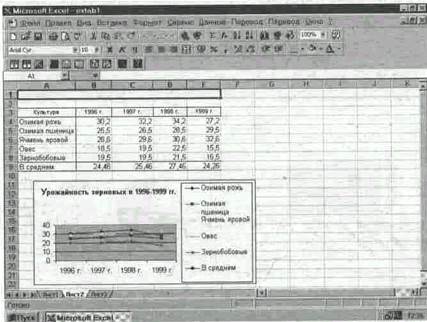
Хранение электронных таблиц обычно проводится на жестких магнитных дисках. Это позволяет использовать их повторно для новых расчетов и перерасчетов. Бумажная копия любой из электронных таблиц со всеми ее исходными и расчетными данными может быть выведена на печать.

Ввод новых таблиц, состоящих из надписей, числовых данных и формул, проводится по ячейкам. Для этого к необходимой ячейке подводится курсор с помощью мышки или клавиш-стрелок, а затем нажимается клавиша Enter на клавиатуре либо клавиша на мышке.

Копирование и перенос надписей, данных, формул и целых блоков позволяет достаточно быстро создавать новые таблицы из уже имеющихся в памяти ЭВМ. Более того, создание новых таблиц обычно осуществляется копированием уже существующих и обновлением в них надписей и данных.

При редактировании таблицы допускается изменение размеров строк или столбцов, а также подбор шрифтов и размера символов для надписей и значений данных, делающие таблицы более наглядными и красиво расположеннными на экране или бумаге.

Для наглядного представления цифровых данных в электронных таблицах обычно предлагается целый набор цветных диаграмм в форме графиков и кругов, а также плоских и объемных гистограмм.

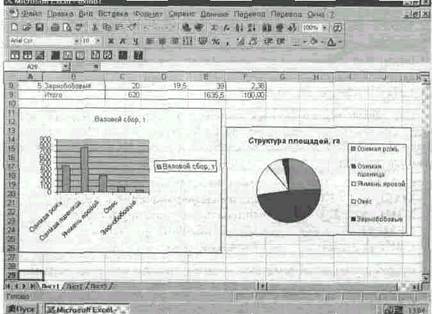
Числовые данные могут быть целыми и вещественными. Примеры записи чисел в электронных таблицах:

0, 1, 2, 3,..., -1, -2, -3,... — целые числа;

0.1, 1.5, 12.87, 0.002,... — вещественные числа.

Обратите внимание: для записи дробной части обычно применяется точка, а не запятая. Для записи десятичного порядка используется символ Е:

1.2Е6 ≡ 1200000;

-.5Е-4 ≡ -0.0005.

Расчетные формулы в электронных таблицах образуются из числовых значений, обозначений элементарных и специальных функций и имен ячеек электронной таблицы: А1, А2, A3, В1, В2, С1 и т.д.

Запись арифметических операций в формулах и числовых выражениях в электронных таблицах выполняется с помощью следующих знаков:

+ — сложение 2 + 2 А2+В2+С2

- — вычитание 6—8 А1—В1

* — умножение 7*8 2*А2*С2

/ — деление 2/3 А1(2/С2)

^ — возведение в степень 5^3 A3^2

Математические функции в электронных таблицах:

sin(x) — синус cos(x) — косинус

tan(x) — тангенс atan(x) — арктангенс

ехр(х) — экспонента ln(x) — натуральный логарифм

sqr(x) — квадратный корень

Для обработки табличных данных в электронных таблицах имеются специальные табличные функции над строками, столбцами и блоками. Приведем наиболее важные и часто употребляемые табличные функции:

СУММ (А2: F4) — сумма чисел в интервале (F2: F4);

МАКС (F2: F4) — максимальное значение в столбце;

МИН (А2: F2) — минимальное значение в строке;

СРЗНАЧ (В2: F4) — среднее значение в интервале;

СЧЕТ (В2: В4) — количество чисел в столбце.

С точки зрения математики — это функции над последовательностями чисел типа (х₁, х₂, …, х_n):

СУММ (х₁, х₂, …, х_n) = х₁ + х₂ +... + х_n;

МАКС (х₁, х₂, …, х_n) = max(х₁, х₂, …, х_n);

МИН (х₁, х₂, …, х_n) = min(х₁, х₂, …, х_n);

СРЗНАЧ (х₁, х₂, …, х_n) = .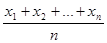

Дата добавления: 2017-01-14