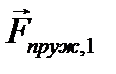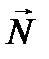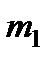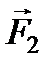Сила пружних деформацій

ПЛАН

САМОСТІЙНА РОБОТА

ВИТЯГ З РОБОЧОЇ НАВЧАЛЬНОЇ ПРОГРАМИ

№ з/п	Назва теми	Кількість годин
	Динаміка матеріальної точки і поступального руху твердого тіла
	Енергія і робота в механіці
	Механіка твердого тіла
	Механіка рідин і газів
	Механічні коливання і хвилі
	Електростатика
	Постійний струм
	Електричний струм в різних середовищах
	Електромагнетизм
	Робота і потужність змінного струму. Трансформація змінного струму. Трансформатор
	Коливальний контур
	Природа світла. Фотометрія
	Геометрична оптика
	Усього 36 годин

3 ЗМІСТ САМОСТІЙНИХ РОБІТ

САМОСТІЙНА РОБОТА № 1 (2 год.)

ТЕМА: Динаміка матеріальної точки і поступального руху твердого тіла.

МЕТА: закріпити знання про динаміку матеріальної точки й поступальний рух твердого тіла, розвивати пізнавальний інтерес, навички творчої роботи.

ПЕРЕЛІК ПОСИЛАНЬ:

1 Бушок Г.Ф.Курс фізики. Кн.1. Фізичні основи механіки. Молекулярна фізика і термодинаміка / Г.Ф. Бушок, Є.Ф. Венгер. – К.: Вища школа, 2002, с. 46-47, с. 50-66.

6 Кучерук І.М. Загальний курс фізики. У трьох томах. Т. 1. Механіка. Молекулярна фізика і термодинаміка / І.М.Кучерук, І.Т Горбачук, П.П. Луцик. – К.: Техніка, 2006, розділи 5, 6.

1 Сила пружних деформацій.

2 Сила тертя.

3 Сила тяжіння. Закон всесвітнього тяжіння.

ЗМІСТ ТЕОРЕТИЧНОГО МАТЕРІАЛУ

Під дією зовнішніх сил виникають деформації (тобто зміни розмірів і форми) тіл. Якщо після припинення дії зовнішніх сил відновлюються попередні форма й розміри тіла, то таку деформацію називають пружною. Деформація має пружний характер у випадку, коли зовнішня сила не перевищує певного значення, яке називається межею пружності. При перевищенні цієї межі деформація стає пластичною. У цьому випадку після усунення зовнішніх сил початкова форма й розміри тіла повністю не відновлюються. Далі ми будемо розглядати тільки пружні деформації.

x

X

x

Рисунок 1

У деформованому тілі виникають пружні сили, які врівноважують зовнішні сили, які викликали деформацію. Пояснимо це таким прикладом (див. рис. 1). Під дією зовнішньої сили 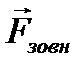пружина отримує видовження 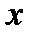, у результаті чого в пружині виникає пружна сила 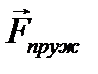, що врівноважує силу .

Пружні сили виникають у всій деформованій пружині. Будь-яка частина пружини діє на іншу частину із силою, що дорівнює 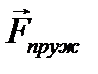(рис.2).

Рисунок 2

Встановлений експериментально закон Гука стверджує, що при пружній деформації видовження пружини пропорційно зовнішній силі. Аналітично цей закон можна записати у вигляді

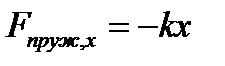, (1.1)

де проекція сили пружності на вісь 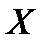(див. рис.1); – деформація (видовження або стиснення) пружини відносно недеформованого стану пружини, – коефіцієнт жорсткості пружини.

Жорсткість 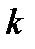пружини залежить від матеріалу, розмірів витка й довжини пружини. Якщо розрізати деформовану пружину на дві однакові частини, пружні сили в кожній із частин залишаться попередніми, а видовження половини пружини буде у два рази менше, ніж у первісної пружини. Звідси згідно (1.1) випливає, що жорсткість «половинної» пружини у два рази більше, ніж цілої.

Однорідні стержні поводяться при розтягуванні й стисненні подібно пружині (рис. 2). Деформація приводить до виникнення у стержні пружних сил. Ці сили прийнято характеризувати напругою , яку визначають як модуль сили, що припадає на одиницю площі:

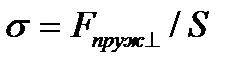(1.2)

( – площа поперечного перерізу стержня; вважаємо, що пружна сила розподілена рівномірно по перетину; значок вказує на те, що сила перпендикулярна до площі, на яку вона діє). У випадку розтягання вважається додатною, у випадку стиснення – від’ємною.

Дослід показує, що збільшення довжини стержня 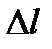пропорційно напрузі та початковій довжині стержня :

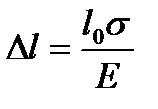(1.3)

Відзначимо, що знак збігається зі знаком . Коефіцієнт 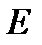у формулі (1.3) характеризує пружні властивості матеріалу стержня. Цей коефіцієнт називають модулем Юнга. Модуль Юнга вимірюється в ньютонах на квадратний метр. Одиниця напруги (а також тиску), що дорівнює ньютону на квадратний метр, називається паскалем (Па).

Рисунок 3

Формулу (3) можна перетворити, позначивши відносне збільшення довжини стержня буквою . У результаті отримуємо остаточну формулу

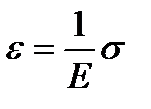, (1.4)

відповідно до якої відносне видовження стержня прямо пропорційно напрузі й обернено пропорційно модулю Юнга. Формула (1.4) виражає закон Гука для стержня.

З (4) випливає, що модуль Юнга дорівнює такій нормальній напрузі, при якому відносне видовження дорівнювало б одиниці (тобто збільшення довжини дорівнювало б початковій довжині 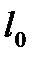стержня), якби настільки великі пружні деформації були можливі. У дійсності, наприклад, залізні стрижні руйнуються при , що дорівнюють приблизно 0,002 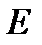; межа пружності досягається при ще менших напругах.

Зазначимо, що розтягання й стиснення стрижнів супроводжується відповідною зміною і їх поперечних розмірів.

2 Сила тертя

Сила тертя спокою 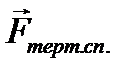виникає під час дії на тіло деякої сили, при якому відносного руху тіла не виникає. Сила тертя спокою однакова за модулем та протилежно направлена до компоненти сили, яка прикладена до тіла та паралельна поверхні дотику тіл. Максимальне значення сили тертя спокою визначається співвідношенням

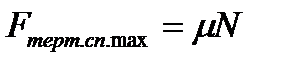, (2.1)

де – модуль нормальної складової сили реакції опори (перпендикулярна до поверхні дотику), що діє на тіло; – коефіцієнт тертя.

У випадку, що зображений на рис. 4, сила тертя спокою (вважаємо, що тіло, яке знаходиться на похилій площині, не рухається), однакова за модулем та протилежно направлена до компоненти сили тяжіння 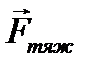, яка паралельна поверхні дотику тіл. Нормальна складова сила реакції опори 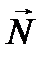теж прикладена до тіла та направлена перпендикулярно до поверхні дотику тіл (див. рис. 4). Слід зазначити, що нормальна складова сили реакції опори разом з силою тертя спокою утворюють повну силу реакції опору 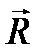: . Сила реакції опори та вага тіла у відповідності до третього закону Ньютона однакові за модулем та протилежні за напрямком: , тобто .

Рисунок 4

Сила тертя ковзання 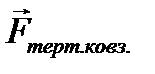виникає під час ковзання тіла по поверхні іншого тіла. Вона направлена протилежно до напрямку вектора відносної швидкості, а її модуль визначається співвідношенням

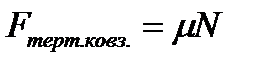, (2.2)

де – модуль нормальної складової сили реакції опори, що діє на тіло, 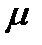– коефіцієнт тертя.

3 Закон всесвітнього тяжіння визначає взаємодію між двома точковими тілами масами 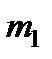та , які розміщені на відстані 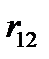один від одного

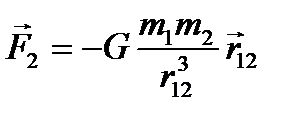. (3.1)

Тут – сила, що діє на точкове тіло масою з боку точкового тіла масою 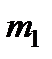(див. рис. 5). Вектор 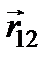з’єднує тіло масою 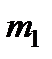з тілом масою . м³/(кг×с²) – універсальна гравітаційна стала. Закон всесвітнього тяжіння можна застосовувати також і до куль. При цьому за відстань між ними потрібно брати відстань між центрами цих куль.

Рисунок 5  

Силою тяжіння називають силу, з якою тіла притягуються до Землі біля поверхні Землі

. (3.2)

Тут маса тіла, – прискорення вільного падіння, яке отримує тіло рухаючись під впливом притягування Землі. Воно однакове для всіх тіл, залежить від географічної широти тіла, його висоти над рівнем моря та інших факторів. Для проведення розрахунків, згідно з рішенням третьої Генеральної конференції з мір та ваг у 1901 році, було прийняте стандартне значення прискорення вільного падіння 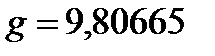м/с², а в технічних розрахунках, як правило, приймають 9,81 м/с². Можна вважати, що вектор прискорення вільного падіння направлений до центру Землі. За своєю природою сила тяжіння відноситься до гравітаційних сил.

Рисунок 6

Вагоютіла називають силу 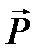, з якою тіло діє на опору або підвіс (див. рис. 6). Вага тіла є різновидом сил пружності. Вагу тіла 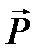потрібно відрізняти від сили тяжіння . Це різні сили за своєю природою, вони прикладені до різних тіл. Сила тяжіння 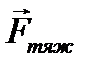діє на тіло, а вага тіла 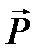діє на опору або підвіс (див. рис. 6).

Силою реакції опори називають силу 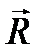, з якою опора або підвіс діють на тіло (див. рис. 6). Слід зазначити що, сила реакції опори 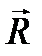та вага тіла 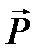однакові за модулем та протилежні за напрямком відповідно до третього закону Ньютона

. (3.3)

Знайдемо вагу тіла для випадку, коли тіло перебуває у стані спокою та коли тіло рухається з прискоренням.

У випадку зображеному на рис. 6 тіло масою знаходиться у спокої відносно Землі. Це означає, що рівнодійна сил, які діють на це тіло дорівнює нулю. На це тіло, як випливає з рисунка, діють дві сили: сила тяжіння 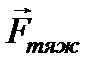з боку Землі та сила реакції опори 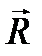. Таким чином,

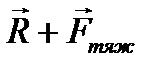=0. (3.4)

Коли взяти до уваги співвідношення (10.3), то з урахуванням (10.4) можемо записати

. (3.5)

Таким чином, вага та сила тяжіння дорівнюють одна одній. Однак слід зазначити, що ці сили прикладені до різних тіл – вага до опори, сила тяжіння до самого тіла.

Рівність (3.5) має місце тільки у тому випадку, коли підвіс або опора (а отже, і тіло) знаходяться у стані спокою відносно Землі (або рухаються без прискорення). Коли опора рухається з прискоренням, вага тіла перестає дорівнювати силі тяжіння.

кабіна ліфта

Рисунок 7

Припустимо, що тіло підвішено до стелі ліфта, який рухається з прискоренням (див. рис.7). З таким же прискоренням рухається і тіло. Тому рівняння руху має вигляд

.

Звідси з урахуванням (3.3) отримуємо

або 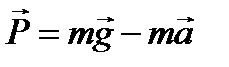. (3.6)

Таким чином отримали формулу (3.6), яка визначає вагу тіла, яке рухається з прискоренням.

Коли б ліфт обірвався й став падати з прискоренням, що дорівнює прискоренню вільного падіння , то тіло б перестало б діяти на підвіс . Про стан, в якому вага тіла дорівнює нулю говорять як про стан невагомості.

ЗАВДАННЯ: законспектувати запитання плану.

Дата добавления: 2017-01-14