Понятие предела последовательности

Введение

Красноярск, 2016 год

Методические указания составлены в соответствии с рабочей программой по дисциплине Элементы высшей математики специальности 38.02.07 Банковское дело.

Составитель: Герман А.В., преподаватель естественно-научных дисциплин ЧПОУ «Красноярский гуманитарно-экономический техникум»

Методические указания и контрольные задания для самостоятельной работы студентов по учебной дисциплине «Элементы высшей математики» (тема «Интегральное исчисление») могут быть использованы в организации учебного процесса в аудиторное и внеаудиторное время для работы над изучением данного материала.

Содержание

1. Введение
2. Содержание темы «Пределы и непрерывность»
2.1. Понятие предела последовательности
2.2. Предел функции
2.3. Раскрытие неопределенности вида о/о
2.4. Раскрытие неопределенности вида
2.5. Замечательные пределы
2.6. Приращение аргумента и приращение функции
2.7. Непрерывность функции
4. Задания для контрольной работы
5. Список используемой литературы

Учебная дисциплина «Элементы высшей математики» является образовательной учебной дисциплиной в цикле математических и общих естественно- научных дисциплин, которая обеспечивает необходимый уровень подготовки специалиста.

Настоящее пособие содержит систематизированное изложение основных понятий теории пределов и непрерывности функций, которые являются одним из разделов курса «Элементы высшей математики», соответствует требованиям Федерального государственного образовательного стандарта среднего профессионального образования по специальности 38.02.07 Банковское дело.

В результате изучения данной темы студент должен:

знать:

– основы теории пределов;

уметь:

– решать прикладные задачи в области профессиональной деятельности.

В пособии представлено достаточное количество примеров, задач, заданий на закрепление изученного материала для самостоятельной работы и вопросов для самоконтроля.

В каждом параграфе приведены краткие теоретические сведения, описаны приемы и образцы вычисления пределов функций, раскрытия неопределенностей различного вида, а затем представлены вопросы для контроля усвоения изученного и задания для самостоятельной работы.

Такая форма изложения позволяет студентам сначала кратко познакомиться с теоретическими фактами, приемами решения типовых задач и оформлением записи их решений, а затем приступить к выработке умений в их самостоятельном решении.

2. Содержание темы «Пределы и непрерывность»

В результате изучения данной темы студент должен:

знать:

- определение предела числовой последовательности и функции, свойства пределов, замечательные пределы;

- определение функции, непрерывной в точке, её свойства;

уметь:

- вычислять пределы последовательностей и функций;

- раскрывать неопределенности;

- классифицировать точки разрыва.

Числовые последовательности. Монотонные, ограниченные последовательности. Предел последовательности, свойства предела. Бесконечно малые и бесконечно большие последовательности, связь между ними, символические равенства. Предел суммы, произведения и частного двух последовательностей. Признак сходимости монотонной последовательности. Число е.

Предел функции. Свойства предела функции. Односторонние пределы. Предел суммы, произведения и частного двух функций. Непрерывные функции, их свойства. Непрерывность элементарных и сложных функций. Замечательные пределы. Точки разрыва, их классификация.

Начальные сведения о пределах встречаются в школь­ном курсе математики. В алгебре с понятием предела свя­зан вопрос о сумме членов бесконечно убывающей гео­метрической прогрессии; в геометрии — вопрос о вычис­лении длины окружности и площади круга, поверхностей и объемов круглых тел.

В курсе математического анализа понятие предела яв­ляется одним из основных. С помощью предела вводятся производная и определенный интеграл; пределы же являются основным средством в построении теории рядов.

Предварительно ознакомимся с понятием числовой последовательности.

Так, например: I) формула а_п – 2n - 1 числам натурального ряда

Пусть каждому натуральному числу п поставлено в со­ответствие число , т. е. пусть задана функция натурального аргумента. Тогда говорят, что задана числовая последовательность Обычно числовую последовательность задают формулой

ставит в соответствие последовательность нечетных чи­сел

2) формула задает числовую последовательность

i

которая является бесконечно убывающей арифметической прогрессией;

3) формула задает возрастающую последовательность

правильных дробей

4) формула задает убывающую последовательность неправильных дробей

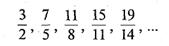
Во всех приведенных примерах заданные последова­тельности являются бесконечными: для каждой из них не существует последнего члена. Вместе с тем сравнение ха­рактера этих последовательностей показывает, что члены первой последовательности по мере увеличения их номе­ра могут стать больше любого произвольно выбранного числа, а члены второй последовательности — меньше лю­бого произвольно выбранного числа. Поэтому первую последовательность называют неограниченно возрастаю­щей, а вторую — неограниченно убывающей. Третья и чет­вертая последовательности являются ограниченными. Чле­ны первой из них, хотя и возрастают с увеличением их номера, но при этом остаются меньше , а члены второй из них, убывая с увеличением их номера, остаются при этом больше

Сравнивая члены третьей последовательности, т. е. значения переменной 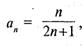с числом мы видим, что с увеличением номера члена разность — по своей абсолютной величине неуклонно убывает и может стать меньше любого наперед заданного положительного числа. Рекомендуется проверить самостоятельно это утвер­ждение, например, взяв

Таким образом, значения переменной т. е. члены третьей последовательности, по мере возрастания номера приближаются к числу так, что абсолютная ве­личина разности становится меньше любого про­извольно выбранного положительного числа. Число 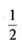называют пределом переменной, или числовой последователь­ности 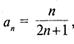, при возрастании аргумента (номера) п. Точно так же для переменной число является пределом, к которому эта переменная стремится, ког­да аргумент возрастает.

Определение. Число А называется пределом последова­тельности а_п, если для любого сколь угодно малого положи­тельного числа (эпсилон) можно указать такой номер N, что при всяком п N абсолютная величина разности меж­ду значением и числом А меньше .

Это кратко записывается так:

если при

Чтобы отметить неограниченный характер изменения аргумента п, когда переменная (функция) стремится к пределу, пишут так:

Приведенное выше определение предела переменной величины (последовательности) не является достаточно общим. Оно предусматривает лишь те случаи, когда аргу­мент принимает целочисленные значения, возрастающие неограниченно Между тем изучаемые в математическом анализе функции могут быть определены на це­лом интервале действительной оси В связи с этим общее определение предела переменной (функции) можно сформулировать так.

Вопросы для самоконтроля:

1. Как можно задать числовую последовательность?

2. Приведите пример неограниченно возрастающей (убывающей) числовой последовательности?

3. Приведите примеры ограниченной числовой последовательности.

4. Дайте определение предела последовательности a _n.

5. Какую краткую запись используют для обозначения предела последовательности?

Дата добавления: 2017-01-14