Непрерывность функции

Пример 4.

Приращение аргумента и приращение функции

Свойства

Первый замечательный предел

Замечательные пределы

Предел отношения sin бесконечно малой величины к самой этой величине равен 1.

Например:

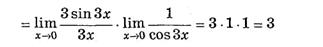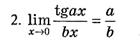
Второй замечательный предел

Например:

	Найдите пределы функций:

Пусть задана некоторая функция и пусть аргумент х при своем изменении принимает одно за другим два значения х, и х_г\ тогда разность х₂ — x_i называется при­ращением аргумента и обозначается символом Ах, т. е.

Греческая буква 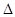(дельта) не является множителем при х, а только указывает на операцию вычитания из нового значения х =х₂ прежнего значения х =х₁. Таким образом, 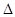неотделима от х, как неотделимы sin от х в выражении sin х или log_a от х в выражении

Разность значений

функции соответствующих значениям х₂ и х₁ аргумента, т. е. разность

называют приращением функции и обозначают символом так что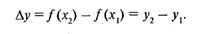

следовательно,

Пусть дана функция у = х₂— Зх. Пусть х_{ = 2 и х₂ = 2,3. Тогда

Если то приращение имеет положительное значение; при приращение будет отрицательным.

Очевидно, и приращение функции может быть вели­чиной как положительной, так и отрицательной.

Вопросы для самоконтроля:

1. Что такое приращение аргумента?

2. Что такое приращение функции?

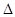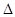3. В чем состоит геометрический смысл приращений x и f?

Понятие непрерывности функции играет исключитель­но важную роль в математическом анализе. В частности, это понятие очень важно и для наших целей, т. е. для на­хождения пределов функций.

Предположим, что рис. 1 дает изображение функции

а рис. 2 — изображение функции

В то время как первая функция изображается нигде не разрывающейся плавной линией, график функций при 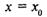имеет разрыв. Вряд ли кому-нибудь будет неясен смысл фразы: «рисунок 1 дает изображение функ­ции, непрерывной при всех значениях х, а рисунок 2 изоб­ражает функцию, имеющую разрыв при (или в точке х = х₀)».

Мы видим, что разрыв функции происходит потому, что при переходе значений аргумен­та через функция изменяется скачком. Переход от

Рис.1 Рис.2

значения к другому значению х можно представить так, что значению х₀ придано приращение Тогда новое значение функции будет разниться от старого на приращение

Мы видим (рис. 2), что когда приращение оставаясь положительным, уменьшается и приближается к 0, то приращение функции приближается к значению, рав­ному длине отрезка MN. Если бы приращение стреми­лось к нулю, то ясно, что функция при

не имела бы разрыва.

После приведенных наглядных соображений, дающих представление о понятии непрерывности функции в точ­ке, дадим точное определение этого понятия.

Будем называть окрестностью точки х₀ любой проме­жуток, содержащий точку х₀ внутри себя.

Дата добавления: 2017-01-14