
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Домашняя контрольная работа. Задания для контрольной работы
|
|
|
|
Задания для контрольной работы
Определение.
Функция

называется непрерывной в точке х0, если:
1) она определена в некоторой окрестности этой точки;
2) предел приращения  функции у, вызываемого приращением
функции у, вызываемого приращением 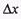 аргумента х, равен нулю при
аргумента х, равен нулю при 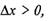 т. е.
т. е.

Другими словами, функция  называется непрерывной в точке х0, если она определена в некоторой окрестности этой точки и если приращение ее
называется непрерывной в точке х0, если она определена в некоторой окрестности этой точки и если приращение ее 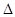 у при
у при 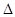 х -> О есть величина бесконечно малая.
х -> О есть величина бесконечно малая.
Если условие непрерывности функции в точке х0 нарушено, то говорят, что в этой точке функция имеет разрыв (или претерпевает разрыв) и точку х0 называют точкой разрыва функции.
Итак, если приращение 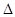 у функции при
у функции при 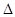 х —» О есть величина бесконечно малая, то функция у = f(x), по определению, в точке хп непрерывна. Так как
х —» О есть величина бесконечно малая, то функция у = f(x), по определению, в точке хп непрерывна. Так как 
то, следовательно, при 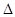 х —> 0 разность между переменной величиной
х —> 0 разность между переменной величиной  и числом
и числом  есть величина бесконечно малая. Отсюда, по определению предела, заключаем, что
есть величина бесконечно малая. Отсюда, по определению предела, заключаем, что


 |
т. е. если функция у = Дх), определенная в некоторой окрестности точки х0, непрерывна в точке х0, то предел ее при х ® х0 равен значению функции при х =х0.
Обратно, пусть известно, что
 (7)
(7)
Тогда разность

есть величина бесконечно малая при х®х0. Но эта разность есть приращение 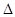 у функции, отвечающее приращению
у функции, отвечающее приращению 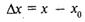 аргумента. Когда
аргумента. Когда  Итак, если имеет место равенство (7), то
Итак, если имеет место равенство (7), то  т. е. функция у = f (х) в точке х0 непрерывна.
т. е. функция у = f (х) в точке х0 непрерывна.
Из доказанных предложений следует, что данное выше определение непрерывности функции в точке может быть заменено таким определением:
Функция  называется непрерывной в точке х0, если она определена в некоторой окрестности этой точки и если
называется непрерывной в точке х0, если она определена в некоторой окрестности этой точки и если

Среди функций, с которыми мы встречались ранее, имеются функции непрерывные и разрывные.

 Функции
Функции  определены на всей числовой оси, кроме точки
определены на всей числовой оси, кроме точки 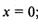 ; в этой точке выражения
; в этой точке выражения  и
и  теряют смысл (деление на нуль невозможно). Условие (8) непрерывности
теряют смысл (деление на нуль невозможно). Условие (8) непрерывности  функции в точке
функции в точке  требует, чтобы функция была определена в некоторой окрестности точки х0, а потому и в самой точке
требует, чтобы функция была определена в некоторой окрестности точки х0, а потому и в самой точке  Так как рассматриваемые функции в точке 0 не определены, то они претерпевают разрыв в этой точке. При
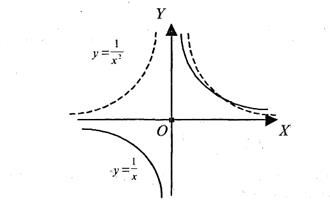
Так как рассматриваемые функции в точке 0 не определены, то они претерпевают разрыв в этой точке. При  эти функции суть величины бесконечно большие. Графики их изображены на рис. 47. Мы видим, что каждый из графиков состоит из двух отдельных ветвей; это служит наглядной иллюстрацией того, что точка есть точка разрыва рассматриваемых функций.
эти функции суть величины бесконечно большие. Графики их изображены на рис. 47. Мы видим, что каждый из графиков состоит из двух отдельных ветвей; это служит наглядной иллюстрацией того, что точка есть точка разрыва рассматриваемых функций.
|
Если функция непрерывна в каждой точке отрезка [a,b] или промежутка (а, b), то говорят, что она непрерывна на отрезке [а, b] или соответственно в промежутке (а, b).
Так, функция  непрерывна в промежутке
непрерывна в промежутке 
Функции  непрерывны на любом отрезке, не содержащем точку х = 0.
непрерывны на любом отрезке, не содержащем точку х = 0.
Функция 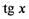 непрерывна при всех значениях х, кроме значений
непрерывна при всех значениях х, кроме значений  в точках
в точках 
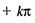 нарушается условие непрерывности, так как в этих точках функция
нарушается условие непрерывности, так как в этих точках функция  не определена. По этой же причине функция
не определена. По этой же причине функция  имеет разрывы в точках
имеет разрывы в точках 
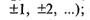 при всех же остальных значениях функция ctg х непрерывна.
при всех же остальных значениях функция ctg х непрерывна.
В полных курсах математического анализа подробно рассматривается вопрос о непрерывности функций, с которыми имеет дело анализ. Здесь мы лишь кратко укажем, что все функции, с которыми будем встречаться в дальнейшем, непрерывны всюду, за исключением отдельных точек.
Непрерывность функции  в точке с определяется соотношением
в точке с определяется соотношением

Отсюда следует, что для нахождения предела при х ® с функции, непрерывной в точке с, достаточно вычислить ее значение при х — с: получающееся при этом число и есть искомый предел функции.
Таким образом, например, находим:


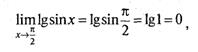
и т. п.
Вместе с тем такая простота нахождения пределов непрерывных функций позволяет в ряде случаев достаточно легко находить и пределы функций, не являющихся непрерывными в данной точке.
Пусть, например, требуется найти

В точке  функция
функция  имеет разрыв:
имеет разрыв: 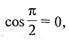 и так как деление на нуль невозможно, то при
и так как деление на нуль невозможно, то при  дробь
дробь  теряет смысл; другими словами, рассматриваемая функция вовсе не определена в точке
теряет смысл; другими словами, рассматриваемая функция вовсе не определена в точке  а потому имеет разрыв в этой точке. Но при
а потому имеет разрыв в этой точке. Но при  значение
значение  из рассмотрения исключается;
из рассмотрения исключается;  и выражение
и выражение 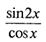 можно сократить на
можно сократить на 

Отсюда следует, что функция  и
и  изменяются одинаковым образом. Функция
изменяются одинаковым образом. Функция 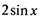 непрерывна в точке
непрерывна в точке  поэтому
поэтому 
Следовательно, и 
Подобным же образом находим:


Вопросы для самоконтроля:
1. Приведите примеры известных элементарных функций, являющихся непрерывными при всех значениях x, и примеры функций, имеющих разрыв в какой либо точке.
2. Дайте определения функции, непрерывной в точке.
3. Что такое окрестность точки x0?
4. Дайте определение функции, непрерывной на отрезке.
5. Правило нахождения пределов непрерывных функций и пределов функций, не являющихся непрерывными в данной точке.
1 вариант
1. Найдите пределы функций
а) с б) 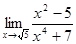 ; в)
; в)  ; г)
; г)  ;
;
д) 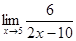 ; е)
; е)  ; ж)
; ж)  ; з)
; з)  .
.
2. Найдите производную функций
а)  ; б)
; б)  ; в)
; в) 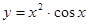 ; г)
; г)  ;
;
д)  ; е)
; е)  ; ж)
; ж)  ; з)
; з)  .
.
3. Найдите производные второго порядка для указанных функций
а)  ; б)
; б) 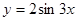 ; в)
; в)  .
.
4. Найдите экстремумы функции, используя производную второго порядка

5. Найдите промежутки выпуклости и вогнутости функции

2 ВАРИАНТ
1. Найдите пределы функций
а)  ; б)
; б)  ; в)
; в) 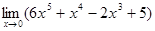 ; г)
; г) 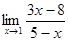 ;
;
д)  ; е)
; е)  ; ж)
; ж)  ; з)
; з) 
2. Найдите производную функций
а) 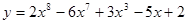 ; б)
; б)  ; в)
; в)  ; г)
; г)  ;
;
д)  ; е)
; е)  ж)
ж) 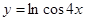 ; з)
; з)  .
.
3. Найдите производные второго порядка для указанных функций
а)  ; б)
; б)  ; в)
; в)  .
.
4. Найдите экстремумы функции, используя производную второго порядка

5. Найдите промежутки выпуклости и вогнутости функции

|
|
|
|
|
Дата добавления: 2017-01-14; Просмотров: 145; Нарушение авторских прав?; Мы поможем в написании вашей работы!