Построение графиков линейной функции, содержащих переменную под знаком модуля

ЛИНЕЙНАЯ ФУНКЦИЯ

Алгоритм решения неравенств, содержащих модули.

Рассмотрим несколько видов неравенств, содержащих модули:

1.

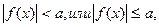
1) а < 0 неравенство не имеет решений;

2) а = 0 первое неравенство не имеет решений, а второе: ;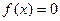

3) а > 0 неравенство равносильно системе неравенств:

,

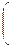
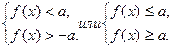
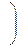
2.

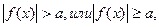
1) а < 0 решением неравенства является любое действительное число;

2) а = 0, решением неравенства является любое действительное число, кроме 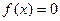(или любое действительное число);

3) а > 0 неравенство равносильно совокупности неравенств:

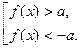
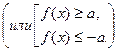
3. 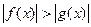, 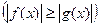или , .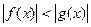

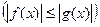1) возвести обе части неравенства в квадрат: ;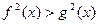

2) разложить разность квадратов на множители: ;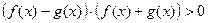

3) решить полученное неравенство методом интервалов.

4. 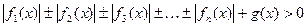или 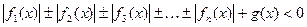, решают методом разбиения на промежутки:

1) находят значения переменной, при которых входящие в неравенство модули равны нулю (нули модулей);

2) область определения неравенства разбивают этими значениями на промежутки и по определению модуля, определяют знаки модуля на полученных промежутках;

3) на каждом из полученных промежутков раскрывают модули и получают неравенство: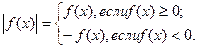

4) решают каждое неравенство;

5) полученные решения сравнить с данным промежутком и вывести общее решение;

6) объединить решения, полученные на всех промежутках.

Для построения графиков линейной функции, содержащих переменную под знаком модуля, рассмотрим несколько случаев:

а) 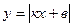: строим 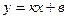и отображаем часть графика расположенную ниже оси Ох, вверх, относительно оси Ох.

Пример 1: построить график функции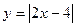

Построение: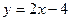

х
у	– 4

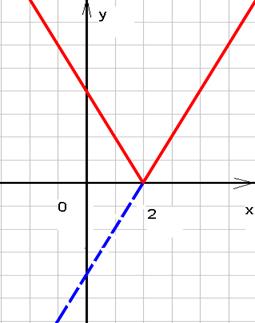
Пример 2: построить график функции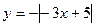

Построение:

х
у		– 1

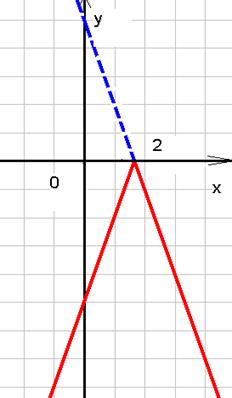
б) построение графиков с помощью разбиения на промежутки.

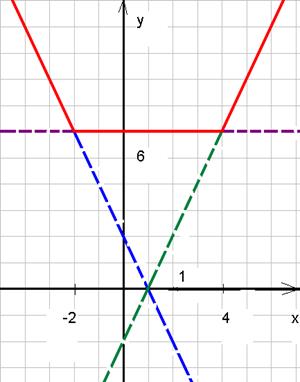
Пример 3: построить график функции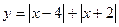

Построение: х – 4 = 0 х + 2 = 0

х = 4 х = – 2

1) 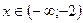: у = – х + 4 – х – 2, у = – 2 х + 2.

2) 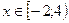: у = – х + 4 + х + 2, у = 6.

3) 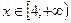: у = х – 4 + х + 2, у = 2 х – 2

Пример 4: построить график функции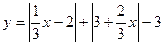

Построение: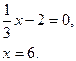

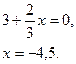
1) : ;

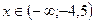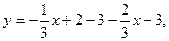
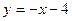2) :

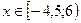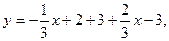
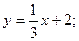
3) : .

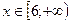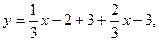
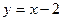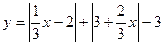
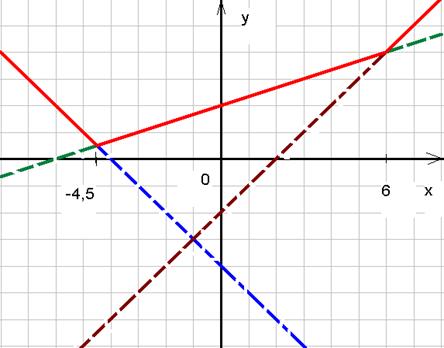
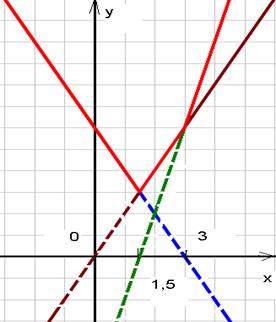
Пример 5: построить график функции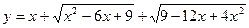

Построение: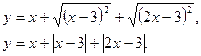

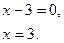
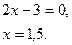
1) : ;

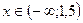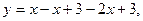
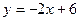2) : ;

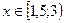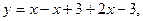
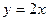3) : , .

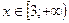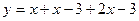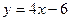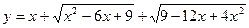
в) построение графиков с двойными модулями.

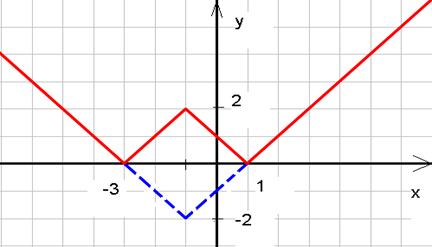
Пример 6: построить график функции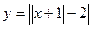

Построение: 1) строим график функции ;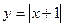

2) построенный график опускаем на 2 единицы вниз;

3) отображаем часть графика расположенного ниже оси Ох, вверх относительно оси Ох.

Дата добавления: 2017-01-14