Системы линейных алгебраических уравнений. 6 страница

Направляющими косинусами вектора называются косинусы углов, образуемых им с координатными осями.

Скалярным произведением двух векторов называется число, равное произведению длин векторов на косинус угла между ними

Для скалярного произведения справедливо:

1.

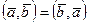
2.

3.

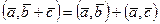
Из этих свойств следует, что при скалярном умножении можно раскрывать скобки так же, как при умножении многочленов.

Через координаты скалярное произведение представляется следующим образом:

Необходимым и достаточным условием перпендикулярности ненулевых векторов и 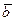является равенство нулю их скалярного произведения.

Кроме того используя скалярное произведение становиться возможным находить угол между векторами где φ угол между векторами и .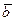

Векторным произведением векторов и 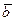называется вектор , определяемый следующим образом:

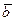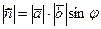^ , ^ ; ; вектора , 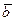и образуют правую тройку

Векторное произведение обозначается символами = ´ =[ , ]

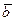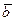Для векторного произведения справедливо:

1.

2.

3.

Через координаты векторное произведение представляется следующим образом:

Необходимым и достаточным условием коллинеарности ненулевых векторов и 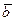является равенство нулю их векторного произведения.

Кроме того используя векторное произведение становиться возможным находить площадь параллелограмма и площадь треугольника построенного на этих векторах: S_□= ;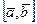

Смешанным (векторно-скалярным) произведением трех векторов , 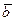и называется число равное (, , )=([ , ], )

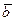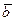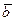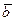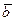Смешанное произведение (, , ) с точностью до знака равно объему параллелепипеда, построенного на векторах , , . Произведение имеет знак (+), если тройка , , - правая, (-) - если тройка , , 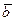- левая.

Необходимым и достаточным условием компланарности трех ненулевых векторов , , 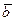является равенство нулю их смешанного произведения.

Через координаты смешанное произведение представляется следующим образом: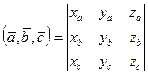

Системой m линейных алгебраических уравнений (СЛАУ) с n неизвестными будем называть следующую систему:

где x_j, j= -неизвестные; а _ij, -коэффициенты при неизвестных; b_i, - свободные члены. При b_i=0, , система называется однородной.

Решением системы называется такая совокупность чисел 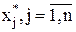, которая при подстановке вместо в каждое уравнение системы обращает его в тождество.

СЛАУ называется совместной, если она имеет решение, несовместной - если решения нет

Однородная система всегда совместна, т.к. имеет нулевое решение.

Совместная система называется определенной, если она имеет единственное решение, неопределенной - если решений бесконечное множество.

Две совместные системы называются равносильными, если все их решения совпадают.

Коэффициенты при неизвестных в системе составляют прямоугольную таблицу - матрицу A_mn из m строк и n столбцов, она называется основной матрицей системы, а матрица (А\В) - расширенной:

.

Строки и столбцы матрицы можно воспринимать как вектора.

Рангом матрицы А (обозначается rgA) называется максимальное число линейно-независимых строк матрицы.

Теорема Крониккера-Капелли. Система линейных уравнений совместна тогда, когда rang(A)=rang(A\B).

В случае если матрица системы представляет из себя, не вырожденную квадратную матрицу, то возможны три метода ее решения.

Матричный метод.

Исходную систему уравнений можно представить в виде , где . Таким образом, вектор столбец переменных представляет из себя произведение обратной матрицы к матрице системы на вектор столбец свободных членов.

Метод Крамера.

Неизвестные системы определяют по формулам: Где D - определитель исходной матрицы системы, а D_j определитель получается из определителя D заменой j-го столбца столбцом свободных членов.

Метод Гаусса.

Данный метод заключается в последовательном исключении неизвестных из уравнений системы путем элементарных преобразований над расширенной матрицей.

Процесс продолжаем, пока не получим треугольную матрицу.

Из последней строки определим x_n, зная значение этой переменной из предпоследней строки определим значение x_n-1, …

Данный метод легко обобщаем на случай когда число переменных не равно числу уравнений.

Также при помощи элементарных преобразований приводим расширенную матрицу к ступенчатому виду

(A\B)~ ,

причем rg(A\B) равен числу ненулевых строк в ступенчатой матрице.

Возможны три случая:

1. Получилась строка (0 0...0| b_k ¢¢), b_k ¢¢¹0, ей соответствует уравнение

0= b _k¢¢ - система несовместна (rgA¹ rg(A\B)).

2. Число ненулевых строк r меньше числа неизвестных, тогда система имеет бесчисленное множество решений. Последней ненулевой строке соответствует уравнение a_rr ¢¢x_r +...+ a_rn ¢¢x_n= b_r ¢¢, из которого находим неизвестное x_r через n-r так называемых свободных неизвестных: x_r+1,...., x_n. Из уравнений, соответствующих другим строкам, последовательно находим x₁,..., x_r-1 также через свободные неизвестные.

3. r=n - решение системы единственно. Последней ненулевой строке соответствует уравнение a_nn ¢¢x_n = b_n ¢¢, из которого находим неизвестное х_n, а далее последовательно - x₁, x₂,..., x_n-1.

Дата добавления: 2017-01-14