Аналитическая геометрия

Пусть на плоскости выбрана прямоугольная система координат.

Линия на плоскости может быть задана характерными геометрическими свойствами, по которым находится ее уравнение. Координаты произвольной точки линии являются текущими координатами этой точки, или при помощи уравнения.

Уравнение F(x,y) = 0 называется уравнением линии на плоскости, если ему удовлетворяют координаты (x,y) каждой точки данной линии и не удовлетворяют координаты точек, не лежащих на ней.

Прямая на плоскости в декартовой прямоугольной системе координат Оxy может быть задана уравнением одного из следующих видов.

1. – общее уравнение прямой.

2. – уравнение прямой, проходящей через точку перпендикулярно нормальному вектору .

3. – уравнение прямой, проходящей через точку параллельно направляющему вектору (каноническое уравнение прямой).

4. – уравнение прямой, проходящей через точку параллельно направляющему вектору (параметрическое уравнение прямой).

5. – уравнение прямой в отрезках, где a и b – величины направленных отрезков, отсекаемых прямой на координатных осях.

6. – уравнением прямой с угловым коэффициентом k, где k – тангенс угла между прямой и положительным направлением оси абсцисс.

7. 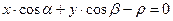– нормальное уравнение прямой, где , – направляющие косинусы нормального вектора 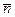направленного из начала координат в сторону прямой, – расстояние от начала координат до прямой.

Общее уравнение прямой приводится к нормальному виду путем умножения его на нормирующий множитель 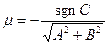, где .

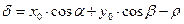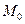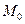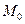Если прямая L задана своим нормальным уравнением, а – некоторая точка плоскости, то выражение задает отклонение точки от прямой L. Знак отклонения указывает на взаимное расположение точки и начала координат относительно прямой L: точка и начало координат лежат по разные стороны относительно прямой L; точка 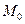и начало координат лежат по одну сторону относительно прямой L; точка 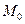лежит на прямой L.

Расстояние от точки 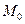до прямой L равно модулю отклонения .

Если две прямые L₁ и L₂ заданы уравнениями с угловыми коэффициентами, то тангенс угла между ними может быть определен по формуле: .

Достаточно часто рассматривается уравнение прямой на плоскости проходящей через две точки и , оно имеет вид:

Аналогично линиям на плоскости поверхности могут быть заданы характерными геометрическими свойствами или при помощи уравнений.

Уравнение F(x,y,z)=0 называется уравнением поверхности, если ему удовлетворяют координаты (x,y,z) каждой точки данной поверхности и не удовлетворяют координаты точек, не лежащих на ней.

Плоскость в пространстве в декартовой прямоугольной системе координат Оxyz может быть задана уравнением одного из следующих видов.

1. 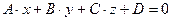– общее уравнение плоскости.

2. 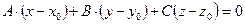– уравнение плоскости, проходящей через точку 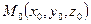перпендикулярно нормальному вектору .

3. – уравнение плоскости в отрезках, где a, b и c – величины направленных отрезков, отсекаемых прямой на координатных осях.

4. – нормальное уравнение плоскости, где , , – направляющие косинусы нормального вектора 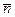направленного из начала координат в сторону плоскости, – расстояние от начала координат до плоскости.

Общее уравнение плоскости приводится к нормальному виду путем умножения его на нормирующий множитель .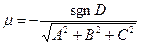

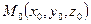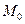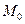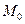Если плоскость P задана своим нормальным уравнением, а – некоторая точка прастранства, то выражение задает отклонение точки от плоскости P. Знак отклонения указывает на взаимное расположение точки и начала координат относительно плоскости P: точка и начало координат лежат по разные стороны относительно плоскости P;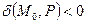 точка 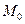и начало координат лежат по одну сторону относительно плоскости P; точка 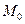лежит на плоскости P.

Расстояние от точки 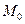до плоскости P равно модулю отклонения .

Часто рассматривается уравнение плоскости проходящей через три точки , 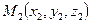и оно имеет вид:

Линию в пространстве можно всегда определить как линию пересечения двух поверхностей. Если они заданы уравнениями F₁(x,y,z)=0 и F₂(x,y,z)=0, то система этих уравнений задает уравнения линии пересечения поверхностей.

Прямая в пространстве может быть задана при помощи уравнения одного из следующих видов:

1. – общее уравнение прямой.

2. 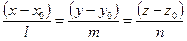– уравнение прямой, проходящей через точку 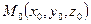параллельно направляющему вектору (каноническое уравнение прямой).

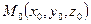3. – уравнение прямой, проходящей через точку параллельно направляющему вектору (параметрическое уравнение прямой).

Достаточно часто рассматривается уравнение прямой в пространстве проходящей через две точки и 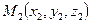, оно имеет вид:

Математический анализ

Множеством называют совокупность элементов объединенных, каким либо общим свойством. Множества обозначаются заглавными буквами X, Y, A, B; их элементы - строчными x, y, a, b; xÎX - означает, что элемент х принадлежит множеству Х, хÏХ - не принадлежит; АÌВ - множество А состоит из части элементов множества В, т.е. является подмножеством В.

Множества А и В называют равными, если АÌВ и ВÌА.

Объединением АÈВ множеств А и В называется множество, состоящее из элементов, входящих или в А или в В; пересечением АÇВ называется множество, состоящее из элементов, входящих в А и в В; разностью А\В множеств А и В называется подмножество множества А элементов, не входящих в В. Если ВÌА, то`В=А\В называется дополнением множества А до множества А

Пустое множество (множество, не содержащее ни одного элемента) обозначается символом Æ.

Считают, что между множествами Х и Y установлено соответствие (обозначение X Y), если для любого xÎX указаны соответствующие ему yÎY.

Соответствие между X и Y называется взаимно-однозначным, если для любого xÎX существует единственный элемент yÎY и наоборот, для любого yÎY существует единственный элемент xÎX (обозначение Х Y).

Два множества X и Y называются эквивалентными или имеющими одинаковую мощность (X~Y), если между ними можно установить взаимно-однозначное соответствие.

Множество, эквивалентное множеству натуральных чисел, называется счетным.

Для сокращения записи математических высказываний употребляется символика математической логики. Пусть a, b - некоторые высказывания, относительно которых можно сказать, истинны они или ложны.

Запись `a означает “не a“, т.е. отрицание a;

aÞb - “из a следует b“ (Þ - символ импликации);

aÛb - “a эквивалентно b“ (Û - символ эквивалентности);

aÙb - “ a и b“ (Ù - символ конъюнкции);

aÚb - “ a или b“ (Ú - символ дизъюнкции);

"xÎA - “для любого xÎA” (" - квантор всеобщности);

$ yÎB - “существует yÎB” ($ - квантор существования);

" xÎA: a - “для любого х из А имеет место a“;

$! xÎХ - “существует единственный х из Х”.

d - окрестностью U_d(a) точки а Î R называется интервал (а -d, а +d) (d>0), dÎR. Проколотой d - окрестностью U_d(a) называется множество U_d(a)\{ a }

Точка а ÎА называется внутренней точкой множества А, если $(d>0: U_d(a)ÌА. Множество А называется открытым, если оно состоит из внутренних точек.

Функцией y=f(x), определенной на множестве Х и принимающей значения на множестве Y, называется такое соответствие между этими множествами, при котором для каждого xÎХ существует единственный элемент yÎY: y=f(x), xÎХ, yÎY ÛX Y: " xÎХ$! yÎY

Функция y=f(x) называется возрастающей на [ a,b ], если большему значению аргумента соответствует большее значение функции: x₁<x₂, x₁,x₂Î[ a,b ] Þ f(x₁)<f(x₂), убывающей на [ a,b ], если x₁<x₂, x₁,x₂Î[ a,b ] Þ f(x₁)>f(x₂). Функция только возрастающая или убывающая на [ a,b ], называется монотонной.

Функция x=f^-1(y) называется обратной к функции y=f(x), устанавливающей взаимно-однозначное соответствие между X=D(f) и Y=E(f) (), если x=f^-1(y) выражает то же соответствие, причем Y=D(f^-1), X=E(f^-1)

Сложной функцией y=j[y(x)] (или суперпозицией) называется такая функция, для которой: y=j(z), yÎY, zÎZ, z=y(x), xÎX, zÎZ Þy=(j_°y)x.

Последовательностью называется числовая функция, определенная на множестве N натуральных чисел, т.е. x_n=f(n).

Дата добавления: 2017-01-14