Теория пределов

Число a называется пределом последовательности x_n при неограниченном возрастании n (a = ), если для любого числа e>0 найдется номер N, зависящий только от e и такой, что при n³N(e) выполняется неравенство |x_n- a |<e

Символическая запись определения:

Число b называется пределом функции y=f(x) при х® a, если для любого числа e>0 существует такое число d, зависящее только от e, что из неравенства 0<|x - a |<d следует неравенство |f(x) - b |< e.

Символическая запись определения:

Аналогично определению предела последовательности можно ввести и предел функции при х®¥.

Теоремы о правилах предельного перехода.

Предел постоянной равен самой постоянной.

Для того чтобы 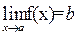, необходимо и достаточно выполнение равенства f(x)= b + a(x), где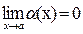

Предел суммы конечного числа функций, имеющих пределы при x® a, равен сумме их пределов

Предел произведения конечного числа функций, имеющих пределы при x® a равен произведению пределов

Постоянный множитель можно выносить за знак предела.

Предел отношения двух функций, имеющих пределы при x® a, равен отношению их пределов (если предел знаменателя не нуль).

Если j(x)£f(x)£y(x) в окрестности т. а и 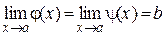, то и

Основные теоремы о пределах облегчают нахождение пределов. В простейших случаях оказывается достаточным подставить в функцию предельное значение аргумента. Если же при такой подстановке получается неопределенное выражение вида , то нахождение предела для таких случаев называют раскрытием неопределенности.

При раскрытиях неопределенностей используются методы вынесения общего множителя за скобку и его сокращение (причем за скобку стремятся вынести такой множитель после сокращения которого предел считается простой подстановкой).

Кроме того в некоторых случаях неопределенности раскрываются с использованием так называемых I и II замечательных пределах.

I замечательный предел:

II замечательный предел: .

е»2,71828... Логарифмы чисел по основанию е обозначаются lnx и называются натуральными логарифмами.

Пусть функция y=f(x) определена в т. x₀ и ее окрестности: y₀=f(x₀). Если аргумент x получит приращение Dx в т. x₀, т.е. x=x+Dx-новое значение, то и функция получит приращение Dy. Новое значение функции будет y₀+Dy=f(x₀+Dx), а приращение функции в т.x₀ Dy= f(x₀+Dx)-f(x₀)

Функция y=f(x) называется непрерывной в т.x₀, если: она определена в т. х₀ и ее окрестности; .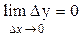

Функция y=f(x) называется непрерывной на множестве Х, если она непрерывна в каждой точке этого множества.

Точка х₀ называется точкой разрыва функции y=f(x), если функция не является непрерывной в т. х₀

Предел 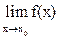, если х®х₀, оставаясь меньше х₀, называется левосторонним пределом и обозначается, предел при х®х₀, х>х₀, называется правосторонним пределом и обозначается ·

Точки разрыва бывают трех типов:

1) х₀- устранимая т.р. Û$f(x₀-0)=f(x₀+0) и они конечны, но f(x₀) $.

2) х₀ - т.р. 1 рода f(x₀+0), f(x₀-0) - конечны, но f(x₀+0)¹f(x₀-0).

3) х₀ - т.р. 2 рода: все остальные т.р.

Если функция f(x) непрерывна на [ a,b ], то она достигает на [ a,b ] своего наибольшего М и наименьшего m значений (m£f(x)£M), т.е. непрерывная на [ a,b ] функция ограничена на [ a,b ].

Если функция) непрерывна на [ a,b ] и на концах [ a,b ] принимает значения разных знаков, то $cÎ[ a,b ], в которой f(c)=0

Если f(x)Î) непрерывна на [ a,b ], f(a)¹f(b), то для любого числа m между f(a) и f(b) найдется т. xÎ (a,b), в которой f(x)=m.Таким образом, непрерывная функция на [ a,b ] принимает все свои промежуточные значения.

Дата добавления: 2017-01-14