Геометрические тела с поперечным отверстием

Поперечными называют отверстия, направленные перпендикулярно к длине или высоте предмета.

В данной теме рассматриваются геометрические тела, имеющие сквозные поперечные отверстия — окна и вырезы, ограни­ченные отсеками плоскостей, расположенных перпендикулярно к фронтальной плоскости проекций π ₂. Поэтому отверстия задают на виде спереди, на котором их форма изображена без искажения. На видах сверху и слева построение проекции отверстий сводится к нахождению линий пересечения отсеков проецирую­щих плоскостей с поверхностью геометрического тела и между собой.

Построение трех проекций правильной шестиугольной призмы с поперечным сквозным окном (рис. 35). Форма и положение сквозного окна относительно граней призмы показаны на рис. 35, а. Грани окна пересекаются со всеми боковыми гранями призмы по двум одинаковым замкнутым ломаным пространственным линиям, состоящим из отрезков прямых (рис. 35, б).

Рис. 35.1

Вначале чертят три проекции целой призмы и фронтальную проекцию окна (рис. 35, в). Призма вместе с окном имеет две вертикальные плоскости симметрии (α || π₂) и β || π ₃), разделяющие ее на четыре равные части. Таким образом, можно рассматривать построение линий пересечения граней окна только с одной частью призмы, например, передней левой (грани I и II на рис. 35, б). На виде спереди концы отрезков этой части линий пересечения обозначены точками А", В", С", D", Е" и F". На виде сверху проекция ломаной линии ABCDEF расположена на горизонтальных проекциях граней I и II. Боковые грани призмы перпендикулярны к плоскости π₁ и проецируются на нее в виде отрезков — сторон шестиугольника. Поэтому для определения положения точек А', В', С', D', Е' и F' достаточно провести через фронтальные проекции этих точек вертикальные линии проекционной связи и продолжить их до пересечения с отрезками I ' и II '.

На виде слева боковая грань I, параллельная плоскости π ₂. про­ецируется в виде вертикального отрезка I". Этой грани принадлежат отрезки линий пересечения — АВ и EF. Их профильные проекции получают с помощью горизонтальных линий проекционной связи. Для построения точек С'" и D"', кроме проведения горизонтальных линий проекционной связи, необходимо отложить на плоскости π₃ расстояние этих точек до плоскости симметрии α. Затем проводят ломаную линию B"C"D'"E'" и строят симметричную ей линию относительно плоскости α.

Грани окна пересекаются между собой по отрезкам фронтально проецирующих прямых, проходящих через точки излома линий пересечения. На горизонтальной и профильной проекциях эти отрезки невидимы, так как находятся внутри призмы, поэтому их изо­бражают штриховыми линиями.

Построение истинной величины наклонного сечения правильной шестиугольной призмы профильно проецирующей плоскостью (рис. 35, г). Заданная плоскость пересекает наружные и внутренние поверх­ности призмы, поэтому фигура сечения состоит из двух контуров.

Рис. 35.2

Истинную величину наклонного сечения определяют с помощью проецирования его на дополнительную плоскость, параллельную секущей плоскости. Фигура сечения имеет ось симметрии, ко­торую проводят параллельно заданной секущей плоскости. Затем приступают к построению наружного контура сечения. На виде слева обозначают места пересечения заданной плоскости с боковыми ребрами призмы — точки 1"', 2'", 3 '", 4'" и с ребрами ее нижнего основания — точки 5'", 6'". Ширину сечения в отмеченных точках определяют по их фронтальным проекциям и переносят на дополнительную плоскость с помощью отрезков 1 " — 2" = 1 — 2, 3" — 4" = 3 — 4 и 5" — 6" = 5 — 6. При этом в обе стороны от оси симметрии контура откладывают половину каждого отрезка.

Для определения фронтальной проекции точек 5 и 6 можно воспользоваться построениями, показанными на рис. 35, г. Они заключаются в том, что при пересечении всех боковых граней призмы фигура сечения имеет две взаимно перпендикулярные оси симметрии.

Построение внутреннего контура сечения (рис. 35, д) выполня­ют в той же последовательности, что и внешнего. Отличие состоит лишь в том, что точки излома контура расположены на внутренней поверхности призмы.

После окончания всех построений на виде слева выполняют профильный разрез, чтобы открыть внутренние формы призмы. Секущая плоскость такого разреза совпадает с профильной плоскостью симметрии β призмы (см. рис. 35, в), поэтому на чертеже ее не обозначают, а разрез не сопровождают надписью. На профильной проекции призмы есть вертикальная ось симметрии, что позволяет разрез со­вместить с видом. На чертеже их разделяет волнистая линия, так как с осью симметрии совпадает изображение внешнего ребра призмы. В последнюю очередь на разрезе и на сечении наносят штриховку.

Построение трех проекций правильной треугольной пирамиды с поперечным окном (рис. 36). По заданной фронтальной проекции пирамиды видно, что окно пересекает все ее боковые грани (рис. 36, а). В результате пересечения граней окна и пирамиды получаются пространственный четырехугольник и плоский треугольник (рис. 36, б).

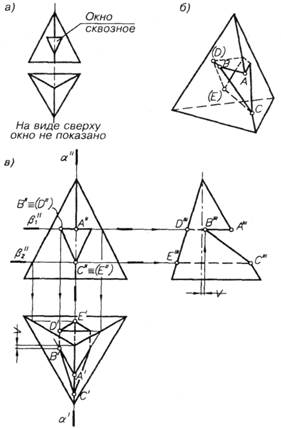
Рис. 36.1

Выполнение чертежа начинают, как обычно, с построения трех проекций целой пирамиды и фронтальной проекции окна (рис. 36, в). Пирамида с окном имеет профильную плоскость симметрии α, поэтому обозначения точек, необходимых для объяснения построений, нанесены лишь на одной левой половине пирамиды.

При определении на виде сверху проекций линий пересечения окна с боковыми гранями пирамиды используют вспомогательные горизонтальные плоскости β₁ и β₂. Их проводят через верхнюю грань окна и его нижнее ребро, которые параллельны плоскости π₁. Плоскости β₁ и β₃ пересекают поверхность пирамиды по треугольникам, подобным ее основанию. Горизонтальные проекции точек А, В, С, D и Е получают на пересечении вертикальных линий связи, проведенных через их фронтальные проекции А", В" ≡ (D ") и С" ≡ (Е") со сторонами построенных треугольников. Затем точки А', В', С' и D', E' соединяют отрезками прямых и строят им симметричные относительно плоскости α.

На виде слева отмеченные точки получают на пересечении горизонтальных линий проекционной связи с передним ребром пирамиды (точки А'", С'") и ее задней гранью, перпендикулярной к плоскости π₃ (точки D'", E '"). При определении положения точки В'" дополнительно откладывают расстояние, указанное на чертеже знаком «V», взятое с плоскости π₁. Затем точки А'" и В'", В'" и С'" соединяют прямыми и получают профильную проекцию линий пересечения окна с передними гранями пирамиды.

В последнюю очередь строят проекции линий пересечения граней окна между собой — отрезков фронтально проецирующих прямых. На видах сверху и слева они невидимы за исключением отрез­ка СЕ, две части которого видны на горизонтальной проекции.

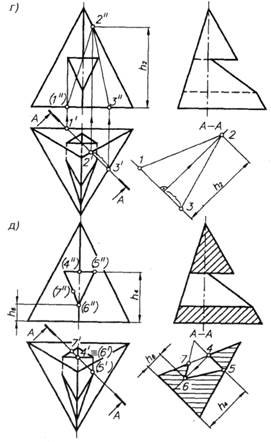
Рис. 36.2

Построение истинной величины наклонного сечения правильной треугольной пирамиды горизонтально проецирующей плоскостью (рис. 36, г). Истинную величину сечения определяют на допол­нительной плоскости, параллельной заданной и смещенной относи­тельно нее на свободное место чертежа (см. рис. 36, г). Заданная плоскость пересекает наружную поверхность пирамиды и грани сквозного окна. Наружный контур сечения имеет форму треугольника 1 — 2 — 3, так как плоскость пересекает основание пирамиды и две ее боковые грани. На дополнительной плоскости вначале строят нижнюю сторону треугольника — отрезок 1 — 3 = 1' — 3'. Затем откладывают от точки 3 расстояние, равное отрезку 2 ' — 3'. Из полученной точки восставляют перпендикуляр к стороне 1 — 3 и откладывают на нем отрезок, равный высоте h₂ точки 2. Построение наружного конту­ра заканчивают проведением сторон треугольника 1 — 2 и 2 — 3.

На внутреннем контуре сечения (см. рис. 36, д) сначала строят с помощью высоты h ₄ линию пересечения заданной плоскости с верхней гранью окна — отрезок 4 — 5 = 4' — 5'. Затем определяют положение точки 6, расположенной под точкой 4 на высоте h ₆. Для построения точки 7 используют дополнительный треугольник, симметричный и равный треугольнику 4 — 5 — 6.

Внутренняя поверхность пирамиды выявлена на виде слева. Се­кущая плоскость совпадает с плоскостью симметрии пирамиды α (см. рис. 36, в), поэтому на чертеже ее положение и профильный разрез не отмечены.

Построение трех проекций прямого кругового цилиндра с поперечным сквозным окном (рис. 37). Плоские отсеки заданного окна, расположенные параллельно и перпендикулярно к оси цилиндра (рис. 37, а), пересекаются с его поверхностью по образующим и дугам (рис. 37, б).

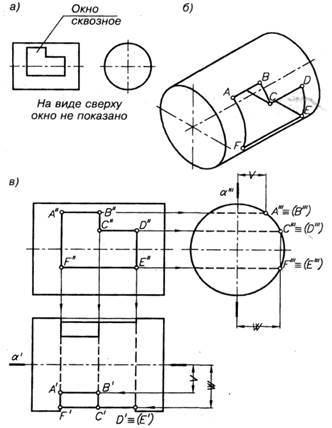
Рис. 37.1

На чертеже строят три проекции цилиндра и фронтальную проекцию окна (рис. 37, в). Данное геометрическое тело имеет фронтальную плоскость симметрии α, поэтому линии пересечения отсеков окна с цилиндрической поверхностью обозначены только на одной ее передней половине. Цилиндрическая поверхность расположена перпендикулярно к плоскости проекций π₃ и проецируется на нее в виде окружности. Обозначенные точки принадлежат той части цилиндрической поверхности, профильной проекцией которой является правая половина окружности. Для построения на виде сле­ва точек А, В, С, D, Е и F через их фронтальные проекции проводят горизонтальные линии проекционной связи, на пересечении кото­рых с правой полуокружностью получают точки А'" ≡ (В'"), С" ≡ (D '") и F" ≡ (E "').

На виде сверху точки А', В', С', D', Е' и F' определяют на пересечении соответствующих вертикальных линий связи и расстояний названных точек от фронтальной плоскости симметрии цилиндра α, указанных на чертеже знаками «V» и «W». Затем строят горизонтальные проекции видимых линий пересечения — отрезки образующих А'В', C'D' и часть образующей E'F', а также проекции дуг, расположенных на верхней половине цилиндра — части дуг A'F' и D'E' дугу В'С'. Далее вычерчивают изображение окна на задней поверхности цилиндра, симметричное относительно плоскости α, и определяют линии пересечения отсеков окна между собой, которые на горизонтальной и профильной проекциях изображают штриховыми линиями.

На чертеже цилиндра его внутренние поверхности выявлены с помощью профильного разреза А — А. Заданный цилиндр не имеет профильной плоскости симметрии, поэтому на чертеже необходимо обозначить секущую плоскость и разрез. На виде слева разрез совмещен с видом, так как профильная проекция цилиндра имеет вертикальную ось симметрии. У заданного цилиндра внутренние поверхности могут быть также выявлены с помощью горизонтального разреза, секущую плоскость которого проводят через ось цилиндра.

Построение истинной величины наклонного сечения прямого кругового цилиндра горизонтально проецирующей плоскостью (рис. 37, г). Истинную величину наклонного сечения получают на дополнительной плоскости, параллельной секущей и расположенной с сохранением с ней линий проекционной связи.

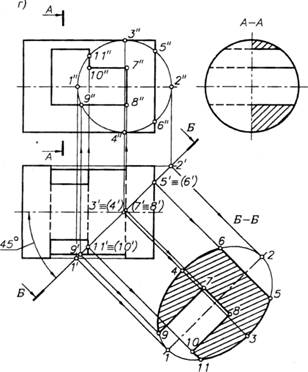
Рис. 37.2

Заданная плоскость, наклоненная к оси цилиндра, пересекает цилиндрическую поверхность по неполному эллипсу и правое основание цилиндра по отрезку прямой. На дополнительной плоскости вначале строят полный эллипс. Его большую ось — отрезок 1 — 2 определяют на виде сверху, продолжив очерковые образующие ци­линдра до пересечения с заданной плоскостью в точках 1' и 2'. Малая ось эллипса — отрезок 3 — 4 — равна диаметру цилиндра. Секущая плоскость составляет с осью цилиндра угол 45°, поэтому на фронтальной проекции эллипс проецируется в виде окружности. Это положение упрощает построение его промежуточных точек на дополнительной плоскости. Их строят по размерам, взятым на виде спереди, например, так определен размер хорды эллипса 5 — 6 = 5" — 6".

Построение внутреннего контура сечения начинают с обозначения на виде сверху точек, определяющих линии пересечения заданной плоскости с гранями окна — точки 9', 11' ≡ (10') и (7' ≡ 8'). За­тем через эти точки проводят вертикальные линии проекционной связи и находят их фронтальные проекции. Далее через эти же точ­ки проводят линии связи, перпендикулярные плоскости сечения. На линии проекционной связи, проведенной через точки (7' ≡ 8'), откладывают в обе стороны от большой оси эллипса половину отрезка 7" — 8" и получают точки 7 и 8. Через точки 7 и 8 проводят прямые, параллельные оси 1 — 2, и продолжают их до пересечения с внешним контуром в точке 9 и линией проекционной связи, проведенной через точку 11' ≡ (10') в точке 10. На этой же линии при пересечении ее с контуром эллипса отмечают точку 11.

При точном определении истинной величины фигуры сечения должно быть получено равенство отрезков: 8 — 9 = 8' — 9' и 10 — 11 = 10" — 11'.

Построение наклонного сечения заканчивают его обводкой, на­несением штриховки и обозначением секущей плоскости.

Построение трех проекций прямого кругового конуса с попе­речным сквозным окном (рис. 38). Сквозное окно ограничено боковыми отсеками, плоскости которых проходят через вершину конуса, и горизонтальными отсеками, расположенными перпендикулярно к его оси (рис. 38, а). Поэтому линиями пересечения этих плоских отсеков с конической поверхностью являются образующие и дуги окружностей (рис. 38, б).

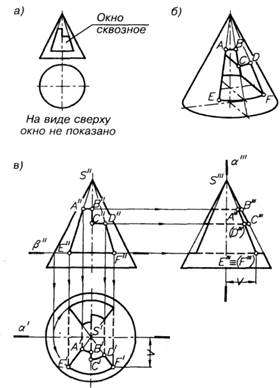
Рис. 38.1

На чертеже строят три проекции конуса и фронтальную проекцию окна (рис. 38, в). Конус с окном имеет фронтальную плоскость симметрии α, что позволяет обозначить линии пересечения отсеков окна с конической поверхностью лишь на передней половине конуса.

Для построения на виде сверху отмеченных линий пересечения через нижний отсек окна проводят вспомогательную горизонтальную плоскость β. Эта плоскость пересекает коническую поверхность по окружности, частью которой является дуга EF. Точки Е' и F' получают на пересечении вертикальных линий проекционной связи, проведенных через их фронтальные проекции (точки Е", F"), со вспомогательной окружностью. Затем соединяют прямыми точки E' и S', F' и S' и на построенных образующих конуса с помощью вертикальных линий связи получают точки А' и D'. Горизонтальную проекцию дуги А В проводят радиусом, равным отрезку S'A', aдуги CD — радиусом, равным отрезку S'D'.

На профильной проекции вначале определяют положение обра­зующих SE и SF. Точку Е'" = (F'") получают на пересечении горизонтальной линии проекционной связи, проведенной через нижний отсек окна, и расстояния, отмеченного на чертеже знаком «V». Для построения на виде слева точек А, В, С и D через верхние отсеки окна проводят горизонтальные линии связи и продолжают их до пе­ресечения с правой очерковой образующей конуса (точки В'", С'") и образующими S"'E'" (точка А'") и S"'(F"') (точка (D '").

Далее на видах сверху и слева строят проекции линий пересечения, симметричные полученным относительно фронтальной плоскости симметрии α. Отсеки плоскостей, ограничивающих окно, пересекаются между собой по отрезкам фронтально проецирующих прямых. На виде сверху эти отрезки невидимы, а на виде слева у отрезка, проходящего через точку С'", видны небольшие участки, выступающие за образующую А'"Е'" и симметричную ей относительно плоскости α.

Построение истинной величины сечения прямого кругового ко­нуса фронтальной плоскостью (рис. 38, г). Заданная секущая плоскость параллельна плоскости π₂, поэтому на фронтальной проекции фигура сечения не искажена и ее изображение на дополнительной плоскости полностью повторяет проекцию сечения на виде спереди.

Рис. 38.2

Секущая плоскость, параллельная оси конуса, пересекает коническую поверхность по гиперболе. Ее вершина на виде сверху расположена в середине горизонтальной проекции сечения — отрезка 1' — 2' и совпадает с точкой В'. Вначале на виде спереди строят проекцию нижней хорды гиперболы — отрезок 1" — 2", который является линией пересечения заданной плоскости с основанием конуса. Промежуточные точки гиперболы получают с помощью вспо­могательных окружностей, проведенных на конической поверхности. Для примера на рис. 38, г проведена окружность на высоте h и показано построение двух промежуточных точек гиперболы.

На дополнительной плоскости сначала чертят наружный контур сечения по размерам, взятым с его фронтальной проекции. Отрезок 1 — 2 = 1 " — 2' проводят параллельно секущей плоскости на свободном месте чертежа. Из середины отрезка 1 — 2 восставляют к нему перпендикуляр, отложив на котором высоту гиперболы, полу­чают точку В. Затем строят 10—12 промежуточных точек гипербо­лы и соединяют их плавной линией.

Вычерчивание внутреннего контура (рис. 38, д) начинают с изо­бражения линии пересечения заданной плоскости с нижним отсеком окна — отрезка 3 — 4 = 3" — 4", расположенного на высоте h₃. Через точку В проводят прямую, параллельную отрезку 3 — 4, и на ней в обе стороны от точки В откладывают ширину верхнего отсека окна. Концы построенного отрезка соединяют прямыми с точками 3 и 4 и получают линии пересечения заданной плоскости с боковыми гранями окна. На пересечении прямой, проведенной через точку 3, и гиперболы получают точку 5, а точку 6 определяют отложив на другой прямой высоту h₆. Затем строят линии пересечения заданной плоскости со средним горизонтальным отсеком окна — отрезок 6 — 7=6" — 7" и с его вертикальной гранью — отрезок В— 7= В" — 7".

Перед обводкой проекций конуса на виде слева выполняют профильный разрез А — А. Заданный конус с окном не имеет профильной плоскости симметрии, поэтому на чертеже необходимо отметить положение секущей плоскости и сопроводить разрез надписью. В последнюю очередь на разрезе и на сечении наносят штриховку.

Построение трех проекций геометрического тела с поперечным сквозным окном (рис. 39). Верхняя часть геометрического тела представляет собой правильную треугольную пирамиду, а нижняя — прямой круговой цилиндр (рис. 39, а). Сквозное окно пересекает поверхность обеих частей геометрического тела (рис. 39, б).

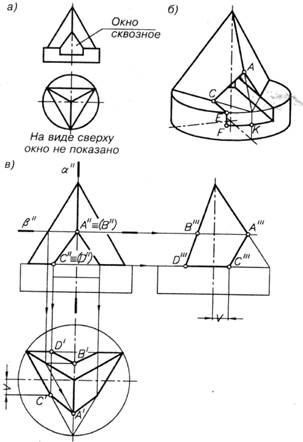
Рис. 39.1

Проекции геометрических тел с поперечным сквозным окном, составленные как бы из двух частей, можно вычерчивать в разной последовательности. В одном случае полностью строят горизонтальную, затем профильную проекции всего геометрического тела с окном, а в другом — определяют на видах сверху и слева проекции окна на одной его части, затем на другой. В данном примере при­нят вариант раздельного построения каждой части геометрического тела и окна.

На чертеже после построения трех проекций геометрического тела и фронтальной проекции сквозного окна приступают к определению линий пересечения верхней части окна с поверхностью пирамиды (рис. 39, в). Геометрическое тело с окном имеет профильную плоскость симметрии α, поэтому на чертеже обозначена одна половина искомых линий пересечения.

Для построения на виде сверху точек А и В используют вспомо­гательную горизонтальную плоскость β, проведенную через их фронтальные проекции — точку А" ≡ (В'"). Точки А' и В' определя­ют на пересечении вертикальной линии проекционной связи и сторон треугольника, полученного при сечении пирамиды плоскостью β. Точки С' и D' получают на пересечении горизонтальных проекций ребер основания пирамиды, которым они принадлежат, с вертикальной линией проекционной связи, проведенной через точку С" ≡ (D"). Затем точки А' и С', В' и D' соединяют прямыми и чертят симметричные им относительно плоскости α.

На виде слева профильные проекции точек А, В, D определяют с помощью горизонтальных линий проекционной связи, проведенных через их фронтальные проекции и продолженных до пересечения с передним боковым ребром пирамиды (точка А'") и ее задней гранью (точки В"', D '"). Точку С'" получают на пересечении горизонтальной линии связи и расстояния, отмеченного знаком «V» и перенесенного на плоскость π₃ с плоскости π₁.

Горизонтальные и вертикальные отсеки нижней части окна, расположенные параллельно и перпендикулярно к оси цилиндра, пересекают цилиндрическую поверхность по ее образующим и дугам (см. рис. 39, б). Эти линии одинаковы на передней, задней, правой и левой частях цилиндрической поверхности, поэтому на чертеже обозначена лишь их четвертая часть — образующая EF и дуга FK (рис. 39, г).

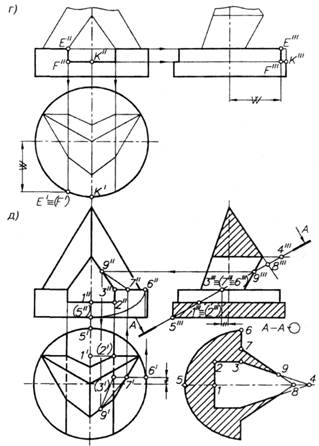
Рис. 39.2

На виде сверху отмеченные линии расположены на полуокружности — горизонтальной проекции передней половины цилиндрической поверхности. Проекции образующей — точку Е' = (F¹) и дуги — дугу (F')K' получают с помощью вертикальных линий связи. Для построения на виде слева точек Е, F, К через их фронтальные проекции проводят горизонтальные линии проекционной связи и продолжают их до пересечения с расстоянием, отмеченным знаком «W» (точки Е'", F"') и с очерковой образующей цилиндра (точка К"'). Затем на плоскости π₃ строят линии, симметричные построенным относительно оси цилиндра.

Построение проекций заканчивают изображением линий пересечения отеков окна между собой и с верхним основанием цилиндра (рис. 39, д). На виде сверху четыре участка последних линий видимы. Затем выполняют профильный разрез, плоскость которо­го совпадает с плоскостью симметрии α геометрического тела (см. рис. 39, в).

Построение истинной величины сечения геометрического тела профильно проецирующей плоскостью (см. рис. 39, д). По положению на профильной проекции заданной плоскости определя­ют, что она пересекает обе части геометрического тела и сквозное окно. На этой же проекции отмечают точки, необходимые для вычерчивания контура сечения. Затем находят их горизонтальные и фронтальные проекции. Сечение имеет ось симметрии. На чертеже точки его контура обозначены с одной стороны этой оси, поэтому вначале определяют половину истинной величины сечения, а потом строят симметричную ей относительно оси контура.

В рассматриваемом примере дополнительная плоскость смеще­на относительно секущей плоскости и повернута до горизонтально­го положения оси симметрии сечения. Определение его истинной величины начинают с вычерчивания линий пересечения заданной плоскости с правой половиной нижней части окна — отрезков 1 — 2 = 1" — 2" и 2 — 3 = 2 '" — 3'". Для построения линии пересе­чения правой наклонной грани окна с заданной плоскостью на виде слева продолжают его верхнее ребро и находят точку 4'". Затем на дополнительной плоскости откладывают отрезок 1 — 4 = 1'" — 4'" и соединяют прямой линией точки 3 и 4. У наружного контура се­чения вначале строят линию, полученную при пересечении задан­ной плоскости с правой частью цилиндрической поверхности — участок эллипса. На оси сечения откладывают отрезок 1 — 5= 1'" — 5'", а на перпендикуляре к оси, проведенном через точку 3, отрезок 3 — 6 = 3' — 6 '. Промежуточные точки эллипса строят, отмечая положение его хорды на виде слева, а затем определяя ее величину на виде сверху. Отрезок 6 — 7 = 6' — 7 является линией пересечения секущей плоскости с верхним основанием цилиндра. Для определения линии пересечения с правой передней боковой гранью пирамиды на виде слева продолжают ее переднее ребро и находят точку 8'". На оси симметрии откладывают отрезок 1 — 8= 1" — 8'" и соединяют прямой точки 7 и 8. На пересечении отрезков 3 — 4 и 7 — 8 получают точку 9.

Далее вычерчивают другую половину контура сечения, симметричную относительно его оси, обводят контур и наносят штриховку.

Дата добавления: 2015-07-13