Группы геометрических тел

Группы геометрических тел могут состоять из сочетаний двух и более геометрических фигур или их частей. При этом геометрические тела, образующие группу, либо расположены порознь, либо соприкасаются друг с другом.

Ниже рассматриваются группы второго типа, состоящие из трех геометрических тел, таких как прямые призмы и пирамиды, цилиндры и конуса, шары. Описания построения проекций и сечений проецирующими плоскостями перечисленных фигур имеются в предыдущих разделах. Их используют при выполнении проекций и на­клонных сечений геометрических тел, объединенных в одну группу.

Порядок вычерчивания проекций группы геометрических тел может быть разным. В одном случае полностью строят изображения всех тел, образующих группу, на виде спереди, затем на виде сверху и на виде слева, а в другом — последовательно строят три проекции каждого геометрического тела. Раздельное построение проекций геометрических тел предпочтительнее, так как при этом один и тот же размер, определяющий их форму, откладывают сразу на всех проекциях, что ускоряет и упрощает выполнение чертежа.

Построение трех проекций и истинных величин фигур при сечении заданной группы геометрических тел произвольной профильно проецирующей плоскостью (рис. 21, а). По заданным про­екциям группы геометрических тел можно судить, что ее основанием служит правильная шестиугольная призма, на которую поставле­ны полуконус и примыкающая к нему четверть шара.

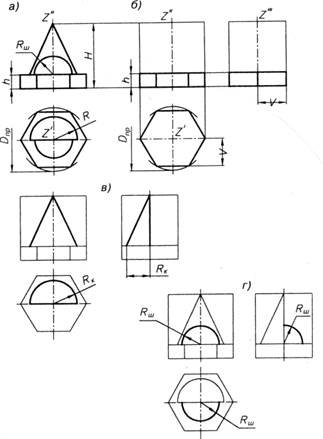
Рис. 21

Работу над чертежом, согласно приведенным ранее рекомендаци­ям, начинают с определения габаритных размеров группы на всех видах и положения ее вертикальной оси. Далее последовательно строят три проекции шестиугольной призмы (рис. 21, б) полу конуса (рис. 21, в) и четверти шара (рис. 21, г). На рис. 21, в, г контуром выделены только те линии, которые дополняют предыдущий чертеж.

После окончания всех построений на виде слева задают секущую профильно проецирующую плоскость α (рис. 22). Положение плос­кости α выбрано таким, что она пересекает все три геометрические тела и равнонаклонена к плоскостям проекций π₂ и π₁. В результате пересечения данных геометрических тел с плоскостью α получаются три соприкасающиеся фигуры, имеющие общую ось симметрии. Раздельное построение проекций и истинных величин этих фигур показано на рис. 23.

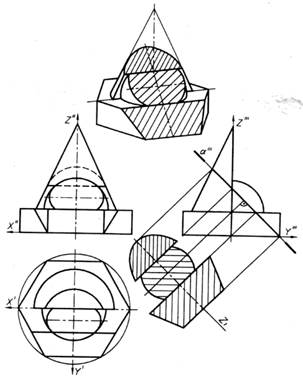
Рис. 22

Плоскость α наклонена к оси вращения конуса так, что пересе­кает коническую поверхность по эллипсу (рис. 23, а), а полуконус — по его части, меньшей половины эллипса. Проекции фигуры сечения строят по точке А — концу большой оси эллипса, замыкающей хорде ВС и промежуточным точкам эллипса, количество кото­рых должно быть достаточным для того, чтобы получить плавную кривую. На видах спереди и сверху фигура сечения проецируется в виде части эллипса с одинаковым искажением, но изображается соответственно невидимыми и видимыми линиями.

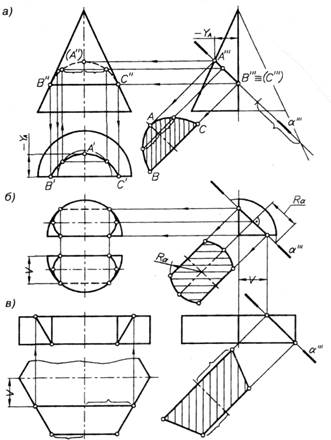
Рис. 23

Истинную величину фигуры сечения получают на дополнитель­ной плоскости, параллельной плоскости α, откладывая от ее оси симметрии полухорды эллипса, взятые с его фронтальной проекции.

Профильно проецирующая плоскость α пересекает поверхность шара по дуге окружности радиуса R _α(рис. 23, б). Для определения его размера из центра шара опускают перпендикуляр на плоскость α и продолжают очерк шара до пересечения с ее профильной проекцией. Фигура сечения представляет собой часть круга, ограниченную с двух сторон его диаметра одинаковыми хордами. Дуги окружности радиуса R _αпроецируются на фронтальной и горизон­тальной проекциях в виде одинаковых частей эллипса. Истинную величину фигуры сечения определяют на дополнительной плоско­сти с помощью линий проекционной связи и дуг радиуса R _α.

Шестиугольную призму плоскость α пересекает по переднему ребру ее нижнего основания, примыкающим к нему боковым гра­ням и верхнему основанию (рис. 23, в). Фигура сечения представля­ет собой равнобочную трапецию. Определение ее проекций и истинной величины подробно показано на рис. 23, в.

Штриховку фигур сечения выполняют по правилам, изложенным в ГОСТ 2.306—68, выбирая такое направление штриховки для каждой фигуры, чтобы избежать совпадения ее линий с линиями контура или осью симметрии. Кроме того, интервалы между линия­ми штриховки задаются разными.

Дата добавления: 2015-07-13