Конуса усеченные

При сечении прямого кругового конуса плоскостью простейшими фигурами являются: равнобедренный треугольник, если плоскость проходит через вершину конуса (рис. 13, а) или его, ось, и круг, когда плоскость перпендикулярна к оси конуса (рис. 13, б). При всех других положениях плоскости относительно оси конуса она пересекает коническую поверхность по лекальной кривой.

Секущая плоскость, параллельная двум образующим конуса, например SA и SB, пересекает коническую поверхность по гиперболе. При этом секущая плоскость может быть наклоненной к оси конуса (рис. 14, а) или быть параллельной ей (рис. 14, б). Характерным признаком таких секущих плоскостей является то, что они пересекают обе полости конической поверхности.

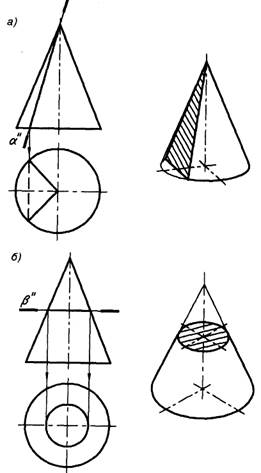
Рис. 13

Плоскость, параллельная одной из образующих конуса, например SC, пересекает коническую поверхность по параболе (рис. 14, в). Секущая плоскость, параллельная одной образующей конуса, пересекает только одну полость конической по­верхности, поэтому парабола, в отличие от гиперболы, имеет одну ветвь.

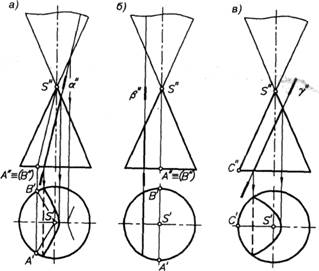
Рис. 14

В случае, когда секущая плоскость наклонена к оси конуса так, что пересекает все его образующие, фигурой сечения является эллипс с большой осью АВ и малой CD (рис. 15, а). Если же плоскость пересекает все образующие конической поверхности при про­должении ее за пределами конуса, то фигура сечения представляет собой неполный эллипс (рис. 15, б).

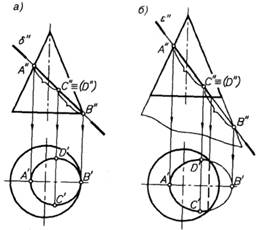
Рис. 15

Построение трех проекций контура сечения и его истинной величины при пересечении конуса горизонтально проецирующей плоскостью α(рис. 16). Плоскость α и ось вращения конуса перпендикулярны к плоскости π₁ (рис. 16, а), следовательно, они параллельны между собой и заданная плоскость α пересекает коническую поверхность по гиперболе. Фигура сечения представляет собой часть плоскости, ограниченной гиперболой и замыкающей ее хордой (рис. 16, б).

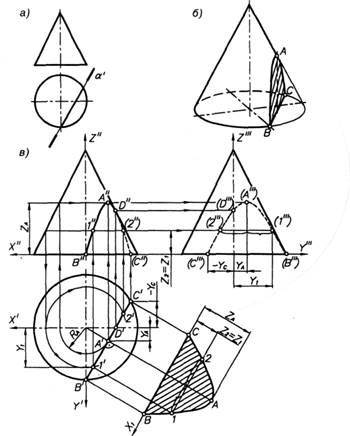
Рис. 16

На чертеже строят три проекции конуса и горизонтальную про­екцию заданного сечения (рис. 16, в). На виде сверху определяют положение вершины гиперболы — точки А', которая находится в середине горизонтальной проекции фигуры сечения. Фронтальную А" и профильную А'" проекции вершины получают с помощью дуги радиуса R_A, линий проекционной связи и координаты Y_A. Плоскость α пересекает основание конуса по хорде ВС. Проекции точки В отмечают без дополнительных линий. Для построения точки С на виде спереди проводят вертикальную линию проекционной связи, а на виде слева ее получают, отложив координату YC. Затем находят точку D'', расположенную на очерковой образующей фронтальной проекции конуса и определяющую границу видимости гиперболы на виде спереди.

Остальные точки гиперболы, лежащие между ее вершиной А и хордой ВС, являются промежуточными. Гипербола имеет ось симметрии, от которой промежуточные точки одного уровня удалены на одинаковое расстояние, что позволяет уменьшить количество вспомогательных линий при определении их проекций. В качестве вспомогательных линий используют образующие конуса или окружности, проведенные на его поверхности. Для примера на рис. 16, в показано построение проекций промежуточных точек 1 и 2.

Построенная гипербола расположена на той части конической поверхности, которая невидима на виде слева. Поэтому при обвод­ке чертежа профильную проекцию кривой изображают штриховы­ми линиями.

Истинную величину фигуры сечения получают на дополнительной плоскости, параллельной плоскости α. Новая ось проекций х₁ совмещена с хордой ВС, принадлежащей плоскости π₁, и от нее замеряют координаты z точек гиперболы.

Построение трех проекций контура сечения и его истинной величины при пересечении фронтально проецирующей плоскостью α прямого кругового конуса (рис. 17). По заданной фронтальной проекции плоскости α (рис. 17, а) видно, что она наклонена к оси вращения конуса так, что пересекает все его образующие, т. е. фигурой сечения является эллипс (рис. 17, б).

Построив три проекции конуса и фронтальную проекцию заданного сечения, обозначают на ней концы осей эллипса (рис. 17, в): большой — точки А", В" и малой — точки С", D". Эллипс имеет две оси симметрии, поэтому точка С" ≡ (D'') расположена в середине отрезка А"В". На видах сверху и слева точки А и В получают с по­мощью линий проекционной связи. Горизонтальные проекции точек С и D отмечают на вспомогательной окружности, проведенной через них на поверхности конуса, а на виде слева точки С" и D"' получают, отложив их расстояние от плоскости симметрии конуса β. Далее находят профильные проекции точек Е и F, расположен­ные на очерковых образующих конуса и определяющие границу ви­димости эллипса на виде слева. В последнюю очередь строят 10—12 промежуточных точек эллипса. Определение их проекций аналогично построению проекций точек С и D. При обводке черте­жа невидимую часть проекции эллипса на виде слева изображают штриховыми линиями.

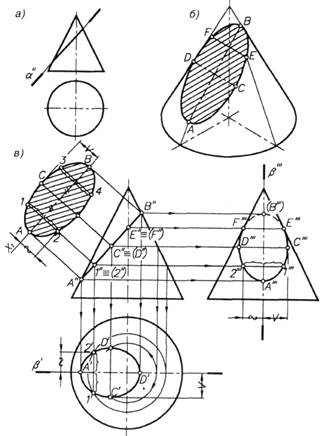
Рис. 17

Истинную величину эллипса, искаженного на плоскостях π₁, π₂, π₃, определяют на дополнительной плоскости, параллельной секу­щей плоскости α. Новую ось х₁ совмещают с большой осью АВ эл­липса, параллельной плоскости π₂, и от нее откладывают отрезки, равные полухордам эллипса, замеряя их на горизонтальной проекции. Эллипс, как уже отмечалось, имеет две оси симметрии, поэто­му, зная положение одной промежуточной точки, например 1, можно построить еще три точки эллипса, симметричные ей относитель­но этих осей, например точки 3, 4 и 5.

Построение по заданной фронтальной проекции усеченного прямого кругового конуса его горизонтальной и профильной про­екций (рис. 18). Заданные секущие плоскости перпендикулярны к плоскости π ₂ (рис. 18, а), поэтому по фронтальной проекции усе­ченного конуса можно судить о том, по каким линиям пересекает каждая плоскость коническую поверхность (рис. 18, б). Фронтально проецирующая плоскость α проходит через вершину конуса и пересекает его по двум образующим. Горизонтальная плоскость β, пер­пендикулярная к оси вращения конуса, пересекает его поверхность по окружности. Еще одна плоскость — фронтально проецирующая плоскость γ — параллельна очерковой образующей конуса, т. е. в сечении получается парабола.

Решение примера выполняют в обычном порядке: строят три проекции целого конуса и фронтальную проекцию заданного выре­за (рис. 18, в). Усеченный конус имеет фронтальную плоскость симметрии δ, поэтому точки фигур сечения, необходимые для по­строения их проекций, обозначены только на передней поверхности конуса. На чертеже проекции этих точек получают с помощью та­ких же вспомогательных линий и приемов, которые были разобра­ны в предыдущих примерах (см. рис. 16 и 17). Поэтому ниже изло­жена лишь последовательность определения на видах сверху и сле­ва проекций обозначенных точек.

Вначале определяют положение образующих конуса, получен­ных при пересечении его с плоскостью α (образующая SA и сим­метричная ей). Затем изображают горизонтальную и профильную проекции окружности, расположенной в плоскости β, и проекции точек В и D лежащих на ней и симметричных им. Построение па­раболы начинают с определения проекций ее вершины — точки С и точки Е, принадлежащей очерковой образующей конуса на виде слева. Далее определяют положение проекций ее промежуточных точек, например точки 1 и симметричной ей.

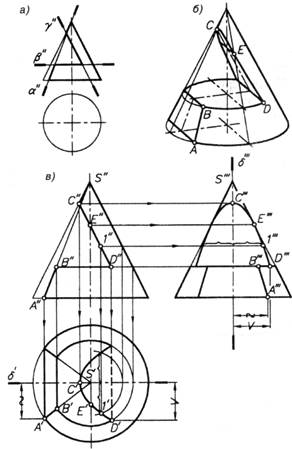
Рис. 18

Чертеж заканчивают изображением линий пересечения плоскости β с плоскостями α и γ — отрезков фронтально проецирующих прямых, проходящих через точки В и D. На построенных проекциях усеченного конуса штриховыми линиями показывают невидимые части параболы.

Дата добавления: 2015-07-13