Призмы усеченные

Многогранники

Многогранником называют геометрическое тело, ограниченное со всех сторон плоскими многоугольниками. Наиболее распростра­ненными видами многогранников являются прямые призмы и пира­миды. Элементы их поверхности обозначены на рис. 4 на примере призмы.

Рис. 4

При сечении многогранников плоскостями получают плоские многоугольники, число сторон которых равно чис­лу пересеченных граней. Стороны и вершины этих многоугольни­ков представляют собой линии и точки пересечения граней и ребер многогранников с секущими плоскостями. Таким образом, решение задач на построение сечений многогранников плоскостями сводится к определению линии пересечения двух плоскостей и точки пересе­чения прямой с плоскостью.

Форма многоугольника, полученного при сечении призмы плоскостью, зависит от ее положения относительно основания призмы. Секущая плоскость может быть параллельна, перпендикулярна или наклонена к основанию призмы. Соответственно фигурами сечения будут: многоугольник, равный основанию призмы или его части; прямоугольник (в частном случае квад­рат); многоугольник, повторяющий форму основания призмы или его части, но растянутую в продольном или поперечном на­правлениях.

Построение трех проекций контура сечения и его истинной величины при пересечении фронтально проецирующей плоско­стью α прямой треугольной призмы (рис. 5). По заданной фронтальной проекции плоскости α (рис. 5, а) видно, что она наклонена к основаниям призмы и пересекает все ее боковые грани и верхнее основание, т. е. фигура сечения представляет собой четырехуголь­ник (рис. 5, б).

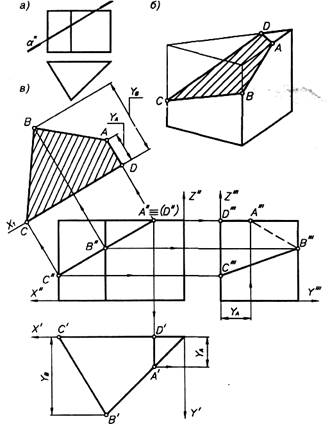
Рис. 5

Решение примера начинают с вычерчивания двух заданных проекций призмы и построения ее вида слева (рис. 5, в). Затем на виде спереди изображают проекцию фигуры сечения и обознача­ют ее вершины— А", В", С" и D" — точки пересечения плоско­сти α с ребрами призмы. Для построения их горизонтальных и профильных проекций достаточно провести соответствующие ли­нии проекционной связи, так как грани призмы и плоскость α занимают частные положения. Дополнительную линию проводят лишь при построении профильной проекции точки А для перено­са координаты Y_A с плоскости π₁ на плоскость π ₃. Далее на черте­же строят линии пересечения граней призмы с плоскостью α, т. е. проекции сторон четырехугольника ABCD, и отмечают видимость тех его сторон, изображения которых не совпадают с про­екциями граней призмы.

Фигура сечения изображена на основных плоскостях проекций π ₁ π ₂, π₃ с искажением. Ее истинную величину получают проециро­ванием на дополнительную плоскость, параллельную плоскости α, выполняя одну замену плоскостей проекций. Новую ось проекций х₁ совмещают со стороной CD, параллельной плоскости α, и от нее замеряют координаты у для точек А и В.

Построение по заданной фронтальной проекции правильной усеченной четырехугольной призмы ее горизонтальной и про­фильной проекций (рис. 6). Заданный вырез образован четырьмя плоскостями, перпендикулярными плоскости π₂ (рис. 6, а): горизонтальной α, двумя профильными β₁ и β₂ и фронтально проецирую­щей γ. Эти плоскости пересекаются с гранями призмы и между со­бой. Поэтому форма и размер фигур сечения зависят не только от положения названных плоскостей относительно оснований призмы, но и относительно друг друга (рис. 6, б).

Рис. 6

Выполнение чертежа начинают с построения трех проекций це­лой призмы и фронтальной проекции заданного выреза (рис. 6, в). Усеченная призма симметрична относительно фронтальной плоско­сти δ, что позволяет обозначить вершины фигур выреза, принадле­жащие лишь передним граням призмы. Плоскости α, β₁, β₂ и γ пе­ресекаются с этими гранями соответственно по отрезкам АВ, ВС, EF, CD и DE. На виде сверху проекции упомянутых отрезков рас­положены на проекциях боковых граней призмы, занимающих го­ризонтально проецирующее положение. Для построения профиль­ных проекций точек А и D, принадлежащих боковым ребрам приз­мы, достаточно провести горизонтальные линии проекционной свя­зи, а для точек В, С и Е, F необходимо еще отложить их расстояния до плоскости симметрии δ. Полученные точки А'", В'", С"', D '", Е'", F"' последовательно соединяют отрезками прямых и строят от­резки, симметричные им относительно плоскости δ. Чертеж закан­чивают изображением на видах сверху и слева линий пересечения заданных секущих плоскостей между собой и с верхним основани­ем призмы, т. е. отрезков фронтально проецирующих прямых, про­ходящих через точки В, С и Е, F.

Построение горизонтальной и профильной проекций усеченной призмы можно выполнять и в ином порядке, например, последова­тельно строить на плоскостях проекций π₁ и π₃ изображения каж­дой фигуры выреза, полученной при сечении призмы плоскостями: α (треугольник), β₁ и β₂ (прямоугольники) и γ (неправильный шес­тиугольник).

Дата добавления: 2015-07-13