Шары усеченные

Фигурой сечения шара плоскостью является круг. Диаметр окружности сечения зависит от расстояния секущей плоскости до центра шара. Плоскость, проходящая через его центр, пересекает поверхность шара по окружности, диаметр которой равен диаметру шара. По мере удаления секущей плоскости от центра шара диаметр окружности, получающейся в сечении, уменьшает­ся (рис. 19, а).

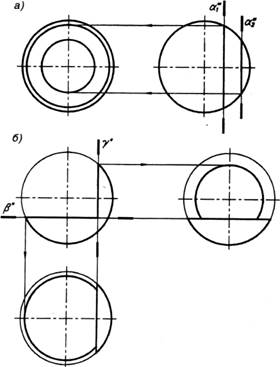
Рис. 19

Форма проекции окружности, расположенной на поверхности шара, зависит только от ее положения относительно плоскостей проекций. Такая окружность может быть параллельна, перпендику­лярна или наклонена к плоскости проекций и соответственно будет проецироваться: в истинную величину; в виде отрезка, равного ее диаметру; эллипса. Если заданные плоскости пересекаются между собой, то фигуры сечения представляют собой неполные круги (рис. 19, б).

Построение по заданной фронтальной проекции усеченного шара его горизонтальной и профильной проекций (рис. 20). Вырез на шаре образован тремя плоскостями α, β, γ перпендикулярными к плоскости проекций π ₂ (рис. 20, а) и пересекающимися между собой таким образом, что в сечениях получаются неполные круги (рис. 20, б).

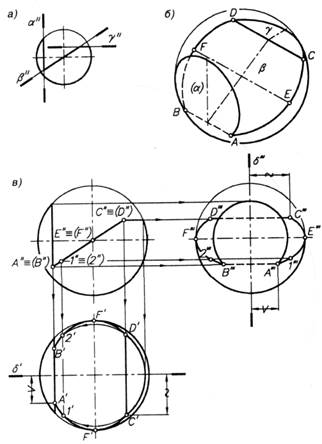
Рис. 20

На чертеже строят три проекции целого шара и фронтальную проекцию заданного выреза (рис. 20, в). Плоскости α и γ являются плоскостями уровня (α || π ₃, γ || π₁), поэтому части кругов, получающиеся при сечении ими шара, проецируются в истинную величину соответственно на видах слева и сверху. Профильная плоскость α пересекает поверхность шара по дуге окружности радиуса R _α, а горизонтальная γ — по дуге радиуса R_γ. Профильные и горизонталь­ные проекции этих дуг и ограничивающих их хорд АВ и CD получают с помощью линий проекционной связи и расстояний точек А, В и С, D до плоскости симметрии шара δ.

Фронтально проецирующая плоскость β наклонена к плоскостям проекций π₁ и π ₃, в результате чего фигура сечения — часть круга — проецируется на них с искажением в виде неполного эллипса. Его большая ось EF равна диаметру шара, так как плос­кость β проходит через его центр. Промежуточные точки на видах сверху и слева, например точки 1 и 2, определяются с помощью вспомогательных окружностей, проведенных через них на поверхности шара.

Чертеж заканчивают обводкой видимых и невидимых линий на построенных проекциях усеченного шара.

Дата добавления: 2015-07-13