Особые случаи в применении критерия

АЛГОРИТМ 13

Гипотезы

Н₀: Распределение взглядов Агафьи Тихоновны между женихами не отличается от равномерного распределения.

Н₁: Распределение взглядов Агафьи Тихоновны между женихами отли­чается от равномерного распределения.

Теперь нам нужно определить теоретическую частоту взгляда при равномерном распределении. Если бы все взгляды невесты распределя­лась равномерно между 4-мя женихами, то, по-видимому, каждый из них получил бы по ¹/₄ всех ее взглядов.

Переведем эти рассуждения на более формализованный язык. Теоретическая частота при сопоставлении эмпирического распределения с равномерным определяется по формуле:

где п - количество наблюдений;

к - количество разрядов признака.

В нашем случае признак - взгляд невесты, направленный на ко­го-либо из женихов; количество разрядов признака - 4 направления взгляда, по количеству женихов; количество наблюдений - 32.

Итак, в нашем случае:

Теперь мы будем сравнивать с этой теоретической частотой все эмпирические частоты.

На Рис. 4.6 сопоставления эмпирических частот с теоретической представлены графически. Похоже, что области расхождений достаточ­но значительны, и Никанор Иванович явно опережает других женихов. Иван Павлович еще может на что-то надеяться, но для Ивана Кузьми­ча и Балтазара Балтазарыча отставка, по-видимому, неизбежна.

Однако для того, чтобы доказать неравномерность полученного эмпирического распределения, нам необходимо произвести точные рас­четы. В методе χ²они производятся с точностью до сотых, а иногда и до тысячных долей единицы.

Расчеты будем производить в таблице по алгоритму.

Расчет критерия χ2

Занести в таблицу наименования разрядов и соответствующие им эмпирические частоты (первый столбец).

Рядом с каждой эмпирической частотой записать теоретическую частоту (второй столбец).

Подсчитать разности между эмпирической и теоретической частотой по каждому разряду (строке) и записать их в третий столбец.

4. Определить число степеней свободы по формуле:

ν=κ-1

где κ - количество разрядов признака.

Если ν = 1, внести поправку на "непрерывность".

5. Возвести в квадрат полученные разности и занести их в четвертый столбец.

6. Разделить полученные квадраты разностей на теоретическую частоту и записать результаты в пятый столбец.

7. Просуммировать значения пятого столбца. Полученную сумму обозначить как χ²_ЭМП.

8. Определить по Табл. IX Приложения 1 критические значения для данного числа степеней свободы V.

Если χ²_эмп меньше критического значения, расхождения между распределениями статистически недостоверны.

Если χ²_эмп равно критическому значению или превышает его, расхождения между распределениями статистически достоверны.

Все вычисления для данного случая отражены в Табл. 4.2.

Таблица 4.2

Расчет критерия χ2 при сопоставлении эмпирического распределения взгляда Агафьи Тихоновны между женихами с равномерным распределением

Разряды - женихи	Эмпирическая частота взгляда (fэj)	Теоретическая частота (fт)	(fэj-fт)	(fэj-fт)^2	(fэj-fт)^2/ fт
	Никанор Иванович Иван Кузьмич Иван Павлович Балтазар Балтазарыч			+6   -3     -3		4.500   1.125     1.125
Суммы					6.750

Может показаться, что удобнее суммировать все возведенные в квадрат разности между эмпирическими и теоретическими частотами, а затем уже эту сумму разделить на f _т. В данном случае это возможно, так как f _т для всех разрядов одинакова. Однако позже мы увидим, что так бывает далеко не всегда. Нужно быть внимательными или, экономя свое внимание, просто взять за правило всякий раз вычислять (f _{э i} — f _т)²/ f _т до суммирования.

Необходимо также всякий раз убеждаться в том, что сумма раз­ностей между эмпирическими и теоретической частотами (сумма по третьему столбцу) равна 0. Если это равенство не соблюдается, это означает, что в подсчете частот или разностей допущена ошибка. Необ­ходимо найти и устранить ее прежде чем переходить к дальнейшим расчетам.

Алгоритм вычислений, таким образом, выражается формулой:

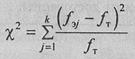
где f_эj - эмпирическая частота по j-тому разряду признака; f _т - теоретическая частота; j - порядковый номер разряда; k - количество разрядов признака. В данном случае:

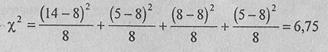
Для того, чтобы установить критические значения %, нам нужно определить число степеней свободы V по формуле: ν= k -l

где k - количество разрядов. В нашем случае ν=4—1=3. По Табл. IX Приложения 1 определяем:

Построим "ось значимости". Ясно, что чем больше отклонения эмпирических частот от теоретической, тем больше будет величина χ2. Поэтому зона значимости располагается справа, а зона незначимости -слева.

К сожалению, на основании этих данных тетушка не сможет дать Агафье Тихоновне обоснованного ответа:

χ² _эмп<χ² _кр.

Ответ: Н₀ принимается. Распределение взгляда Агафьи Тихо­новны между женихами не отличается от равномерного распределения.

Но, допустим, тетушка на этом не успокоилась. Она стала вни­мательно следить за тем, сколько раз племянница упомянет в разговоре каждого из женихов. Допустим, ею получено следующее распределение упоминаний Агафьей Тихоновной женихов и их достоинств:

Никанор Иванович - 15 раз,

Иван Кузьмич - 6 раз,

Иван Павлович - 9 раз,

Балтазар Балтазарыч - 6 раз.

Тетушка уже видит, что похоже, Никанор Иванович ("уж такой великатный, а губы, мать моя, - малина, совсем малина") пользуется большей благосклонностью Агафьи Тихоновны, чем все остальные же­нихи. У нее есть два пути, чтобы это доказать статистически.

1) Суммировать все проявления благосклонности со стороны невесты: взгляды + упоминания в разговоре, - и сопоставить полученное рас­пределение с равномерным. Поскольку количество наблюдений воз­росло, есть шанс, что различия окажутся достоверными.

2) Сопоставить два эмпирических распределения - взгляда и упомина­ний в разговоре, - с тем, чтобы показать, что они совпадают между собой, то есть и во взглядах, и в словах Агафья Тихоновна придер­живается одинаковой системы предпочтений. Проанализируем оба варианта сопоставлений. В первом случае мы будем решать уже известную нам задачу со­поставления эмпирического распределения с теоретическим. Во втором случае мы будем сопоставлять два эмпирических распределения. Первый вариант развития шутливого примера: увеличение количества наблюдений

Вначале создадим таблицу эмпирических частот, в которой будут суммированы все замеченные проявления благосклонности невесты.

Таблица 4.3

Распределение проявлений благосклонности невесты между женихами

Женихи	Никанор Иванович	Иван Кузьмич	Иван Павлович	Балтазар Балтазарыч	Всего
Количество проявлений

Теперь сформулируем гипотезы.

Н₀: Распределение проявлений благосклонности невесты (взгляды и упо­минания в разговоре) не отличается от равномерного распределения. H₁: Распределение проявлений благосклонности невесты отличается от равномерного распределения.. Все расчеты произведем в таблице по алгоритму.

Таблица 4.4

Расчет критерия χ2 при сопоставлении проявлений благосклонности Агафьи Тихоновны с равномерным распределением

Разряды - женихи	Эмпирические частоты	Теоретическая частота суммарных проявлений	(fэj-fт)	(fэj-fт)^2	(fэj-fт)^2/ fт
	Ник. Ив. Ив. Куз. Ив. Пав. Бал. Бал.			-6 -6		8,47 2,12 2,12
Суммы					12,71

χ²_эмп=12,71

χ²_эмп> χ²_кр.

Ответ: H₀ отклоняется, принимается Н₁. Распределение прояв­лений благосклонности невесты между женихами отличается от равно­мерного распределения (р<0,01).

На этом примере мы убедились, что увеличение числа наблюде­ний повышает достоверность результата, если, конечно, в новых наблю­дениях воспроизводится прежняя тенденция различий.

Второй вариант развития шутливого примера: сопоставление двух эмпирических распределений

Теперь мы должны ответить на вопрос, одинаковая ли система предпочтений проявляется во взгляде Агафьи Тихоновны и ее словах?

Сформулируем гипотезы. Н₀: Распределения невербально и вербально выражаемых предпочтений не различаются между собой.

H₁: Распределения невербально и вербально выражаемых предпочтений различаются между собой.

Для подсчета теоретических частот нам теперь придется соста­вить специальную таблицу (Табл. 4.5). Ячейки в двух столбцах слева обозначим буквами. Для каждой из них теперь будет подсчитана особая, только к данной ячейке относящаяся, теоретическая частота. Это обу­словлено тем, что количества взглядов и словесных отзывов невесты о женихах неравны; взглядов 32, а словесных отзывов - 36. Мы должны всякий раз учитывать эту пропорцию.

Таблица 4.5

Эмпирические и теоретические частоты взглядов и упоминаний о жениха

Разряды - женихи	Эмпирические частоты	Суммы	Теоретические частоты
взгляда	Упоминаний в разговоре	взгляда	Упоминаний в разговоре
	Ник. Ив. Ив. Куз. Ив. Пав. Бал. Бал.	14 А 5 В 8 Д 5 Ж	15 Б 6 Г 9 Е 6 З		13,63 А 5,17 В 7,99 Д 5,17 Ж	15,37 Б 5,83 Г 9,01 Е 5,83 З
Суммы

Рассчитаем эту пропорцию. Всего проявлений благосклонности отмечено 68, из них 32 - взгляды и 36 - словесные высказывания. До­ля взглядов составит 32/68=0,47; доля упоминаний - 36/68=0,53.

Итак, во всех строках взгляды должны были бы составлять 0,47 всех проявлений по данной строке, а упоминания в разговоре - 0,53 всех проявлений. Теперь, зная суммы проявлений по каждой строке, мы можем рассчитать теоретические частоты для каждой ячейки Табл. 4.5.

f _Атеор=29*0,47=13,63

f _Бтеор=29*0,53=15,37

f _Втеор=11*0,47=5,17

f _Гтеор=11*0,53=5,83

f д_теор=17*0,47=7,99

f _Eтеор=17*0,53=9,01

f _Жтеор=110,47=5,17

f _Зтеор=11*0,53=5,83

Ясно, что сумма теоретических частот по строкам будет равнять­ся сумме всех проявлений по данной строке. Например,

f _Атеор+ f _Бтеор=13.63+15,37=29

f _Втеор+ f _Гтеор=5,17+5,83=11

f _Дтеор+ f _Етеор=7,99+9,01=17 и т.д.

При такого рода подсчетах лучше всякий раз себя проверить. Теперь мы можем вывести общую формулу подсчета f _теордля сопостав­ления двух или более эмпирических распределений:

Соответствующими строкой и столбцом будут та строка и тот столбец, на пересечении которых находится данная ячейка таблицы. Теперь нам лучше всего сделать развертку Табл. 4.5, представив все ячейки от А до Ж в виде первого столбца - это будет столбец эмпири­ческих частот. Вторым столбцом будут записаны теоретические часто­ты. Далее будем действовать по уже известному алгоритму. В третьем столбце будет представлены разности эмпирических и теоретических частот, в четвертом - квадраты этих разностей, а в пятом - результаты деления этих квадратов разностей на соответствующие каждой строке теоретические частоты. Сумма в нижнем правом углу таблицы и будет представлять собой эмпирическую величину % (Табл. 4.6).

Таблица 4.6

Расчет критерия χ2 при сопоставлении распределений невербальных и вербальных признаков благосклонности невесты

Ячейки таблицы частот	Эмпирическая частота взгляда (fэj)	Теоретическая частота (fт)	(fэj-fт)	(fэj-fт)^2	(fэj-fт)^2/ fт
	А Б В Г Д Е Ж З		13,63 15,37 5,17 5,83 7,99 9,01 5,17 5,83	+0,37 -0,37 -0,17 +0,17 +0,01 -0,01 -0,17 +0,17	0,14 0,14 0,03 0,02 0,00 0,00 0,03 0,02	0,01 0,01 0,01 0,00 0,00 0,00 0,01 0,00
Суммы					0,04

Число степеней свободы при сопоставлении двух эмпирических распределений определяется по формуле:

v =(k -1)·(c -1)

где k - количество разрядов признака (строк в таблице эмпири­ческих частот);

с - количество сравниваемых распределений (столбцов в таб­лице эмпирических частот).

В данном случае таблицей эмпирических частот является левая, эмпирическая часть таблицы 4.5, а не на ее развертка (Табл. 4.6). Количество разрядов - это количество женихов, поэтому k=4. Количество сопоставляемых распределений с=2. Итак, для данного случая,

v=(4-l)(2-t)=3

Определяем по Табл. IX Приложения 1 критические значения для ν=З:

Ответ: Н₀ принимается. Распределения невербально и вербально выражаемых невестой предпочтений не различаются между собой.

Итак, Агафья Тихоновна весьма последовательна в проявлении своих предпочтений, хотя, по-видимому, сама этого пока не замечает.

Иллюстрация 2

Третий вариант развития шутливого примера: сопоставление встречных выборов

К сожалению, в этом пункте мы от комедии вынуждены перейти к драме - истинной драме любви. Ибо, судя по тексту пьесы, прояв­ляемые женихами признаки влюбленности и симпатии по отношению к невесте отнюдь не соответствуют ее собственной системе предпочтений. У Ивана Павловича, а, главное, у Никанора Ивановича, которому не­вестой отдается столь явное предпочтение, проскальзывают в разговоре по большей части как раз отрицательные и задумчиво-неодобрительные отзывы о невесте: "Нос велик... Нет, не то, не то... Я даже думаю, что вряд ли она знакома с обхождением высшего общества. Да и знает ли она еще по-французски".

Благосклонных отзывов ("А сказать правду - мне понравилась она потому, что полная женщина" и т. п.) поступило:

от Никанора Ивановича - ни одного;

от Ивана Кузьмича - 15*

от Ивана Павловича - 6*

от Балтазара Балтазарыча - 18.

Попробуем ответить на вопрос: согласуются ли распределения (благосклонных отзывов невесты о женихах и женихов о невесте?

Мы видим, что это действительно особая задача. Мы сопостав­ляем два эмпирических распределения с совпадающей классификацией разрядов, но в одном случае это распределение реакций одного челове­ка на четверых других, а в другом случае это реакции четырех человек на одного и того же человека.

Такая модель взаимных реакций может использоваться отнюдь не только в области брачных консультаций, но и в решении задач "построения команды", выбора заместителя, подбора пар в тех видах деятельности, где требуется активное постоянное взаимодействие, в ис­следованиях социальной перцепции и взаимного влияния, в тренинге сенситивности и др.

Сформулируем гипотезы.

Н₀: Распределение положительных отзывов невесты совпадает с рас­пределением положительных отзывов женихов.

H₁: Распределение положительных отзывов невесты не совпадает с распределением положительных отзывов женихов.

Построим таблицу для подсчета теоретических частот.

Таблица 4.7

Эмпирические и теоретические частоты положительных высказываний невесты о женихах и женихов о невесте

	Эмпирические частоты	Суммы	Теоретические частоты
Разряды-женихи	Положительных высказываний невесты о женихах	Положительных высказываний женихов о невесте	Положительных высказываний невесты о женихах	Положительных высказываний женихов о невесте
	Ник. Ив. Ив. Куз. Ив. Пав. Бал. Бал.	15 А 6 В 9 Д 6 Ж	0 Б 15 Г 6 Е 18 З		7,20 А 10,08 В 7,20 Д 11,52 Ж	7,80 Б 10,92 Г 7,80 Е 12,48 З
Суммы

Теоретические частоты рассчитываем по уже известной формуле:

f _{а теор}=15*36/75=7,20

f _{Б теор}=15*39/75=7,80

f _{В теор}=21*36/75=10,08

f _{Г теор}=21*39/75=10,92

f _{Д теор}=15*36/75=7,20

f _{Е теор}=15*39/75=7,80

f _{Ж теор}=24*36/75=11,52

f _{З теор}=24*39/75=12,48

Суммы теоретических частот по строкам совпадают. Все даль­нейшие расчеты выполним в таблице по алгоритму.

Таблица 4.8

Расчет критерия χ2 при сопоставлении распределений высказываний невесты о женихах и женихов о невесте

Ячейки таблицы частот	Эмпирическая частота взгляда (fэj)	Теоретическая частота (fт)	(fэj-fт)	(fэj-fт)^2	(fэj-fт)^2/ fт
	А Б В Г Д Е Ж З		7,20 7,80 10,08 10,92 7,20 7,80 11,52 12,48	+7,80 -7,80 -4,08 +4,08 +1,80 -1,80 -5,52 +5,52	60,84 60,84 16,65 16,65 3,24 3,24 30,47 30,47	8,45 7,80 1,65 1,52 0,45 0,42 2,64 2,44
Суммы					25,37

Определим число степеней свободы V по количеству строк k и столбцов с в левой части Табл. 4.7: (k =4, c=2).

v=(k-1)(c-1)

Критические значения χ2 для ν=3 нам уже известны:

Ответ: Н₀ отвергается. Принимается H₁. Распределение положительных отзывов предпочтений невесты не совпадает с распределени­ем положительных отзывов женихов (ρ<0,01).

Итак, если бы Иван Кузьмич Подколесин не сбежал, Агафью Тихоновну могло бы ожидать не меньшее разочарование: предпочитаемый ею Никанор Иванович, "тонкого поведения человек", ее отвергает.

Мы не рассмотрели лишь третью группу возможных гипотез в методе χ2. Они, как мы помним, касаются сопоставлений одновременно 3 и более распределений. Принцип расчетов там такой же, как и при сопоставлении двух эмпирических распределений. Это касается и фор­мулы расчета теоретических частот, и алгоритма последующих расчетов.

Рассмотрим особые случаи в применении метода χ2.

1. В случае, если число степеней свободы ν=l, т. е. если признак принимает всего 2 значения, необходимо вносить поправку на непрерывность[16].

2. Если признак варьирует в широком диапазоне (например, от 10 до
140 сек. и т.п.), возникает необходимость укрупнять разряды.

Дата добавления: 2017-01-14