Пример 1 - сопоставление выборок по качественно определяемому признаку

Гипотезы

Описание критерия

Критерий оценивает достоверность различий между процентными долями двух выборок, в которых зарегистрирован интересующий нас эффект.

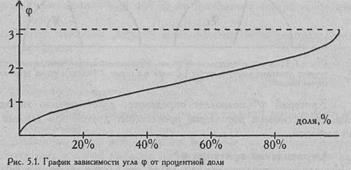
Суть углового преобразования Фишера состоит в переводе процент­ных долей в величины центрального угла, который измеряется в радианах. Большей процентной доле будет соответствовать больший угол ф, а меньшей доле - меньший угол, но соотношения здесь не линейные:

где Р - процентная доля, выраженная в долях единицы (см. Рис. 5.1).

При увеличении расхождения между углами φ₁ и φ₂ и увеличе­ния численности выборок значение критерия возрастает. Чем больше величина φ*, тем более вероятно, что различия достоверны.

H₀: Доля лиц, у которых проявляется исследуемый эффект, в выборке 1 не больше, чем в выборке 2.

H₁: Доля лиц, у которых проявляется исследуемый эффект, в выборке 1 больше, чем в выборке 2.

Графическое представление критерия φ*

Метод углового преобразования несколько более абстрактен, чем остальные критерии.

Формула, которой придерживается Е. В. Гублер при подсчете значений φ, предполагает, что 100% составляют угол φ=3,142, то есть округленную величину π=3,14159... Это позволяет нам представить со­поставляемые выборки в виде двух полукругов, каждый из которых символизирует 100% численности своей выборки. Процентные доли испытуемых с "эффектом" будут представлены как секторы, образован­ные центральными углами φ. На Рис. 5.2 представлены два полукруга, иллюстрирующие Пример 1. В первой выборке 60% испытуемых ре­шили задачу. Этой процентной доле соответствует угол φ=1,772. Во второй выборке 40% испытуемых решили задачу. Этой процентной доле соответствует угол φ =1,369.

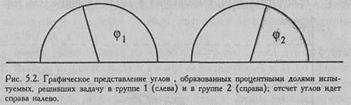
Критерий φ* позволяет определить, действительно ли один из углов статистически достоверно превосходит другой при данных объе­мах выборок.

Ограничения критерия φ*

1. Ни одна из сопоставляемых долей не должна быть равной нулю. Формально нет препятствий для применения метода φ в случаях, когда доля наблюдений в одной из выборок равна 0. Однако в этих случаях результат может оказаться неоправданно завышенным (Гублер Е.В., 1978, с. 86).

2. Верхний предел в критерии φ отсутствует - выборки могут быть сколь угодно большими.

Нижний предел - 2 наблюдения в одной из выборок. Однако должны соблюдаться следующие соотношения в численности двух выборок:

а) если в одной выборке всего 2 наблюдения, то во второй должно быть не менее 30:

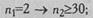
б) если в одной из выборок всего 3 наблюдения, то во второй должно быть не менее 7:

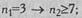
в) если в одной из выборок всего 4 наблюдения, то во второй должно быть не менее 5:

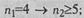
г) при n₁,n₂≥5 возможны любые сопоставления.

В принципе возможно и сопоставление выборок, не отвечающих этому условию, например, с соотношением n₁ =2, n₂ ⁼15, но в этих слу­чаях не удастся выявить достоверных различий.

Других ограничений у критерия φ* нет.

Рассмотрим несколько примеров, иллюстрирующих возможности

критерия φ*.

Пример 1: сопоставление выборок по качественно определяемому при­знаку.

Пример 2: сопоставление выборок по количественно измеряемому при­знаку.

Пример 3: сопоставление выборок и по уровню, и по распределению признака.

Пример 4: использование критерия φ* в сочетании с критерием X Колмогорова-Смирнова в целях достижения максимально точного результата.

В данном варианте использования критерия мы сравниваем про­цент испытуемых в одной выборке, характеризующихся каким-либо ка­чеством, с процентом испытуемых в другой выборке, характеризующих­ся тем же качеством.

Допустим, нас интересует, различаются ли две группы студентов по успешности решения новой экспериментальной задачи. В первой группе из 20 человек с нею справились 12 человек, а во второй выбор­ке из 25 человек - 10. В первом случае процентная доля решивших за­дачу составит 12/20·100%=60%, а во второй 10/25·100%=40%. Дос­товерно ли различаются эти процентные доли при данных n₁ и n₂?

Казалось бы, и "на глаз" можно определить, что 60% значи­тельно выше 40%. Однако на самом деле эти различия при данных n₁, n₂ недостоверны.

Проверим это. Поскольку нас интересует факт решения задачи, будем считать "эффектом" успех в решении экспериментальной задачи, а отсутствием эффекта - неудачу в ее решении.

Сформулируем гипотезы.

H₀: Доля лиц, справившихся с задачей, в первой группе не больше, чем во второй группе.

H₁: Доля лиц, справившихся с задачей, в первой группе больше, чем во второй группе.

Теперь построим так называемую четырехклеточную, или четы­рехпольную таблицу, которая фактически представляет собой таблицу эмпирических частот по двум значениям признака: "есть эффект" - "нет эффекта".

Таблица 5.1

Четырехклеточная таблица для расчета критерия при сопоставлении двух групп испытуемых по процентной доле решивших задачу.

Группы	"Есть эффект": задача решена	"Нет эффекта": задача не решена	Суммы
	Количество испытуемых	% доля		Количество испытуемых	% доля
1 группа		(60%)	А		(40%)	Б
2jЈynna		(40%)	В		(60%)	Г
Суммы

В четырехклеточной таблице, как правило, сверху размечаются столбцы "Есть эффект" и "Нет эффекта", а слева - строки "1 группа" и "2 группа". Участвуют в сопоставлениях, собственно, только поля (ячейки) А и В, то есть процентные доли по столбцу "Есть эффект".

По Табл. XII Приложения 1 определяем величины φ, соответст­вующие процентным долям в каждой из групп.

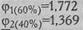
Теперь подсчитаем эмпирическое значение φ* по формуле:

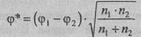
где φ₁ - угол, соответствующий большей % доле;

φ₂ - угол, соответствующий меньшей % доле;

n₁ - количество наблюдений в выборке 1;

n₂ - количество наблюдений в выборке 2.

В данном случае:

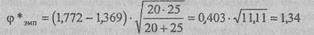
По Табл. XIII Приложения 1 определяем, какому уровню значи­мости соответствует φ*_эмп=1,34:

р=0,09

Можно установить и критические значения φ*, соответствующие принятым в психологии уровням статистической значимости:

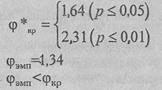
Построим "ось значимости".

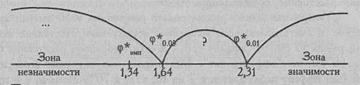
Полученное эмпирическое значение φ* находится в зоне незна­чимости.

Ответ: H₀ принимается. Доля лиц, справившихся с задачей, впервой группе не больше, чем во второй группе.

Можно лишь посочувствовать исследователю, который считает существенными различия в 20% и даже в 10%, не проверив их досто­верность с помощью критерия φ*. В данном случае, например, досто­верными были бы только различия не менее чем в 24,3%.

Похоже, что при сопоставлении двух выборок по какому-либо качественному признаку критерий φ может нас скорее огорчить, чем обрадовать. То, что казалось существенным, со статистической точки зрения может таковым не оказаться.

Гораздо больше возможностей порадовать исследователя появля­ется у критерия Фишера тогда, когда мы сопоставляем две выборки по количественно измеренным признакам и можем варьировать "эффект.

Дата добавления: 2017-01-14