
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Оптимізаційні моделі
|
|
|
|
У практиці обґрунтування інженерних рішень важливе місце займають оптимізаційні задачі з використанням детермінованих моделей.
Структура оптимізаційної моделі в загальному випадку включає цільову функцію F(х), яку необхідно мінімізувати або максимізувати, обмеження hk(х) у вигляді рівнянь, обмеження gj(x) у вигляді нерівностей, а також область S допустимих значень незалежних змінних хi. Для спрощення викладу будемо вважати, що оптимізація передбачає мінімізацію цільової функції F(х). Тоді математичну модель у загальному вигляді можна записати так:
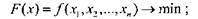 (7.1)
(7.1)
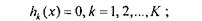 (7.2)
(7.2)
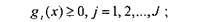 (7.3)
(7.3)
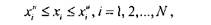 (7.4)
(7.4)
де хiн та хiв — нижнє та верхнє значення i-ї змінної.
Функція F(x) може мати локальний і глобальний мінімуми (рис. 7.1). Локальний мінімум функції F(x) існує в точці х0, якщо для всіх значень х у діапазоні х0 ± δ справедлива нерівність F(x) ≥ F(x0). Функція F(x) має глобальний мінімум в точці х*, якщо для всіх х справедлива нерівність F(x) ≥ F(x*).
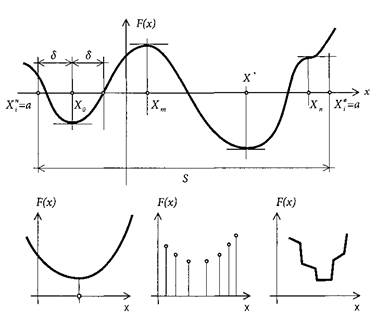
Рис. 7.1. Приклади функцій однієї змінної: а — неперервна функція з локальним (х0) і глобальним (х*) мінімумом у допустимій області S; б — неперервна унімодальна функція; в — дискретна унімодальна функція; г — унімодальна функція з розривами.
Якщо функція F(x) на відрізку а < х< b має лише одну точку мінімуму х*, по обидві сторони від якої функція монотонно зростає, то така функція називається унімодальною (рис. 7.1, б). Унімодальні функції можуть бути не лише неперервними, але й дискретними, мати розриви. Проте для них також повинна бути справедливою умова F(x) ≥ F(x*).
Одномірна оптимізація без обмежень характеризується наявністю однієї змінної і відсутністю обмежень hk(х) i gj(х), тобто
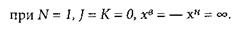 (7.5)
(7.5)
Задачі цього класу інакше називають безумовною оптимізацією, бо в них відсутні додаткові умови.
У випадках коли F(x) є функцією декількох аргументів (тобто N > 1), а всі інші умови відповідають задачі типу (3.5), то має місце багатомірна задача безумовної оптимізації.
Задачі умовної оптимізації, в яких функції пк(х) і gj(х) є лінійними, відносяться до класу задач з лінійними обмеженнями. В них цільова функція може бути нелінійною і тоді їх називають задачами нелінійного програмування.
Якщо ж і цільова функція, і обмеження лінійні, то такі задачі відносяться до лінійного програмування. При додатковій умові, що всі або окремі змінні вектора X повинні бути цілими числами, задачі відносяться до цілочисельного програмування.
Наведена вище класифікація оптимізаційних задач має не лише методологічне, але й практичне значення, бо передбачає використання специфічних методів їх вирішення. Постановку оптимізаційних задач рекомендується здійснювати в такій послідовності.
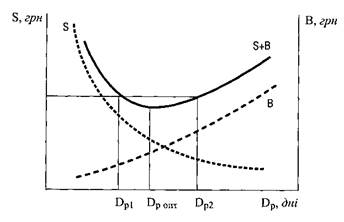
Рис. 7.2. Залежність затрат на придбання і утримання техніки (S) і втрат врожаю (В) від тривалості збирання.
Спочатку необхідно визначити границі системи, що оптимізується. Від цього суттєво залежать зміст і складність задачі. Наприклад, при обґрунтуванні складу збирально-транспортного комплексу можна оптимізувати розмір збиральних ланок, а всі інші ланки розрахунковими методами узгодити з основними. Такий вибір границь системи дозволяє вирішувати простішу оптимізаційну задачу, ніж при оптимізації всього ЗТК.
Наступним кроком буде обґрунтування критерію оптимальності, який однозначно і з достатньою повнотою характеризував би мету оптимізації. Призначення критерію є одним з найбільш відповідальних етапів.
Наприклад, при оптимізації потреби у збиральній техніці критерієм може бути сума затрат на придбання та експлуатацію техніки (S) і втрат (В) від недобору врожаю внаслідок збільшення строків збирання при недостатній кількості технічних засобів. У порівнянні з окремими складовими S і В їх сума (S+В) є більш представницькою у відношенні до мети і в певних границях має оптимум (рис. 7.2).
Далі обґрунтовують набір незалежних змінних, які суттєво впливають на величину критерію оптимальності, а також обмеження. Від повноти включення незалежних змінних (факторів) у математичну модель задачі значною мірою залежить адекватність моделі реальній системі. З іншого боку, важливо не збільшувати розмірності задачі за рахунок надлишкової деталізації моделі, включення факторів, що незначно впливають на цільову функцію.
Математична модель задачі описує взаємозв’язки між факторами і відображає їх вплив на цільову функцію. Ці взаємозв’язки виражаються рівняннями, що описують фізичні процеси функціонування системи, а також сукупністю обмежень у вигляді рівнянь та нерівностей, які визначають область допустимих значень факторів, задають величину ресурсів і додаткові вимоги. Крім числа факторів, що включені в модель, на її адекватність впливає також аналітичний вираз рівнянь зв’язку. Так, спрощення моделі за рахунок виразу суттєво нелінійних зв’язків лінійними залежностями може призвести до неадекватності моделі. Таким чином, побудова математичної моделі вимагає розуміння суті процесів, що протікають у системі, а також вимог щодо точності кінцевих результатів оптимізацїї.
Після того, як визначені границі системи, обґрунтований критерій та цільова функція, побудована математична модель, постає питання вибору методу оптимізації. Значною мірою цей вибір залежить від класу задачі, тобто конкретного виразу загальної моделі, що описується функціями (7.1—7.4). Найпоширеніші в інженерній практиці методи оптимізації розглянемо детальніше пізніше.
|
|
|
|
|
Дата добавления: 2015-07-13; Просмотров: 952; Нарушение авторских прав?; Мы поможем в написании вашей работы!