Лінійне програмування

Серед методів багатомірної оптимізації з обмеженнями особливе міс­це займає лінійне програмування (ЛП). Це пояснюється широким колом задач, що можуть бути зведені до лінійних моделей, а також розвинутим математичним і програмним забезпеченням методу ЛП.

Задача ЛП у стандартній формі має вигляд:

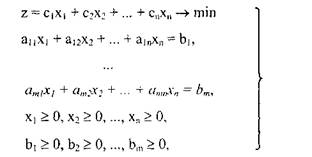(7.14)

де п - число незалежних змінних;

т - число обмежень;

a_i, c_i - числові коефіцієнти при змінній x_i.

Застосування загальних методів розв’язання задач ЛП потребує зве­дення математичних моделей до певного однотипного вигляду.

У загальному випадку обмеження можуть бути задані у вигляді нерів­ностей і рівнянь. При цьому в нерівностях ліва і права частини можуть бути зв’язані знаками ≥ і ≤. Змінні, що входять у математичну модель, мо­жуть бути додатними або не мати обмежень у знаку. Це породжує певну різноманітність математичних моделей, які можуть бути зведені до стан­дартної форми лінійних оптимізаційних моделей. Стандартна форма пе­редбачає, що всі обмеження записуються у вигляді рівнянь з додатньою правою частиною; значення всіх змінних моделі також є додатніми; цільо­ву функцію потрібно мінімізувати або максимізувати.

Будь-яку лінійну модель можна звести до стандартної форми, вико­ристовуючи наступні прийоми.

Звести нерівності до рівняння можна шляхом введення додаткової змінної, абсолютне значення якої дорівнює різниці між лівою і правою частинами. Ця змінна додається до лівої частини якщо має місце нерів­ність типу ≤. Якщо вихідне обмеження є нерівністю типу ≥, то додаткова зміна віднімається від лівої частини.

Приклад: Нехай вихідне обмеження має вигляд:

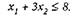
Тоді після введення додаткової змінної s₁ > 0, можемо перейти до рівняння:

Приклад: Вихідне, обмеження х x₁+2х₂-5х³≥15 зводиться до рівняння введенням додаткової змінної s₂:

У першій вимозі стандартної форми обумовлене додатне (невід’ємне) значення правої частини. Якщо ця вимога не задовольняється, то ліву і праву частини рівняння множать на -1.

Приклад: Рівняння 7х₁+4х₂-3х₃=-6 еквівалентне рівнянню -7х₁-4х₂+3х₃=+6.

Будь яку змінну х_i що не має обмежень у знаку, можна подати, як різницю двох невід’ємних змінних:

х_i = х'_і-х"_i, де х'_і ≥ 0, х"_i ≥ 0.

Таку підстановку потрібно зробити у всі обмеження і цільову функ­цію, що містять змінну х_i. Важливою особливістю змінних х'_і та х"_і є те, що лише одна з них є більшою від нуля, інша ж дорівнює нулю.

Процес розв’язання задачі ЛП симплекс-методом має ітераційний характер. У схемі обчислень реалізується впорядкована послідовність визначення значень цільової функції в кутових точках (вершинах) багато­гранника доти, поки не буде знайдена точка, що відповідає оптимальному рішенню. У послідовності розрахунків дотримуються правил:

• кожна наступна точка повинна бути суміжною з попередньою;

• зворотний перехід до попередньої точки не допускається.

• максимальне число ітерацій, тобто розрахунків, у конкретній ку­товій точці не перевищує

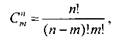
де т — число обмежень;

п — число незалежних змінних.

Питання опису алгоритму і суті обчислювальних процедур симплекс - методу достатньо висвітлені в підручниках і спеціальній літературі. В да­ному посібнику звертається увага на правильну постановку задач ЛП з на­ступним їх вирішенням на ПЕОМ, програмне забезпечення яких включає симплекс-метод.

Дата добавления: 2015-07-13