Проверка гипотезы. Сравнение двух дисперсий нормальных генеральных совокупностей

Сравнение двух дисперсий нормальных генеральных совокупностей.

Проверка различных статистических гипотез

Постановка задачи. По независимым выборкам, объемы которых 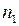и , извлеченным из нормальных генеральных совокупностей, найдены исправленные выборочные дисперсии и . Требуется сравнить эти дисперсии.

Прямая гипотеза 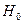: D(X) = D(Y)

Критерий проверки гипотезы:

(отношение большей исправленной дисперсии к меньшей)

имеет распределение Фишера—Снедекора, число степеней свободы

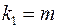- число степеней свободы большей исправленной дисперсии;

, - число степеней свободы меньшей исправленной дисперсии)

Выбрать уровень значимости α.

Правило 1. Если прямая и альтернативная гипотезы имеют вид

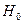: D(X) = D(Y)

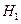: D (X) > D (Y),, то

критическую точку ищут по уровню значимости и числам степеней свободы

Если , то признается правильной гипотеза 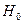, если же , то признается правильной гипотеза .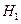

Правило 2. Если прямая и альтернативная гипотезы имеют вид

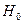: D(X) = D(Y)

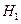: D (X) ≠ D (Y),, то

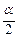критическую точку ищут по уровню значимости и числам степеней свободы

Если 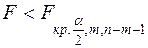, то признается правильной гипотеза 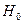, если же , то признается правильной гипотеза .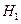

Проведены измерения пульса у больных, подвергнутых некоторой лечебной процедуре, а также у больных контрольной группы. Статистическая обработка результатов показала, что несмещенная оценка дисперсии частоты пульса больных первой группы составила (уд/мин)², у больных второй группы – (уд/мин)². Предполагая, что значения пульса у подобных больных распределены по нормальному закону, при уровне значимости 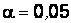проверить значимость различия между оценками дисперсий.

Решение. Итак, необходимо проверить нулевую гипотезу относительно альтернативной . Поскольку исправленная выборочная дисперсия значений пульса у больных первой группы превышает соответствующую оценку для больных второй группы, то по формуле для статистики получим:

Поскольку альтернативная гипотеза задает двустороннюю критическую область, число степеней свободы числителя равно , а знаменателя – для по таблице распределения Фишера-Сне­де­­кора (прил. 5) найдем критическое значение статистики: .

Экспериментальное значение критерия меньше критического (попало в область принятия нулевой гипотезы), следовательно, проверяемая гипотеза не противоречит опытным данным, и при уровне значимости 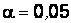наблюдаемое различие в оценках дисперсии следует считать незначимым.

Предложена новая технология изготовления ламп, утверждается, что она обеспечивает меньший технологический разброс светоотдачи, чем старая. Для проверки изготовлено n = 9 ламп по старой технологии: они имеют значения светоотдачи (лм/Вт):

x: 62, 73, 80, 79, 63, 77, 81, 75, 62;

и m = 10 ламп по новой технологии, их светоотдача:

y: 75, 78, 77, 68, 73, 79, 72, 71, 86, 79.

Формулируем гипотезу: технологический разброс одинаков, т.е. Dх = Dу. Критерий проверки F (3.4). Выберем уровень значимости α = 0.05. По таблице находим F_q.

Если окажется, что S_x² > S_у², k₁ = 8, k₂ = 9, то F_q = 3.23.

Если S_у² > S_x², k₁ = 9, k₂ = 8, то F_q = 3.39.

Вычисляем: = 72.4
= 63.5

=75.8
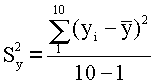= 25.3

F_э = 63.5 / 25.3 = 2.51. Вывод: F_э < F_q.

Гипотеза о равенстве дисперсий светоотдачи при изготовлении ламп по старой и новой технологии проверена по критерию Фишера на уровне значимости 0.05 и принята. (Если разработчики все же настаивают на преимуществах новой технологии, следует провести новый эксперимент с выборками больших объемов).

Дата добавления: 2015-07-13