Проверка гипотезы. Критерий проверки гипотезы:

Прямая гипотеза :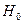

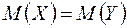
Критерий проверки гипотезы:

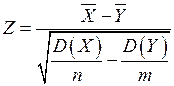имеет нормальное распределение

Выбрать уровень значимости α.

Правило 1. Если прямая и альтернативная гипотезы имеют вид

:

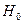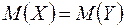
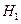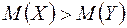: , то

критическую точку 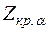ищут из равенства 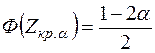по таблице значений функции Лапласа

Если 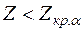, то признается правильной гипотеза 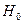, если же 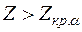, то признается правильной гипотеза .

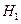Правило 2. Если прямая и альтернативная гипотезы имеют вид

:

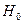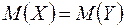
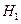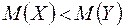: ,, то

критическую точку 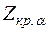ищут также из равенства 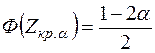по таблице значений функции Лапласа

Если 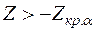, то признается правильной гипотеза 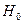, если же 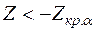, то признается правильной гипотеза .

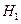Правило 3. Если прямая и альтернативная гипотезы имеют вид

:

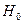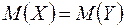
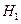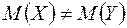: ,, то

Критическую точку 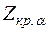ищут из равенства 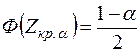по таблице значений функции Лапласа

Если 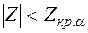, то признается правильной гипотеза 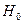, если же 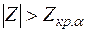, то признается правильной гипотеза .

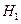Замечение:

Эту же статистику используют и при проверке гипотезы о равенстве вероятностей «успеха». Объемы выборок 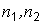должны быть достаточно велики, чтобы биномиальное распределение можно было бы приближенно считать нормальным

Пример Рабочий в начале смены настроил два станка-автомата: X и Y. Предварительным анализом было установлено, что размер диаметра валиков, изготовленных каждым автоматом, имеет нормальный закон распределения с дисперсией 5 мм для станка X и 7 мм для станка Y. В конце смены был проведен выборочный контроль 14 деталей, обработанных на станке X, и 9 де-талей - на станке Y. Средние диаметры валиков соответственно составили: для автомата X – 182 мм, для Y – 185 мм. Проверить гипотезу о том, что два станка-автомата настроены на один размер.

1. Принимаем :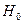

: .

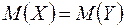
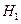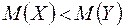2. Назначаем. Ур значимости 0,01

3. Согласно проверяемой гипотезе в основе проверки лежит критерий:

4. Согласно гипотезе критическая область W – левосторонняя

Сравнение двух средних нормальных генеральных совокупностей, дисперсии которых неизвестны и одинаковы (малые независимые выборки)

Обозначим через 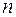и 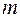объемы малых ( 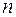< 30, 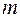< 30) независимых выборок, по которым найдены соответствующие выборочные средние 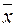и 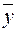и исправленные выборочные дисперси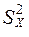и и 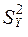Генеральные дисперсии хотя и неизвестны, но предполагаются одинаковыми (т.е. требуется предварительная проверка гипотезы о равенстве дисперсий).

Дата добавления: 2015-07-13