
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Проверка гипотезы. Критерий проверки гипотезы:
|
|
|
|
Прямая гипотеза 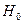 :
: 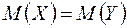
Критерий проверки гипотезы:
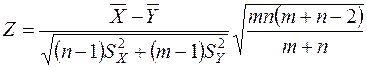 имеет распределение Стьюдента с числом степеней свободы
имеет распределение Стьюдента с числом степеней свободы 
Выбрать уровень значимости α.
Правило 1. Если прямая и альтернативная гипотезы имеют вид
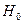 :
: 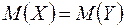
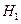 :
: 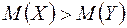 , то
, то
критическую точку  ищут в таблице критических точек распределения Стьюдента по заданному уровню значимости
ищут в таблице критических точек распределения Стьюдента по заданному уровню значимости  , помещенному в верхней строке таблицы, и числу степеней свободы
, помещенному в верхней строке таблицы, и числу степеней свободы 
Если  , то признается правильной гипотеза
, то признается правильной гипотеза 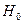 , если же
, если же  , то признается правильной гипотеза
, то признается правильной гипотеза 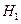 .
.
 Правило 2. Если прямая и альтернативная гипотезы имеют вид
Правило 2. Если прямая и альтернативная гипотезы имеют вид
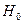 :
: 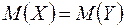
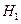 :
: 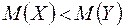 , то
, то
критическую точку  ищут по таблице критических точек распределения Стьюдента
ищут по таблице критических точек распределения Стьюдента
Если  , то признается правильной гипотеза
, то признается правильной гипотеза 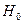 , если же
, если же  , то признается правильной гипотеза
, то признается правильной гипотеза 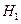 .
.

Правило 3. Если прямая и альтернативная гипотезы имеют вид
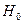 :
: 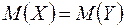
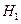 :
: 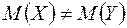 ,, то
,, то
критическую точку  ищут по таблице критических точек распределения Стьюдента
ищут по таблице критических точек распределения Стьюдента
Если  , то признается правильной гипотеза
, то признается правильной гипотеза 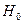 , если же
, если же  , то признается правильной гипотеза
, то признается правильной гипотеза 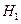 .
.

Пример. Техническая норма предусматривает в среднем 40 с на выполнение определенной технологической операции на конвейере по производству часов. От работающих на этой операции поступили жалобы, что они в действительности затрачивают на нее больше времени. Для проверки данной жалобы произведены хронометрические измерения времени выполнения этой технологической операции у 16 работниц, занятых на ней, и получено среднее время выполнения операции X = 42 с. Можно ли по имеющимся хронометрическим данным на уровне значимости = 0,01 отклонить гипотезу о том, что среднее время выполнения этой операции соответствует норме, если:
а) исправленное выборочное среднее квадратическое отклонение s – 3,5 с;
б) выборочное среднее квадратическое отклонение 3,5 с?
Решение, а) Для решения данной задачи необходимо проверить гипотезу о том, что неизвестная генеральная средняя нормальной совокупности точно равна определенному числу, когда дисперсия генеральной совокупности неизвестна (выборка мала, так как n = 16 меньше 30).
Сформулируем нулевую и конкурирующую гипотезы согласно условию задачи.
Н 0: а = а0 = 40 – неизвестное математическое ожидание а (нормально распределенной генеральной совокупности с неизвестной дисперсией) равно гипотетически предполагаемому числовому значению а0 (применительно к условию данной задачи - время выполнения технологической операции соответствует норме).
Н 1: а > 40 – неизвестное математическое ожидание а (нормально распределенной генеральной совокупности с неизвестной дисперсией) больше числового значения а0 (применительно к условию данной задачи – время выполнения технологической операции больше установленной нормы).
Так как конкурирующая гипотеза – правосторонняя, то и критическая область – правосторонняя.
В качестве критерия для сравнения неизвестного математического ожидания а (нормально распределенной генеральной совокупности с неизвестной дисперсией) с гипотетическим числовым значением а0 используется случайная величина t -критерий Стьюдента. (Приложение 2).
Его наблюдаемое значение (t набл) рассчитывается по формуле
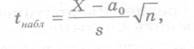
где X – выборочная средняя; а0 – числовое значение генеральной средней; s – исправленное среднее квадратическое отклонение; n – объем выборки.
Найдем наблюдаемое значение t набл
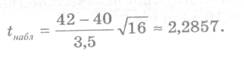
Критическое значение (t кр) следует находить с помощью таблиц распределения Стьюдента (приложение 2) по уровню значимости и числу степеней свободы k.
По условию = 0,01; число степеней свободы найдем по формуле
k = n - 1,
где k - число степеней свободы; n - объем выборки.
k = 16 - 1 = 15.
Найдем t кр по уровню значимости = 0,01 (для односторонней критической области) и числу степеней свободы k = 15:
t кр(0=;10, k =15)= 2,6
Заметим, что при левосторонней конкурирующей гипотезе Н1: а < 40 t кр следует находить по таблицам распределения Стьюдента (приложение 2) по уровню значимости (для односторонней критической области) и числу степеней свободы k = n – 1 и присваивать ему знак «минус».
При двусторонней конкурирующей гипотезе Н1: а≠40t следует находить по таблицам распределения Стьюдента (приложение 2) по уровню значимости а (для двусторонней критической области) и числу степеней свободы k = n – 1.
t набл < t кр следовательно, на данном уровне значимости нет оснований отклонить нулевую гипотезу.
Ответ. По имеющимся хронометрическим данным на уровне значимости а = 0,01 нельзя отклонить гипотезу о том, что среднее время выполнения этой операции соответствует норме. Следовательно, жалобы работниц - необоснованны.
|
|
|
|
|
Дата добавления: 2015-07-13; Просмотров: 695; Нарушение авторских прав?; Мы поможем в написании вашей работы!