Функция Гаусса

В математике функция, график которой имеет форму колоколообразной кривой, называется функцией нормального распределения или функцией Гаусса. Она имеет следующий вид:

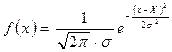(4.1)

Функция Гаусса описывает предельное распределение результатов измерений величины x, истинное значение которой равно X. Причем при измерении величины x оказываются только случайные ошибки. Принято считать, что результаты измерений распределены нормально, если их предельное распределение описывается функцией Гаусса.

В формуле (4.1) величина σ является фиксированным параметром, который определяет ширину гауссовой кривой в точках перегиба. Малые значения σ приводят к распределению типа острого пика, которое соответствует более точным измерениям, в то время как большие значения σ дают широкое распределение, соответствующее измерениям с малой точностью. На Рис.6 представлены два примера графиков функций Гаусса с различными значениями величин Х и σ. Видно, что величина σ в знаменателе предэкспоненциального множителя формулы (4.1) обеспечивает для более узкого распределения (малые σ) большую высоту в точке x = X. Это обусловлено тем, что функция Гаусса нормирована, то есть для нее выполнено условие (3.1.6). Поэтому площадь под кривой, выражающей на графике функцию Гаусса, при любых значениях σ и X должна равняться единице.

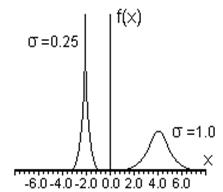Рис. 6

Функция Гаусса отражает следующие предположения, лежащие в основе теории случайных погрешностей и подтверждаемые опытом:

1. Погрешности результатов наблюдений принимают непрерывный ряд значений.

2. При большом числе наблюдений одинаково часто встречаются погрешности одного значения, но разных знаков.

3. Частота появления погрешностей уменьшается с возрастанием их значений.

В случае распределения Гаусса среднее значение величины X определяется, согласно

(3.1.5), по формуле:

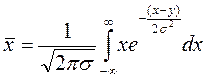(4.2)

Интеграл можно вычислить, что приведёт к следующему результату:

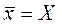(4.3)

Отсюда можно сделать вывод: если результаты измерений распределены в соответствии с функцией Гаусса, то в случае бесконечно большого числа измерений среднее значение

будет равно истинному значению 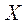, которое соответствует центру функции Гаусса.

Для дисперсии (3.1.9) в случае распределения Гаусса получим

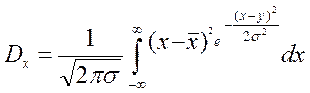(4.4)

Результат интегрирования:

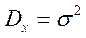(4.7)

Поскольку согласно (3.1.10), корень из дисперсии есть стандартное отклонение, то

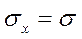(4.8)

Следовательно: параметр 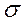ширины функции Гаусса есть стандартное отклонение, которое мы получили бы в случае бесконечно большего числа измерений.

Дата добавления: 2015-07-13