Отбрасывание результаттов прямых измерений

Ранее было сказано, что среди погрешностей измерений могут встречаться промахи – погрешности, существенно превышающие ожидаемые значения при данных условиях эксперимента. Поэтому возникает естественный вопрос – какие погрешности можно считать промахами с целью исключения в дальнейшем соответствующих им результатов измерения? Эта оценка осуществляется на основе критерия Шовене.

Пусть проделано N измерений некой величины x и получены следующие результаты: . На основании этих значений по формулам (7.1) и (7.2) можно вычислить 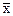и . Если имеется подозрительный результат, погрешность которого, возможно, является промахом, то для него вычисляют

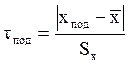(8.1)

число выборочных стандартных отклонений, на которое 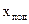отличается от 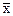. По таблице 2 Приложения можно найти вероятность Р(вне 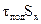) того, что нормальное измерение будет отличаться от 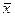на 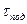или более выборочных стандартных отклонений. Наконец, следует умножить полученную вероятность Р(вне 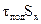) на полное число измерений N, чтобы получить

n(хуже, чем 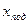) = N*P(вне 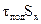), (8.2)

которое определяет число ожидаемых измерений, которые дают столь же плохие результаты, что и 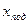. Если n меньше 0,5, то 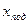отбрасывается. В этом состоит критерий Шовене. После отбрасывания результата, не удовлетворяющего критерию Шовене, надо пересчитать 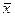и 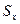по оставшимся данным. При n большем 0,5 следует всё оставить без измерения.

Рассмотрим пример: произведено шесть измерений некоторой величины и получены следующие результаты:

3,8; 3,5; 3,9; 3,9; 3,4; 1,8.

Среди этих результатов подозрительным является 1,8. Поэтому с учётом шести измерений рассчитываем 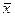=3,4 и 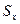=0,8. Значение 1,8 отличается от 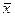на 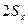. Согласно таблицы 1 Приложения:

Р(вне 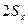)=1-Р(в пределах 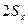) = 0,05.

То есть из двадцати возможных результатов измерений приблизительно только один должен также сильно отличаться от 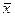, как число 1,8. в случае проведённых шести измерений ожидаемое число таких результатов n=0,05, 6=0,3. Поскольку n<0,5, то, согласно критерию Шовене, подозрительный результат x=1,8 должен быть исключён, а для оставшихся значений 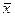=3,7, 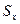=0,23.

Дата добавления: 2015-07-13