Распределение Стьюдента

КОСВЕННЫЕ ИЗМЕРЕНИЯ

И, наконец, следует привести результаты, которые получены в теории измерений для случая, когда производятся косвенные измерения величины q(x,y,….z). Причём величины x,y,….z могут быть зависимыми. Пусть производится конечное число измерений, но на результат измерений оказывает влияние только случайные погрешности. Если погрешности при измерении x,y,….z малы, то существует строгое доказательство, что наилучшей оценкой значения q является

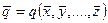(9.1)

где 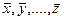определяются по формуле (6.1).

Оценка стандартного отклонения при косвенных измерениях определяются выражением:

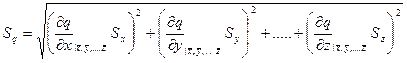(9.2)

где 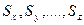являются выборочными стандартными отклонениями, определяемыми по формуле (3.4.2). Частные производные вычисляются при , .

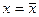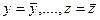Ранее было показано, что величина 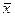является лишь наилучшей оценкой истинного значения измеряемой величины. Вместе с этим, наилучшей оценкой стандартного отклонения среднего является величина 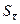. Таким образом мы имеем дело с некоторыми приближениями. Ясно, что распределение случайных погрешностей будет тем существенней отличаться от функции Гаусса, чем меньше выполнено измерений.

Английский химик и математик В.С. Госсет, публиковавший свои работы под псевдонимом Стьюдент, получил формулу для нахождения распределения погрешностей средних значений, получаемых при конечном числе измерений. Причём им была получена зависимость вероятности попадания получаемого результата в определённый интервал то числа измерений. Однако эта зависимость имеет сложный характер и не выражается через элементарные функции.

На основе распределения Стьюдента были составлены таблицы коэффициентов Стьюдента 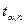, которые показывают во сколько раз нужно увеличить величину 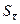, чтобы при определённом числе измерений n получить задаваемую вероятность (надёжность) 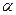. Коэффициенты Стьюдента представлены в Таблице 1 Приложения.

В результате можно записать:

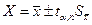(10.1)

где 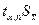- доверительный интервал, который означает, что истинное значение измеряемой величины находится в интервале 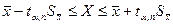с вероятностью или надёжностью 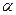, где

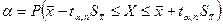. (10.2)

Дата добавления: 2015-07-13