Стандартное отклонение среднего

ПРЯМЫЕ ИЗМЕРЕНИЯ

В реальных условиях число измерений конечно. Если, например, сделано N измерений величины x (то есть некоторый эксперимент независимо повторён N раз), то полученные результаты называют случайной выборкой объёма N из множества всех возможных значений величины x.

В теории обработки результатов (см.п.2.2) эксперимента строго доказывается, что в этом случае наилучшей оценкой истинного значения X является выборочное среднее значение из N измерений:

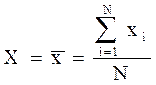(6.1)

Кроме того, наилучшей оценкой стандартного отклонения является выборочное среднее квадратичное отклонение :

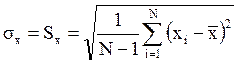(6.2)

Предположим, что результаты измерений величины x распределены нормально около истинного значения X с шириной . Необходимо узнать, какова надёжность среднего значения для N измерений. Для ответа на этот вопрос представим себе, что N измерений повторяются много раз, причём в каждом случае определяется среднее значение 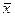. Нас интересует, как распределены полученные значения .

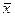Величина 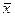есть простая функция измеренных значений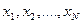

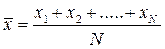(7.1)

Поэтому можно найти распределение 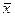с помощью расчёта ошибок для косвенных измерений.

Поскольку каждое из измеренных значений 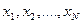распределено нормально, то очевидно, что и 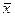также имеют нормальное распределение. Так как истинным значением для 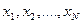является X, то и истинным значением 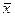является также X. Следовательно, полученные значения 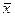распределены нормально около истинного значения X. Ширину этого распределения можно найти по формуле:

(7.2)

Но:

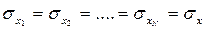(7.3)

а из (7.1) следует:

. (7.4)

Следовательно, вместо (7.2) получаем:

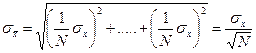(7.5)

Эту величину называют стандартным отклонением среднего. Видно, что при 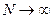значение .

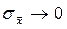Вывод: значения 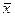распределены нормально с центром, равным истинному значению и с шириной 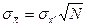; другими словами, если найдено однажды 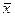, то вероятность попадания этого значения в интервал равна 68%.

Для оценки стандартного отклонения среднего, которую обозначим 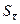, используют формулу

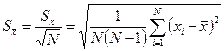(7.6)

Величину 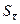называют выборочным стандартным отклонением среднего. Видно, что при увеличении числа измерений N растёт точность измерения. Стандартное отклонение среднего при косвенных измерениях может быть определено по формуле:

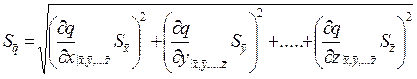(7.7)

Пример: определим выражение для стандартного отклонения величины q, которая связана с величинами x,y,z, определяемыми прямыми измерениями, следующим соотношением:

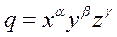, (7.8)

где - точные числа.

Для частных производных получаем:

. (7.9)

После подстановки (7.9) в (7.7) имеем:

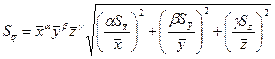(7.10)

Дата добавления: 2015-07-13