
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Введение. Одним из важнейших факторов научно-технического прогресса, способствующих скорейшему совершенствованию общественного производства и росту его эффективности
|
|
|
|
Одним из важнейших факторов научно-технического прогресса, способствующих скорейшему совершенствованию общественного производства и росту его эффективности, является проблема повышения уровня подготовки специалистов.
Решению этой задачи способствует выполнение курсового проекта по «Деталям машин», базирующегося на знаниях физико-математических и общетехнических дисциплин: математики, механики, сопротивления материалов, технологии металлов, черчения.
Объектом курсового проектирования является одноступенчатый редуктор-механизм, состоящий из зубчатой передачи, выполненный в виде отдельного агрегата и служащий для передачи вращения от вала двигателя к валу рабочей машины.
Назначение редуктора - понижение угловой скорости и соответственно повышение вращающего момента ведомого вала по сравнению с ведущим валом.
Редуктор проектируется по заданной нагрузке (моменту на выходном валу) и передаточному числу без указания конкретного назначения, что характерно для специализированных заводов, на которых организовано серийное производство редукторов
1.Выбор электродвигателя и кинематический расчёт
1.1 Составляем кинематическую схему
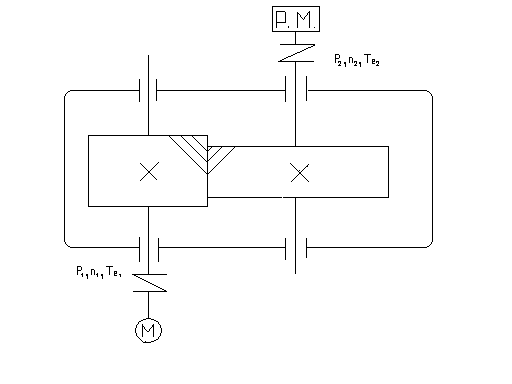
1.2 Определяем общий КПД редуктора
η = η3 · ηп2
где η3 –КПД пары зубчатых цилиндрических косозубых колёс;
η3=0,98;
ηп –КПД, учитывающий потери в одной паре подшипников качения;
ηп =0,99;
η =0,97·0,992= 0,96
1.3 Определяем мощность на ведущем валу
η =Р2/ Р1
Р1= Р2· η
Р1=5,5 кВт
1.4 Определяем частоту вращения ведомого вала
U=n1/n2
n2 = n1/ U
n1=2.8·341=954,8 мин-1
1.5 Подбираем электродвигатель по исходным данным, поскольку вал двигателя соединяется с быстроходным валом редуктора муфтой.
Р1=55 кВт;
n1=965 мин-1.
Примечание: при подборе мощности двигателя допускается его перегрузка до 5…8% при постоянной нагрузке и до 10…12% при переменной нагрузке [2,с.5]; отклонение частоты вращения вала двигателя от заданной допускается+3%[5,с.8].
Выбираем электродвигатель с номинальной мощностью равной или несколько превышающей Р1 и с угловой скоростью близкой к n1. Принимаем электродвигатель единой серии 4А тип 132S6/965, для которого:
Рдв=55кВт;
nдв=965 мин-1;
dдв=38 мм.
Окончательно принимаем:
Р1=5.5 кВт; n1 =954.8 мин-1.
1.6 Проверяем отклонение частоты вращения вала двигателя от заданной для быстроходного вала редуктора
(nдв – n1)/nдв· 100%
(965-954.8)/965·100%= 1.05%
Принимаем n1=965мин-1.
1.7 Определяем мощность на ведомом валу:
Р2 =Р1·η
Р2 = 5.5·0.96=5.28 кВт
1.8 Уточняем частоту вращения ведомого вала редуктора
U= n1/n2
n2 = n1/U
n2 = 965/2.8=344.6 мин-1
1.9 Определяем вращающие моменты на ведущем и ведомом валах Те1 и Те2
Те1=9,55 · Р1/ n1
Те1= 9,55·5.5·10³/965 =54.4 Нм
Те2=Те1·U·η
Те2= 54.4·8.2·0.96=146.2 Нм
1.10 Задаём число зубьев шестерни Z1, с целью уменьшения шума принимаем Z1≥25[4,с.314].
Принимаем Z1=26
1.11 Определяем число зубьев колеса Z2:
U= Z2/Z1
Z2 = U · Z1
Z2 = 2.8·30=84
1.12 Задаёмся предварительно углом наклона зуба согласно рекомендации β =8º -20º для косозубых передач.
Принимаем β=10º.
2 Расчёт зубчатой передачи
2.1 Выбор материалов и определение допускаемых напряжений
2.1.1 Поскольку в проектном задании к редуктору не предъявляется жёстких требований в отношении габаритов передачи, а изготовление колёс осуществляется в условиях мелкосерийного производства, то выбираем материалы со средними механическими свойствами. С целью сокращения номенклатуры применяемых материалов принимаем для шестерни и колеса сталь 45, так как передаваемая валом мощность невелика и для достижения лучшей приработки твёрдость колёс должна быть не более 350НВ. Кроме того, редуктор должен быть общего назначения, а для таких редукторов экономически целесообразно применять колёса с твёрдостью меньшей или равной 350НВ. Учитывая, что число нагружений в единицу времени зубьев шестерни в передаточное число раз больше числа нагружений зубьев колеса, для обеспечения одинаковой контактной усталости, механические характеристики материала шестерни должны быть выше, чем у колеса.
НВ1= НВ2 + (20…70) [6,с.48]
Чтобы этого достичь при одинаковых материалах, назначаем соответствующий режим термообработки, полагая, что диаметр заготовки шестерни не превысит 100мм, о колеса 300мм.
Шестерня: сталь 45, термообработка – улучшение
Принимаем: НВ1 = 210; σу= 290 МПа; σu= 730 МПа[5,с.34].
Колесо: сталь 45; термообработка – нормализация
Принимаем: НВ2 =190; σу= 290 МПа; σu=170 МПа[5,с.34].
НВ1 – НВ2 = 210 -190= 20
что соответствует указанной рекомендации.
2.1.2 Определяем допускаемые контактные напряжения при расчете на контактную усталость
σнр =((σнlim b· ZN)/SH)· ZR· ZV· ZL· ZX [1,с.14]
где σнlimb –предел контактной выносливости поверхности зубьев, соответствующий базовому числу циклов напряжений.
σнlimb = 2 · НВ + 70 [1,с.27],[5,c.34]
σн limb1 = 2 · 210 + 70 = 490МПа
σн limb2 = 2 · 190 + 70= 450МПа
ZN –коэффициент долговечности, учитывающий срок службы передачи. Поскольку в проектном задании указано, что редуктор предназначен для длительной работы, то есть число циклов NN больше базового No, то ZN=1[1,c.24],[5,с.33];
ZR –коэффициент, учитывающий шероховатость сопряженных поверхностей зубьев[1, c.25];
ZV –коэффициент, учитывающий влияние окружной скорости;
ZL –коэффициент, учитывающий влияние вязкости смазочного материала;
ZX –коэффициент, учитывающий размер зубчатого колеса.
ГОСТ 21357-87 рекомендует для колес d‹1000 мм принимать
ZR · ZV · ZL · ZX = 0,9 [1,с.57]
SH –коэффициент запаса прочности.
Для нормализованных и улучшенных сталей SН=1,1[1,с.24].
σнр1= 401МПа
σнр2=360МПа
В качестве расчётного значения для косозубых передач принимаем:
σнр = 0,45 · (σнр1+σнр2) ≥ σнрmin [1,c.19]
σнр = 0,45 · (401+368)= 346MПа
Проверяем соблюдение условия
σнр < 1,23 σнрmin [1,c.19]
1,23·368 = 453МПа > σнр
Принимаем σнр = 368МПа.
2.1.3 Определяем допускаемые напряжения изгиба при расчёте на усталость
σFP = σFlim b· YN /SFmin· YR · YX · Yδ [1,с.5]
где σFlimb –предел выносливости зубьев при изгибе, соответствующий базовому числу циклов напряжений.
σFlimb = 1,8 · НВ [5,с.45]
σFlimb1 = 1,8 · 210 = 378МПа
σFlimb2 = 1,8 · 190 = 342МПа
SFmin –минимальный коэффициент запаса прочности;
SFmin = 1,7[1,с.35].
Принимаем SFmin = 1,7
YN –коэффициент долговечности, зависящий от соотношения базового и эквивалентного циклов;
YN =1[5,с.45];
YR –коэффициент, учитывающий влияние шероховатости переходной поверхности, он отличен от 1 лишь в случае полирования переходной поверхности;
YR =1[5,с.46];
YX –коэффициент, учитывающий размеры зубчатого колеса;
При dа≤300мм YX=1[5,с.46];
Yδ –опорный коэффициент, учитывающий чувствительность материала концентрации напряжений;
Yδ=1[1,с.124].
σFP1 = 378·1/1,7·1·1·1 = 222МПа
σFP2 =342·1/1,7·1·1·1 = 201МПа
2.2 Проектировочный расчёт передачи на контактную усталость активных поверхностей зубьев
2.2.1 Определяем ориентировочное значение делительного диаметра шестерни
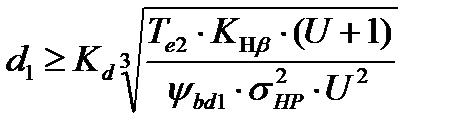 [1,с.57]
[1,с.57]
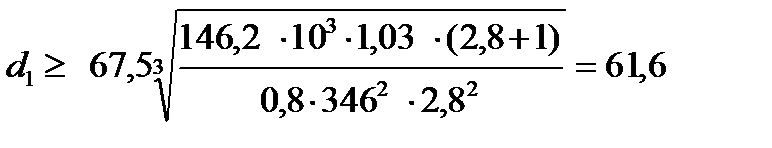
где Кd –вспомогательный коэффициент;
Кd=67,5МПа1/3 для косозубых и шевронных передач [1,с.57];
Ψвd1 –коэффициент ширины шестерни относительно её диаметра.
Принимаем Ψвd1=0,8 при симметричном расположении колёс;
Кнβ -коэффициент неравномерности распределения нагрузки по ширине венца. Выбираем по графику в зависимости от твёрдости рабочих поверхностей зубьев, схемы нагружения и параметра Ψвd1[1,с.58];
Кнβ =1,03
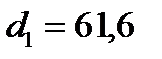 мм
мм
Принимаем d1= 61,6 мм.
2.2.2 Определяем делительный диаметр колеса d2
U = d2/d1
d2 = U · d1
d2 = 2,8 =61,6 мм
Принимаем d2=172,48 мм.
2.2.3 Определяем межосевое расстояние передачи
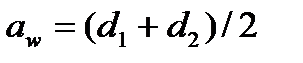 [5,c.37]
[5,c.37]
aw=(172,48+61,6)/2=117,04 мм
Принимаем aw= 125 мм по ГОСТ 2185-66.
2.2.4 Определяем рабочую ширину колёс b1 и b2. Учитывая неточность сборки и возможную осевую «игру» передачи выбираем
b1= b2 + 5мм
b1= Ψвd1 · d1
b1= 0,8· 61,6 =50 мм
Принимаем b1=50 мм(Ra20).
b2= b1 – 5мм
b2= 50-5=45 мм
2.2.5 Определяем нормальный модуль по эмпирической зависимости
mn = 0,02 · aw [5,c.293]
mn =0,02· 125 = 2,5 мм
Принимаем mn= 2,5мм.
Определяем суммарное число зубьев
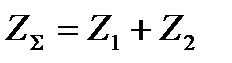
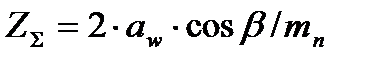 [5,c.36]
[5,c.36]
ZΣ=2· 125·0.98/2.5=98
Принимаем ZΣ=98
Определяем числа зубьев шестерни и колеса
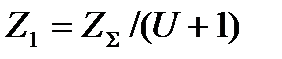 [5,c.37]
[5,c.37]
Z1=98/(2,8+1) =26
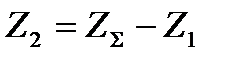
Z2 = 98 - 26=72
По округлённым значениям Z1 и Z2 уточняем передаточное число
Uп= Z2 / Z1 [5,c.37]
Uп=72/26=2,76
Проверяем отклонение передаточного числа от заданного значения
(Uз – Uп)/ Uз · 100%
(2,8-2,76)/2,8· 100% =1.4%
Действительное значение угла наклона линии зуба β
cosβ= 0,5 · (Z1 + Z2) · mn/ aw
cosβ= 0,5 · (26+72) ·2,5/125=0,98
β=11°
2.2.6 Определяем окружной модуль
mt = mn/ cosβ [3,c.142]
mt = 2.5/0.98=2.55мм
2.2.7 Уточняем диаметры делительных окружностей и межосевое расстояние
d1= mt · Z1
d1= 2.5·26=66.3мм
d2= mt · Z2
d2 = 2.55·72 =183.6мм
aw =(d1+d2)/ 2
aw= (66.3+183.6)/2 =124.95мм
2.3 Проверочные расчёты передачи
2.3.1 Проверочный расчёт передачи на контактную усталость активных поверхностей зубьев выполняем по условию контактной прочности
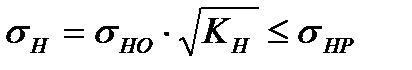
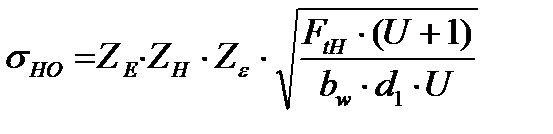
где ZЕ –коэффициент, учитывающий механические свойства сопряженных зубчатых колес;
ZЕ=190[1,с.113];
ZН –коэффициент, учитывающий форму сопряженных поверхностей зубьев в зацеплении;
ZН=2,41[1,с.113];
Zε –коэффициент, учитывающий суммарную длину контактных линий;
При εβ≥1
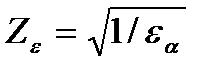 [1,с.15]
[1,с.15]
εα = [1,88 - 3,2 · (1/ Z1 + 1/ Z2)] · cosβ [5,с.39]
εα =[1,88 - 3,2 · (1/26 + 1/72)] ·0.98 = 1.7
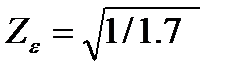 =0.77
=0.77
FtH –исходная окружная сила
FtH = 2 · Te1/d1
FtH = 2 · 54.4 · 102/ = 1776Н
Коэффициент нагрузки Кн определяется по следующей зависимости
Кн = КА· КHv· KHβ· KHα [1,с.14]
где КА –коэффициент, учитывающий внешнюю динамическую нагрузку;
КА = 1[1,с.15];
КHv –коэффициент, учитывающий динамическую нагрузку, возникающую в зацеплении до зоны резонанса;
V = 0,1· nдв· d1/ 2000
V = 0,1·965·61.6/2000 = 2.97м/с
При такой скорости следует принять 8 степень точности и тогда:
КHv= 1[5,с.40];
KHβ –коэффициент, учитывающий неравномерность распределения нагрузки между зубьями;
KHβ= 1,03[5,с.39];[1,с.58];
KHα –коэффициент, учитывающий распределение нагрузки между зубьями;
KHα = 1,09[5,с.39];
КН =1·1·1.03·1.08 =1.11
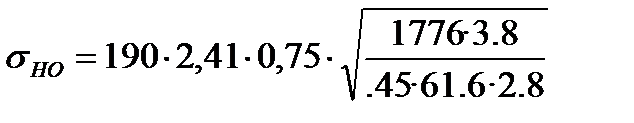 =319МПа
=319МПа
Подставляем все вычисленные значения в формулу для проверочного расчёта
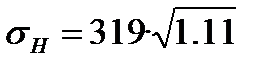 = 351 МПа
= 351 МПа
Определяем процент недогрузки
(σн – σнр)/ σнр · 100%
(346-351)/351·100% = -1.4%
что соответствует рекомендации.
2.3.2 Проверочный расчёт на усталость по напряжениям изгиба выполняем по условию прочности
σF ≤ σFP [1,с.29]
Расчётное местное напряжение при изгибе определяем по формуле:
σF = KF · YFS · Yβ · Yε · FtF /(в · m) [1,с.29]
Для коэффициента нагрузки КF принимают:
КF = КА · КFv · KFβ · KFα [1,с.29]
где КА –коэффициент, учитывающий внешнюю динамическую нагрузку;
КА=1[1,с.29];
КFv –коэффициент, учитывающий динамическую нагрузку, возникающую в зацеплении до зоны резонанса;
КFv =1,3[5,с.43];
KFβ –коэффициент, учитывающий неравномерность распределения нагрузки по длине контактных линий;
KFβ=1,08[1,с.59];
KFα –коэффициент, учитывающий распределение нагрузки между зубьями.
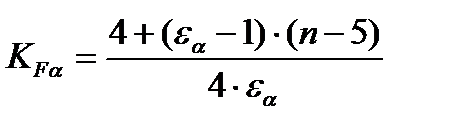 [5,с.295]
[5,с.295]
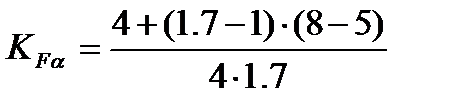 =0.9
=0.9
KF =1·1.9·1.08·0.9=1.26
YFS –коэффициент, учитывающий форму зуба и концентрацию напряжений, определяется в зависимости от эквивалентного числа зубьев
Zv1 = Z1 / cos3β [1,с.62]
Zv1= 26/0.983=27.6
при этом YFs1 =3.8 [1,с.38],[5,с.42].
Zv2 = Z2 /cos3β
Zv2 = 72/0.94 =76.6
при этом YFs2=3.61 [1,с.38],[5,с.42].
Так как шестерня и колесо выполнены из одинаковых материалов, то расчёт ведём по тому из колёс, для которого YFS больше, то есть по шестерне.
Принимаем YFS =3.8
Yε –коэффициент, учитывающий перекрытие зубьев:
Yε =1/ εα [1,с.32]
Yε = 1/1.7=0.59
Yβ – коэффициент, учитывающий наклон зуба.
Уβ = 1- εβ · β / 120
εβ = b2 / Рх
Px= Pn / sinβ
Pn= mn· π
Pn=2.5·3,14=7.85мм
Px= 7.85/0.19= 41.3мм
εβ = 45/41.3=1.09
Уβ = 1-1.09·11/120=0.9
Подставляем все значения в формулу для проверочного расчёта передачи:
σF= 1.26·3.80·0.9·0.59·1766/(50·2.5)=36МПа
Напряжение изгиба σF значительно ниже допускаемого напряжения σFР, но это нельзя рассматривать как недогрузку передачи, поскольку основным критерием её работоспособности является контактная усталость.
2.4 Определение геометрических параметров колёс
2.4.1 Высота головки зуба
ha = mn
ha = 2.5мм
2.4.2 Высота ножки зуба
hf = 1,25 · mn
hf= 1,25·2.5= 3.1мм
2.4.3 Диаметры вершин зубьев
da1 = d1 + 2 · ha
da1 = 61.6+2·2.5 = 66.6мм
da2 = d2 + 2 · ha
da2 = 172.48+2·2.5 = 177.48мм
2.4.4 Диаметры впадин зубьев
df1 = d1 - 2 · hf
df1 = 61.6-2·3.1 = 55.4мм
df2 = d2 - 2 · hf
df2 =172.48-2·3.1 =166.28мм
2.5 Определение сил, действующих в зацеплении
2.5.1 Окружная сила
FtH = 2 · (Te1/d1) · 10³
FtH = 2·(54.4/61.6) · 103= 1766H
2.5.2 Радиальная сила
Fr = Ft · tgα / cosβ
α=20º
Fr=1766·0.36/0.98=649H
2.5.3 Осевая сила
Fa= Ft · tgβ
Fa= 1766·0.19 =335.5H
3 Предварительный расчёт валов редуктора
3.1 Вал редуктора испытывает совместное действие изгиба и кручения, причём характер изменения напряжений – повторно-переменный, поэтому основным расчётом валов является расчёт на выносливость, но в начале расчёта известны только крутящий момент Т, который численно равен передаваемому вращающему моменту Те. Изгибающие моменты Ми оказывается возможным определить лишь после разработки конструкций вала, когда, согласно чертежу, выявляется его длина. Кроме того, только после разработки конструкции определяются места концентрации напряжений: галтели, шпоночные канавки и т.д.
Поэтому, прежде надо сделать предварительный расчёт валов, цель которого – определить диаметры выходных концов валов.
Расчёт проводим условно только на кручение, исходя из условия прочности при кручении
τ ≤ τadm
где τadm – допускаемое напряжение на кручение.
Поскольку мы заведомо пренебрегаем влиянием изгиба и концентрацией напряжений, то эту ошибку компенсируем понижением допускаемых напряжений.
Выбираем материал для валов: ведущий вал – сталь40Х; ведомый вал – сталь45, для которого τadm =25МПа.
τ –касательное напряжение, возникающее в расчётном сечении вала.
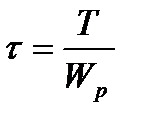
где Т –крутящий момент.
Ведущий вал: Тe1=…Н·мм; ведомый вал: Те2=…Н·мм.
Wр –полярный момент сопротивления сечения при кручении.
Wр= 0,2 · dв³
Подставляем значения в условие прочности, получим ведущий вал:
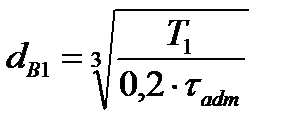
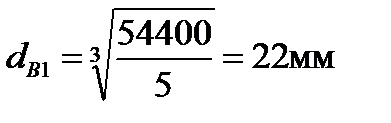
Полученный результат округляем по ГОСТ 6636 – 69 до ближайшего большего значения из ряда R40[5,с.161].
Принимаем dв1=22мм.
Ведущий вал редуктора соединяем с валом двигателя, чтобы выполнялось соотношение dв1/dдв ≤ 0,75.
dдв= 38мм
dв1 = 0,75 · 38= 28.5мм
Принимаем dв1= …мм, согласуя с ГОСТ 6636 – 69[5,с.161].
Ведомый вал:
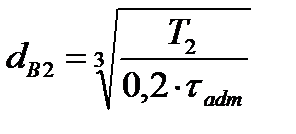
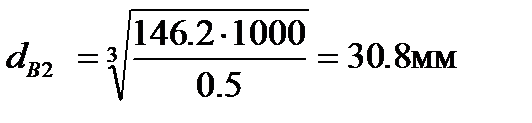
Полученный результат округляем по ГОСТ 6636 – 69 до ближайшего большего значения из ряда R40[5,с.161].
Принимаем dв2 = 31мм.
3.2 Основные нагрузки, действующие на валы, возникают в зубчатом зацеплении:
Fa=335,5H;
Fr=649H;
Ft=1766H.
Собственный вес вала и насаженных на нем деталей не учитываем, поскольку они играют роль лишь в весьма мощных передачах, где сила тяжести деталей выражаются величиной того же порядка, что и силы в зацеплении.
Силы трения в опорах не учитываются. Большинство муфт, вследствие неизбежной несоосности соединяемых валов, нагружают вал дополнительной силой Fм.
При расчёте валов можно приблизительно считать
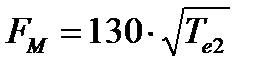
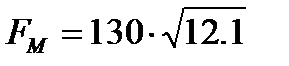 = 451,1Н
= 451,1Н
где вращающий момент Те2=Т2.
На тихоходном валу редуктора, где вращающий момент значителен, должна быть предусмотрена расчетная консольная нагрузка Fм, приложенная к середине выступающего конца вала.
Направление силы Fм в отношении окружной силы Ft может быть любым, так как это зависит от случайных неточностей монтажа.
Поэтому в расчётных схемах силу Fм направляем так, чтобы она увеличивала напряжение от окружной силы Ft (худший случай).
На расчётных схемах все силы, действующие на вал, а так же вращающие моменты как сосредоточенные, приложенные к середине ступиц, хотя в действительности они распределены по длине ступицы.
3.3 Диаметры под подшипники и колесо.
3.3.1 Ведущий вал:
Диаметр под подшипники
dn1 = dв1 + 2 · t
где t=2мм[6,с.108].
dn1 = 22+2·2= 24мм.
Принимаем dn1= 24мм.
3.3.2 Ведомый вал:
Диаметр под подшипники
dn2 = dв2 + 2 · t
где t=2мм[6,с.108].
dn2 =31+2·2= 35мм
Принимаем dn2 =35мм.
Посадочный диаметр под колесо:
dk2 = dn2 + 3,2 · r
где r –радиус галтели;
r=2мм[6,с.108].
dk2 =35+6,4=41,4мм
Принимаем dк2=41,4мм.
|
|
|
|
|
Дата добавления: 2015-07-13; Просмотров: 377; Нарушение авторских прав?; Мы поможем в написании вашей работы!