Тема 2. Статистическая обработка данных для моделирования

Целью статистической обработки исходных данных для математического моделирования является оценка их однородности (принадлежности к одной статистической совокупности), вариабельности (изменчивости) и надежности.

Для проведения вычислений может быть использован MS Excel. Это широко распространенное приложение имеет в своем составе надстройку «Пакет анализа» – дополнительный компонент программы, включающий набор математических методов обработки и графического представления данных. Доступ к нему осуществляется в MS Excel 2000-2003 через меню «Сервис» - «Анализ данных», в MS Excel 2007 - через меню "Данные".

Доступ к пакету анализа в MS Excel 2000-2003

Доступ к пакету анализа в MS Excel 2007

Статистическую обработку массива исходных данных можно выполнить с использованием двух функций: «Гистограмма» и «Описательная статистика».

Оценка однородности выборки

Функцию «Гистограмма» следует применять для оценки однородности больших выборок (n > 30).

Если гистограмма распределения данных имеет один пик, то выборку считают однородной и анализируют целиком (рис. 1). В том случае, когда на гистограмме выделяется два или более пика, выборка является неоднородной, то есть состоит из двух или более соединенных массивов данных (рис.2). Например, в выборку данных о содержании гумуса в почвах могут попасть данные по двум разным почвам. При достаточно большом количестве данных они распределятся в выборке неравномерно и дадут на гистограмме два пика. Очевидно, что анализ такой выборки целиком будет грубой ошибкой. Поэтому она должна быть разделена на две части, каждую из которых следует анализировать отдельно.

В качестве примера рассмотрим оценку однородности и надежности данных выборки по содержанию гумуса в почве.

Содержание гумуса в черноземе, %

6,20	6,05	6,40	6,29	6,15	6,00	6,16	6,21	6,25	6,25
6,26	6,05	6,03	6,02	6,24	6,13	6,20	6,29	6,23	6,23
6,20	6,45	6,42	6,36	6,31	6,30	6,35	6,30	6,21	6,01
6,35	6,20	6,30	6,32	6,40	6,30	6,26	6,19	6,26	6,16
6,16	6,14	6,13	5,95	5,96	6,04	6,01	6,28	6,16	6,21

Для установления однородности выборки введем все данные в один столбец таблицы MS Excel. Порядок введения данных значения не имеет. Для упрощения этой работы можно скопировать данные задания в буфер обмена и вставить в таблицу Excel. О дальнейших действиях смотрите видеопример.

Запускаем функцию «Гистограмма». Указываем входной интервал данных, обведя их мышью при нажатой левой клавише. Затем ставим метку у пункта «Вывод графика». Выполнив эти действия, получаем на новом рабочем листе гистограмму:

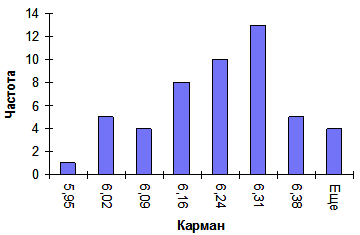
Рис. 1. Пример гистограммы однородной выборки

По данной гистограмме можно сделать вывод, что выборка вполне однородна, так как на гистограмме присутствует только один четко выделяющийся пик. Поэтому выборку можно анализировать целиком.

Несимметричность гистограммы и невыровненность, в том числе спад в третьем столбце, объясняются недостаточным количеством исходных данных.

На рисунке 2 приведен пример гистограммы неоднородной выборки.

Рис. 2. Пример гистограммы неоднородной выборки

На ней видны два четких пика, в соответствии с которыми гистограмма может быть разделена на две части (показано пунктирной линией). Данные этих частей фактически представляют собой две различные выборки, которые при получении исходной информации ошибочно были объединены. Если причина подобного распределения данных неизвестна, то использовать их для моделирования нецелесообразно.

Вычисление основных статистических характеристик выборки

Так как анализируемая выборка оказалась однородной выполним вычисление основных статистических характеристик, которые позволят дать оценку качества исходных данных и их пригодности для моделирования. Воспользуемся для этого функцией «Описательная статистика». В одноименном диалоговом окне указываем входной интервал данных и ставим отметку у пункта «Итоговая статистика».

После вычисления на новом рабочем листе получаем результат:

Среднее	6.2066
Стандартная ошибка	0.017549
Медиана	6.21
Мода	6.2
Стандартное отклонение	0.12409
Дисперсия выборки	0.015398
Эксцесс	-0.50347
Асимметричность	-0.28736
Интервал	0.5
Минимум	5.95
Максимум	6.45
Сумма	310.33
Счет

Данная таблица результатов статистического анализа содержит показатели, характеризующие распределение данных в выборке (медиана, мода, эксцесс, асимметричность) и ряд величин, которые можно использовать для вычисления важнейших статистических характеристик.

Для того, чтобы дать оценку изменчивости данных выборки необходимо вычислить коэффициент вариации:

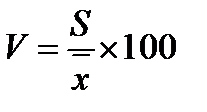
где S – стандартное отклонение.

Расчет по данной формуле может быть выполнен в MS Excel. Ставим курсор в ячейку, выбранную для размещения коэффициента вариации, и нажимаем на клавиатуре «=». Затем мышью кликаем на величину стандартного отклонения и на клавиатуре нажимаем «/» (разделить). После этого мышью кликаем на величину среднего и с помощью клавиатуры дописываем «*100», что означает «умножить на 100». Нажав клавишу «Enter», в заданной ячейке получаем величину коэффициента вариации.

Коэффициент вариации величина относительная и измеряется в процентах. Обычно пользуются следующей градацией коэффициента вариации: < 10 % – изменчивость слабая; 10-20 % – изменчивость средняя; > 20 % – изменчивость сильная.

В рассматриваемом примере коэффициент вариации равен 2%, что указывает на очень слабую изменчивость данных в выборке.

Следует помнить, что величинам, различным по своей природе, может быть свойственна и различная изменчивость, поэтому данная шкала является лишь ориентировочной. По этой же причине сильная изменчивость данных выборки не является однозначным признаком их ненадежности, а слабая изменчивость не может гарантировать их надежности.

Более объективно о надежности данных можно судить по достоверности среднего. Для установления достоверности среднего используют критерий достоверности Стьюдента t. Он равен отношению среднего (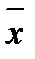) к величине его абсолютной ошибки ():

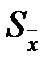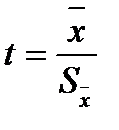
где 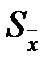– ошибка выборочного среднего абсолютная (стандартная ошибка в MS Excel).

Фактическое значение t, вычисленное по данным рассматриваемого примера, равно:

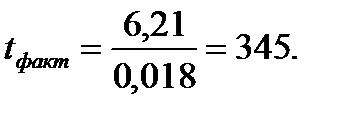
Для установления достоверности среднего вычисленное значение критерия Стьюдента сравнивают с его теоретическим значением, которое находят в таблице 2. Предварительно вычисляют число степеней свободы n (ню). Для одной выборки число степеней свободы будет равно:

n = n – 1,

где n – количество данных в выборке.

Для рассматриваемого примера число степеней свободы равно:

n = 50 – 1 = 49.

В столбце «Число степеней свободы» таблицы 2 находим соответствующую строку. Справа от этого столбца расположены столбцы со значениями критерия t при разных уровнях вероятности. Для большинства задач используют уровень вероятности 0,95. Это означает, что точность осуществляемой оценки составляет 95%. Значение t_теор из столбца с уровнем вероятности 0,95 равно 2,01.

Вывод: t_факт = 345 > t_теор = 2,01, следовательно, величина выборочного среднего является достоверной.

Таблица 2. Стандартные значения критерия t (Стьюдента)

Число степеней свободы, n	Уровень вероятности (значимости)	Число степеней свободы, n	Уровень вероятности (значимости)
0,95 (0,05)	0,99 (0,01)	0,999 (0,001)	0,95 (0,05)	0,99 (0,01)	0,999 (0,001)
1	12,71	63,66	637,0	13	2,16	3,01	4,22
2	4,30	9,93	31,60	14-15	2,14	2,97	4,10
3	3,18	5,84	12,94	16-17	2,12	2,91	4,00
4	2,78	4,60	8,61	18-20	2,10	2,86	3,88
5	2,57	4,03	6,86	21-24	2,07	2,83	3,77
6	2,45	3,71	5,96	25-28	2,05	2,78	3,70
7	2,37	3,50	5,41	29-30	2,04	2,76	3,66
8	2,31	3,36	5,04	31-34	2,03	2,74	3,64
9	2,26	3,25	4,78	35-42	2,02	2,71	3,59
10	2,23	3,17	4,59	43-62	2,01	2,68	3,50
11	2,20	3,11	4,44	63-175	1,98	2,63	3,39
12	2,18	3,06	4,32	176 и более	1,96	2,58	3,29

Для оценки точности данных целесообразно вычислить относительную ошибку выборочной средней ():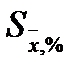

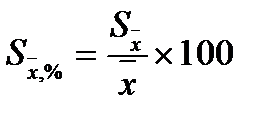
Относительная ошибка для рассматриваемого примера:

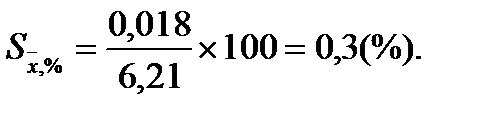
Для оценки точности данных по величине 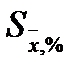пользуются следующей шкалой: < 3% – точность высокая; 3-7% – точность средняя; > 7% – точность низкая.

Обратите внимание! На ненадежность данных указывает не только большая ошибка, но и слишком маленькая (доли процента). Для данных, характеризующих климат, сложные и биологические объекты, величина ошибки в пределах нескольких десятых долей процента указывает скорее на недобросовестность работника или на измерительные, вычислительные и иные ошибки, чем на действительно очень высокую точность. Поэтому такие данные следует признавать ненадежными.

Вычисленное нами значение 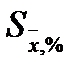= 0,3% очень мало. С учетом того, что выборка содержит данные, характеризующие очень сложный природный объект – почву, мы должны признать, что, несмотря на все предыдущие выводы о надежности информации, она все же является ненадежной. В действительности, исходные числа рассмотренного примера не являются реальными данными о содержании гумуса в почве. Они вымышлены, что и позволила выявить статистическая обработка.

Таким образом, окончательный вывод – данные ненадежны и не могут быть использованы для математического моделирования.

Задание 2. Оцените однородность данных выборки, выполните их статистическую обработку в выше приведенной последовательности и сделайте вывод об их качестве:

2.1.

2.2.

30,5	28,5	36,5	37,0	38,8	32,4	42,2	37,7	40,2	32,0
38,5	36,5	36,9	37,1	38,1	40,0	39,9	40,1	39,1	40,4
37,0	34,6	39,7	34,6	36,9	39,8	31,0	39,2	36,8	37,2
40,5	37,1	36,7	31,5	34,7	38,7	38,8	38,9	42,2	42,4
38,9	39,5	34,6	38,9	36,8	38,4	37,9	42,3	37,1	44,4

2.3.

2.4.

3,0	3,2	3,4	3,2	3,0	3,1	3,2	3,2	3,4	3,3
3,8	3,5	3,6	3,4	3,8	3,5	4,1	3,1	3,5	3,2
3,1	3,2	3,8	3,0	3,2	3,6	3,5	3,8	3,1	3,4
3,8	3,3	3,6	3,8	3,9	3,6	3,7	3,5	3,2	4,0
4,1	3,4	3,7	3,9	3,2	3,3	2,9	2,6	2,5	4,3

2.5.

2.6.

2.7.

31,5	27,8	28,3	30,2	30,8	30,5	29,7	31,0	33,8
30,2	31,0	28,9	31,2	28,5	30,7	30,7	30,5	29,5
29,8	32,2	31,7	32,1	31,3	30,2	31,4	30,8	30,3
29,3	32,7	29,9	29,4	30,9	29,4	31,6	29,1	29,9

2.8.

2.9.

2.10.

22,9	22,4	20,6	21,9	20,3	19,4	23,9	22,1
22,8	22,1	21,3	20,6	21,4	19,5	25,1	22,5
22,1	10,8	22,0	20,5	32,6	22,5	24,2	21,8
21,6	23,3	21,3	21,3	21,7	23,3	22,0	23,4
19,9	21,7	21,0	20,2	19,0	24,2	24,2	21,6

2.11.

9,22	11,02	13,86	3,05	6,61	4,18	11,16	6,72
9,83	23,19	14,55	3,62	7,58	4,78	5,55	7,35
10,37	5,43	17,08	3,62	4,64	7,65	5,59	7,60
10,45	3,08	4,85	10,31	3,04	3,08	4,88	8,02
10,80	6,27	9,68	1,80	4,16	19,26	6,21	8,51

2.12.

Дата добавления: 2015-08-31