Тема 4. Корреляционный и регрессионный анализ данных

Выполняя анализ данных и подготавливая их для математического моделирования часто возникает потребность в выявлении зависимостей между рассматриваемыми величинами.

Основным методом, позволяющим оценить тесноту и направление связи, является корреляционный анализ. Чаще всего используют частную (парную) корреляцию при линейной форме связи.

Для того, чтобы выполнить корреляционный анализ необходимо иметь сопряженные (парные) данные. Например, данные о содержании гумуса в почве полей и урожайность по этим же полям.

Выполнить корреляционный анализ легко с помощью MS Excel. В «Пакете анализа» этого приложения есть функция «Корреляция», вычисляющая коэффициент парной линейной корреляции r (Пирсона).

Например, нужно выявить направление и тесноту связи между содержанием гумуса в почвах и их бонитетом:

Гумус, % 5,1 4,6 7,0 5,4 5,0 6,5 6,1 6,8 4,9 5,2 5,6

Балл 47 40 61 49 45 54 53 56 48 50 54

Вводим данные в таблицу MS Excel в два соседних столбца и запускаем функцию «Корреляция». В диалоговом окне функции указываем входной интервал: выделяем сразу оба столбца. Результат расчетов по умолчанию будет выведен на новый рабочий лист:

	Строка 1	Строка 2
Строка 1
Строка 2	0.917966

Для вывода результата на текущий лист нужно задать выходной интервал.

Таблица результатов всегда будет иметь такой вид. Изменяться будет только значение коэффициента корреляции r, выделенное жирным шрифтом.

Величину коэффициента корреляции, как правило, округляют до десятых.

О направлении связи судят по знаку коэффициента корреляции. Минус указывает на обратную связь, а плюс (обычно опускается при написании) – на прямую.

Вывод о тесноте связи делают по величине модуля коэффициента корреляции. При этом, как правило, пользуются следующей шкалой:

0,0 – связь отсутствует;

< 0,3 – связь слабая;

0,3-0,7 – связь средняя;

> 0,7 – связь сильная;

1,0 – связь полная (функциональная).

Полученное в результате расчета значение коэффициента корреляции (r» 0,9) указывает на сильную прямую связь.

Значение коэффициента корреляции при низком качестве данных может быть статистически недостоверным. Для установления его достоверности используют критерий достоверности Стьюдента t, который в этом случае рассчитывается как отношение модуля коэффициента корреляции r к величине его ошибки S_r:

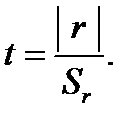
Ошибка коэффициента корреляции вычисляется по следующей формуле:

После вычисления t_факт по таблице 2 находят t_теор. Число степеней свободы n для двух сопряженных выборок равно n – 2.

Если t_факт ³ t_теор, то значение коэффициента корреляции статистически существенно, а когда t_факт < t_теор коэффициент корреляции недостоверен. В рассматриваемом примере t_факт = 6,43, а t_теор = 2,26. Так как t_факт > t_теор вычисленное значение коэффициента корреляции является статистически достоверным.

Иногда возникает необходимость дать оценку доли влияния факторного признака (содержание гумуса) на результативный (бонитет). Ориентировочно это можно сделать по коэффициенту детерминации d. Численно он равен квадрату коэффициента корреляции:

d = r² = 0,9² = 0,81.

Величина коэффициента детерминации показывает, что балл оценки почвы примерно на 81% определен содержанием в ней гумуса.

Задание 4.а. Выполните корреляционный анализ данных, оцените достоверность коэффициента корреляции и сделайте выводы:

4.1. Х 8,7 8,5 7,9 9,6 9,4 8,2 8,2 8,0 7,9 7,6

У 20,9 20,4 20,1 21,7 21,4 20,3 20,5 20,1 19,7 19,4

4.2. Х 21,9 20,7 20,1 20,0 19,5 20,8 22,1 21,6 18,9 21,0 23,1 22,6

У 16,9 17,0 16,1 16,7 16,1 16,6 16,2 17,2 15,3 17,2 15,1 14,9

4.3. Х 38,3 38,5 37,9 29,6 29,4 38,0 38,2 38,0 37,9 37,8 34,6

У 0,93 0,84 0,91 1,17 1,14 0,83 0,95 0,81 1,07 1,14 1,08

4.4. Х 20,1 21,7 19,9 21,0 22,1 22,6 21,9 20,7 20,1 21,6 19,5

У 15,8 16,7 16,3 16,6 16,2 17,2 16,9 17,9 16,1 15,3 17,2

4.5. Х 98,0 98,5 97,9 89,6 89,8 98,2 98,0 88,9 97,3 97,0 95,7 93,1

У 60,9 60,4 60,1 61,7 61,4 60,3 60,5 60,1 59,7 59,4 61,3 58,7

4.6. Х 15,3 17,0 15,6 16,9 16,1 16,6 16,8 17,0 16,1 16,7 17,4 14,9

У 20,1 20,0 21,9 20,7 20,8 22,1 19,5 21,0 23,1 21,6 18,9 22,6

4.7. Х 38,3 38,5 37,9 29,6 29,4 38,0 38,2 38,0 37,9 37,8 34,6

У 7,95 8,81 9,07 9,14 8,08 8,93 8,84 7,91 9,17 9,14 8,83

4.8. Х 17,2 16,9 17,9 15,8 16,7 16,3 16,6 16,216,1 15,3 17,2 16,0

У 20,1 21,7 19,9 21,0 22,1 22,6 21,9 20,7 20,1 21,6 19,5 20,4

4.9. Х 68,7 68,5 67,6 66,6 66,8 68,2 68,0 68,6 67,3 67,0 65,7 63,1

У 50,9 50,4 50,1 51,7 51,4 50,3 50,5 50,1 59,7 59,4 51,3 58,7

4.10. Х 55,3 57,0 55,6 56,9 56,5 56,6 56,8 57,0 56,5 56,7 57,4 54,9

У 70,7 70,0 77,9 70,7 70,8 77,7 79,5 77,0 73,7 77,6 78,9 77,6

4.11. Х 58,5 58,5 57,9 59,6 59,4 58,0 58,5 58,0 57,9 57,8 54,6

У 8,25 8,61 9,17 9,14 8,08 8,93 8,84 8,91 9,07 9,14 8,83

4.12. Х 97,2 96,9 97,9 95,8 96,7 96,3 96,6 96,296,9 95,3 97,2 96,0

У 40,4 44,7 39,9 44,0 44,4 44,6 44,9 40,7 40,4 44,6 39,5 40,4

При изучении зависимостей нередко возникает потребность дать количественную оценку связи, то есть узнать, как изменится результативный показатель (У) при изменении факторного (Х) на единицу его измерения. Например, на сколько баллов изменится бонитет почвы при изменении содержания гумуса на 1%?

Чтобы получать ответы на подобные вопросы применяют регрессионный анализ. Для его выполнения используют те же данные, что и для корреляционного анализа. Однако, в отличие от корреляционного (парная корреляция), регрессионный анализ не ограничен требованием линейности связи и может применяться при любой ее форме.

Для выполнения регрессионного анализа данных также может быть использован MS Excel. В первую очередь нужно установить вид зависимости между данными, а затем выбрать математическую функцию, наиболее точно ее описывающую. Excel позволяет легко решить обе эти задачи.

Для этого по данным, использованным для корреляционного анализа, построим точечную диаграмму («Мастер диаграмм» – «Точечная»). В плоскости координат мы получим корреляционное поле точек (рис. 3).

Рис. 3. Корреляционное поле точек и линия тренда при зависимости, близкой к прямолинейной

Кликнув правой клавишей мыши по одной из точек, в появившемся контекстном меню включим «Добавить линию тренда». Так как по умолчанию компьютер добавляет линейный тренд, то каким бы ни было корреляционное поле точек, мы всегда получим прямую линию (рис. 4). Для того, чтобы получить линию тренда, соответствующую фактическому характеру зависимости, необходимо кликнуть правой клавишей мыши на линию тренда и выбрать команду «Формат линии тренда». В открывшемся окне перейти в раздел «Тип» и выбрать «Полиноминальная». В результате мы получим линию тренда, соответствующую фактическому характеру связи.

Уравнение регрессии (регрессионная модель) может быть получено прямо на диаграмме. Для этого в контекстном меню, вызываемом кликом правой клавиши мыши по линии тренда, выбираем «Формат линии тренда», переходим во вкладку «Параметры» и ставим отметку у пункта «Показывать уравнение на диаграмме».

На рисунке 4 показаны примеры уравнений регрессии для полиноминального (правильно) и линейного (неправильно) трендов.

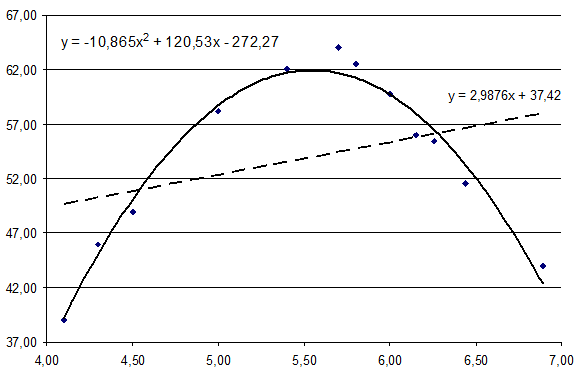
Рис. 4. Корреляционное поле точек и линия тренда при нелинейной зависимости:

_______ – полиноминальный тренд (правильно);

- - - - - - – линейный тренд (неправильно).

Уравнение линейной регрессии может быть получено в MS Excel также при помощи функции «Регрессия» в «Пакете анализа». В окне регрессионного анализа сначала указывают входной интервал данных результативного показателя, затем – факторного. Важно помнить, что в регрессионном анализе имеет принципиальное значение, какой признак является результативным, а какой – факторным.

Выполнив необходимые действия, на новом рабочем листе получим результаты регрессионного анализа:

Регрессионная статистика
Множественный R	0.917966025
R-квадрат	0.842661623
Нормированный R-квадрат	0.825179581
Стандартная ошибка	2.411135329
Наблюдения
Дисперсионный анализ
	df	SS	MS
Регрессия		280.2232924	280.2232924
Остаток		52.32216216	5.813573574
Итого		332.5454545
	Коэффициенты	Стандартная ошибка	t-статистика
Y-пересечение	14.14162162	5.306570776	2.664926601
Переменная X 1	6.454054054	0.929612745	6.942734046

Нужные нам данные содержатся в двух нижних строках в столбце «Коэффициенты». «Y-пересечение» – это коэффициент а. Коэффициент регрессии b имеет название «Переменная Х 1».

Подставим найденные значения коэффициентов в уравнение (для прямой - Y = a + bx):

Y = 14,14 + 6,45 x.

Полученное уравнение регрессии может быть использовано для расчета бонитета почв по новым данным содержания гумуса. Следует помнить, что вычисляемые таким образом результаты имеют приближенный (прогнозный) характер. При вычислениях в пределах изученной области определения переменной х (интерполяция) результаты более надежны, чем при вычислениях за пределами этой области (экстраполяция).

Вычислим, например, возможную величину бонитета почвы при снижении содержания гумуса до 3%:

Y = 14,14 + 6,45 × 3 = 33,5.

Расчет по регрессионной модели позволил установить, что при снижении содержания гумуса в почве до 3% ее бонитет также снизится и составит около 33,5 баллов.

Задание 4.b. Выполните регрессионный анализ данных из задания 4.1. и запишите уравнения регрессии.

Примените приемы интерполяции и экстраполяции для вычисления значений результативной и факторной переменных.

Калькулятор

Множественный линейный регрессионный анализ в MS Excel

Для выполнения анализа используется функция ЛИНЕЙН. Доступ к ней осуществляется через меню «Вставка» (в Excel 2000-2003) или с помощью кнопки «Вставка функции»:

Предварительно ставим курсор в свободную ячейку и вставляем функцию ЛИНЕЙН. В диалоговом окне функции указываем диапазон ячеек, содержащих значения результативного показателя (У). Значения факторных признаков (Х₁, Х₂…Х_n) указываем единым массивом. В строках «Конст» и «Статистика» указываем логическое значение «Истина» (можно ввести цифру «1»).

В выбранной в начале ячейке получаем одно число. Ставим на него курсор мыши, нажимаем левую клавишу и выделяем диапазон ячеек шириной, соответственно количеству столбцов с данными (Х₁, Х₂…Х_n и У), а высотой – 5 строк. Затем нажимаем F2 и Ctrl+Shift+Enter (одновременно). После этого в выделенном диапазоне ячеек получаем результаты. Верхняя строка таблицы содержит коэффициенты уравнения регрессии, остальные – регрессионную статистику. Коэффициенты регрессионного уравнения выстроены в следующем порядке: m _n, m _n-1… т ₁, b. Здесь m _n… т ₁ – коэффициенты регрессии при соответствующих переменных, b – свободный коэффициент уравнения. Все коэффициенты могут принимать любые числовые значения.

Уравнение множественной линейной регрессии имеет вид:

У = т ₁ х ₁ + т ₂ х ₂ + … т _n х _n + b.

Задание 4.с. Выполните множественный регрессионный анализ зависимости диаметра гнили стволов деревьев (по стадиям) от набора факторов (возраст дерева, диаметр ствола, класс роста и развития, количество мертвых сучьев, протяженность зоны мертвых сучьев, количество плодовых тел, высота прикрепления плодового тела). Загрузить данные "диаметр гнили стволов" и выполнить расчет.

Дата добавления: 2015-08-31