Основные термины и обозначения

А – явление (результат действия факторов, например, урожайность);

В – фактор (переменная величина, действующая на явление);

а_i – отдельный ранг (класс) явления;

b_j – отдельный ранг (класс) фактора;

Р_ai – условная вероятность состояния явления в зависимости от ранга фактора;

Р_bj – условная вероятность состояния фактора в зависимости от ранга явления;

Н(А) – неопределенность по состоянию явления, бит;

Н(В) – неопределенность по состоянию фактора, бит;

i – порядковый номер ранга явления;

j – порядковый номер ранга фактора;

I – информация, бит. Может быть отрицательной, что указывает на дезинформацию;

Т – общее количество информации, передающейся от фактора (В) к явлению (А), бит;

К – коэффициент эффективности передачи информации от фактора к явлению. Вычисляется по формуле:

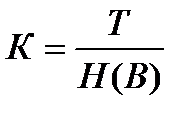
Коэффициент К – величина безразмерная, при этом фактор В рассматривается как передатчик информации, а явление А – как приемник. Величина Т (А,В) никогда не может быть больше минимального значения одной из сопоставляемых неопределенностей. Поэтому величина коэффициента К максимальна, когда от параметра передается к явлению количество информации, равное минимальной неопределенности. При определении коэффициентов эффективности передачи информации от нескольких факторов (например, мощности гумусового горизонта, гранулометрического состава, элемента мезорельефа и т.п.) наибольшее значение в формировании урожайности будет иметь тот, для которого больше коэффициент К. При помощи этого коэффициента можно установить степень влияния каждого фактора на урожайность (явление А) и распределить их в строгой последовательности один относительно другого.

С – коэффициент связи для нахождения специфичных состояний, то есть состояний фактора (В) в которых явление (А) устойчиво. Рассчитывается по формуле:

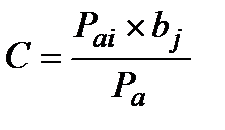
где Р_a – условная вероятность по рангу явления.

С помощью информационно-логического анализа можно получить модели таких сложных явлений как урожайность сельскохозяйственных культур или почвенное плодородие.

Для создания математической модели урожайности требуется получить исходные данные о фактической урожайности сельскохозяйственной культуры при установленных лабораторными анализами и наблюдениями величинах основных факторов ее определяющих (табл. 3).

Данные, для выполнения информационно-логического анализа на занятии выдаются в электронном виде в таблице MS Excel.

Сначала исходные данные должны быть проранжированы, то есть распределены по классам соответственно величинам урожайности и каждого фактора. При этом может встретиться два варианта: 1) факторы, влияющие на параметр (урожайность), - качественные, например, типы почв; 2) факторы, влияющие на параметр, - количественные, например, содержание гумуса, элементов питания, тепло- и влагообеспеченность и т.д.

В первом варианте таблица для ранжирования данных будет одна, во втором количество таблиц будет равно числу факторов.

Сначала вычисляют количество рангов К по формуле:

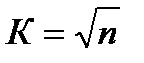
где n – количество данных.

В рассматриваемом примере при n = 25 количество рангов составит:

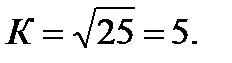
Затем вычисляют ширину рангов i:

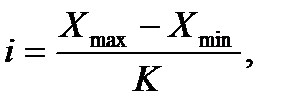
где Х_max – максимальное значение в ранжируемом ряду данных;

Х_min – минимальное значение в ранжируемом ряду данных.

Калькулятор

Найдем размах ранга при ранжировании данных по урожайности:

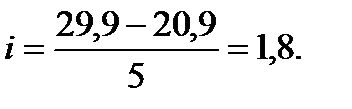
Таблица 3. Исходные данные для информационно-логического анализа

№ п/п	Урожайность пшеницы, ц/га	Почвенные факторы урожайности
М, см	Г, %	рН	NO3, мг/кг	Р2О5, мг/кг	К2О, мг/кг	Рв, %	Nв, %
1.	23,5		5,7	6,2	12,1	11,7	10,8	0,22	0,51
2.	27,9		5,7	6,8		23,1	12,1	0,23	0,32
3.	28,2		5,3	7,2	4,8	8,4	18,9	0,19	0,41
4.	28,3		5,9	6,6	8,1	12,7	23,6	0,13	0,38
5.	22,7		6,1	6,8	3,7	3,7	29,6	0,17	0,23
6.	23,9		2,9	7,4	4,1	3,5	8,1	0,13	0,19
7.	22,9		6,4	6,4	14,3	4,9	13,6	0,15	0,31
8.	24,3		5,7	6,3	9,5	6,8	14,5	0,19	0,24
9.	22,7		9,1	7,1	6,9	4,5	13,6	0,14	0,27
10.	26,0		8,1	6,9	21,7	13,8	22,4	0,19	0,33
11.	20,9		3,8	7,2	4,7	7,6	8,7	0,14	0,51
12.	26,2		6,5	6,7	13,4	16,1	12,8	0,16	0,27
13.	29,2		4,8	7,7	5,9	4,2	9,3	0,16	0,17
14.	29,5		7,3	6,8	17,3	21,6	19,6	0,23	0,47
15.	29,7		5,8	7,3	12,7	8,4	27,4	0,22	0,19
16.	29,8		7,4	6,9	18,9	15,8	16,7	0,2	0,34
17.	22,5		6,8	7,2	4,7	7,3	11,7	0,13	0,25
18.	25,2		6,3	6,7	3,9	17,4	16,3	0,16	0,47
19.	23,7		8,2	6,3	19,1	17,3	21,4	0,17	0,45
20.	25,7		5,9	6,3	2,3	8,1	12,1	0,2	0,56
21.	26,9		9,2	6,4	8,4	9,5	13,2	0,17	0,29
22.	26,2		7,2	6,2	16,8	25,3	17,1	0,2	0,36
23.	24,5		4,3	7,6	11,7	16,1	31,6	0,21	0,18
24.	29,9		9,7	6,4	25,1	19,6	27,9	0,24	0,57
25.	21,8		3,4	6,2	4,9	25,3	30,5	0,18	0,27

М – мощность гумусового горизонта почвы, Г – содержание гумуса, рН – кислотность (щелочность) водной суспензии почвы; NO₃ – содержание нитратного азота, Р₂О₅ – содержание доступного растениям фосфора, К₂О – содержание обменного калия, Рв – валовое содержание фосфора, Nв – валовое содержание азота

Так как данные по урожайности пшеницы выражены с точностью до десятых, то и ширину размаха ранга тоже целесообразно округлять до десятых, после чего она составит 1,8.

Вычислим ранги для урожайности. Первый ранг будет начинаться с минимального числа ряда. Суммировав Х_min и i получим конец первого ранга:

20,9 + 1,8 = 22,7.

Таким образом, первый ранг будет иметь вид: 20,9-22,7.

Суммируя конечное значение первого ранга со значением размаха, получим конец второго ранга:

22,7 + 1,8 = 24,5.

Таким же образом вычисляют концы остальных рангов.

Последний ранг должен заканчиваться максимальным числом ряда – Х_max. Следует иметь ввиду, что по причине округления величины i, вычисленный конец последнего ранга может быть немного меньше или больше Х_max. Этим отклонением следует пренебречь и установить концом последнего ранга Х_max.

Таким же образом ранжируют данные по каждому из факторов и заносят их в таблицы, подобные таблице 4.

Таблица 4. Разноска данных: Мощность гумусового горизонта

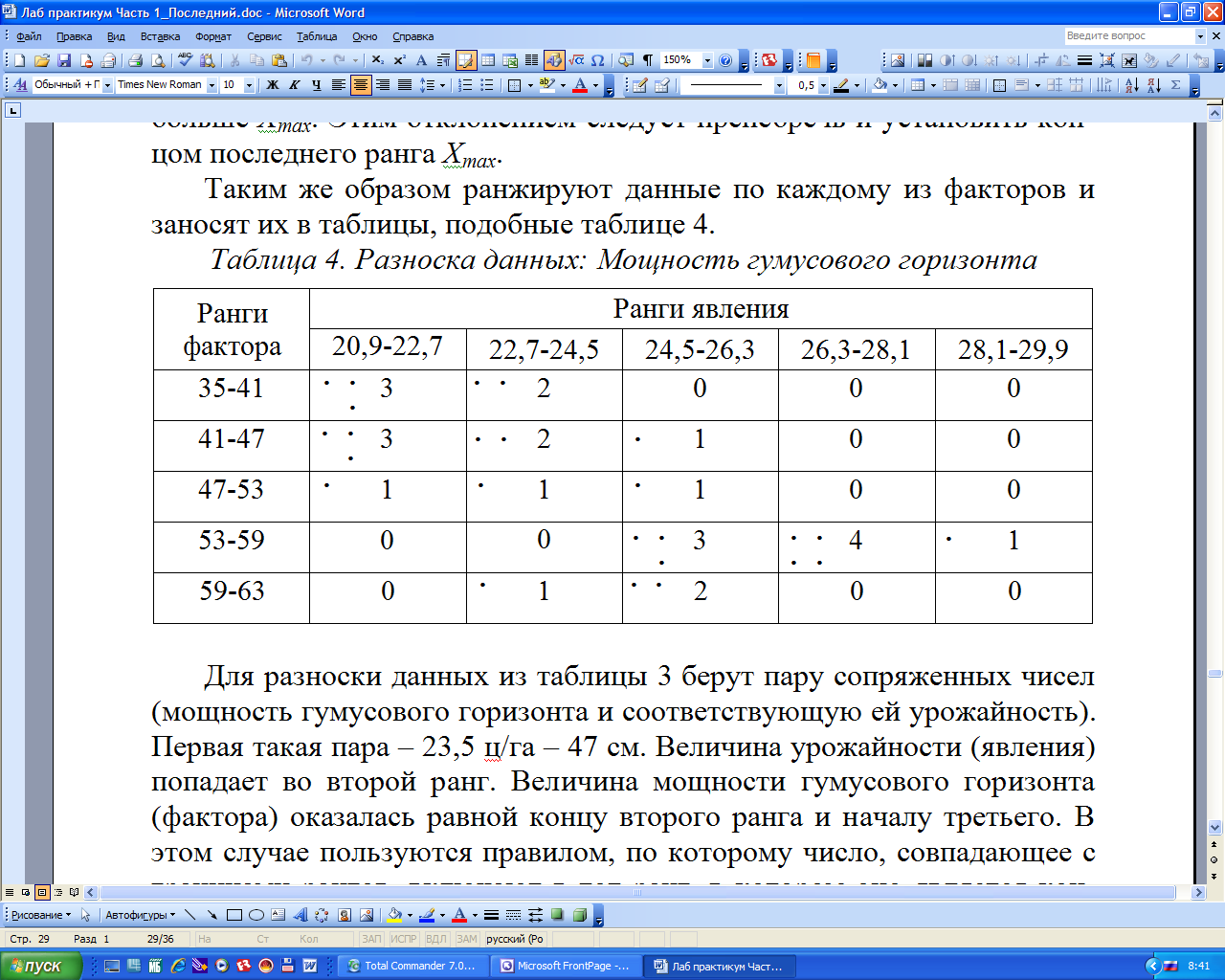
Для разноски данных из таблицы 3 берут пару сопряженных чисел (мощность гумусового горизонта и соответствующую ей урожайность). Первая такая пара – 23,5 ц/га – 47 см. Величина урожайности (явления) попадает во второй ранг. Величина мощности гумусового горизонта (фактора) оказалась равной концу второго ранга и началу третьего. В этом случае пользуются правилом, по которому число, совпадающее с границами рангов, включают в тот ранг, в котором оно является концом. Поэтому число 47 следует включить во второй ранг фактора. Таким образом, первая пара данных дает точку связи на пересечении второй строки и второго столбца. Для того, чтобы зафиксировать в таблице этот факт в данной ячейке ставят точку. Подобным образом выполняют разноску всех данных по первому фактору. Для подсчета попадающих в ячейки точек связи пользуются следующими обозначениями:

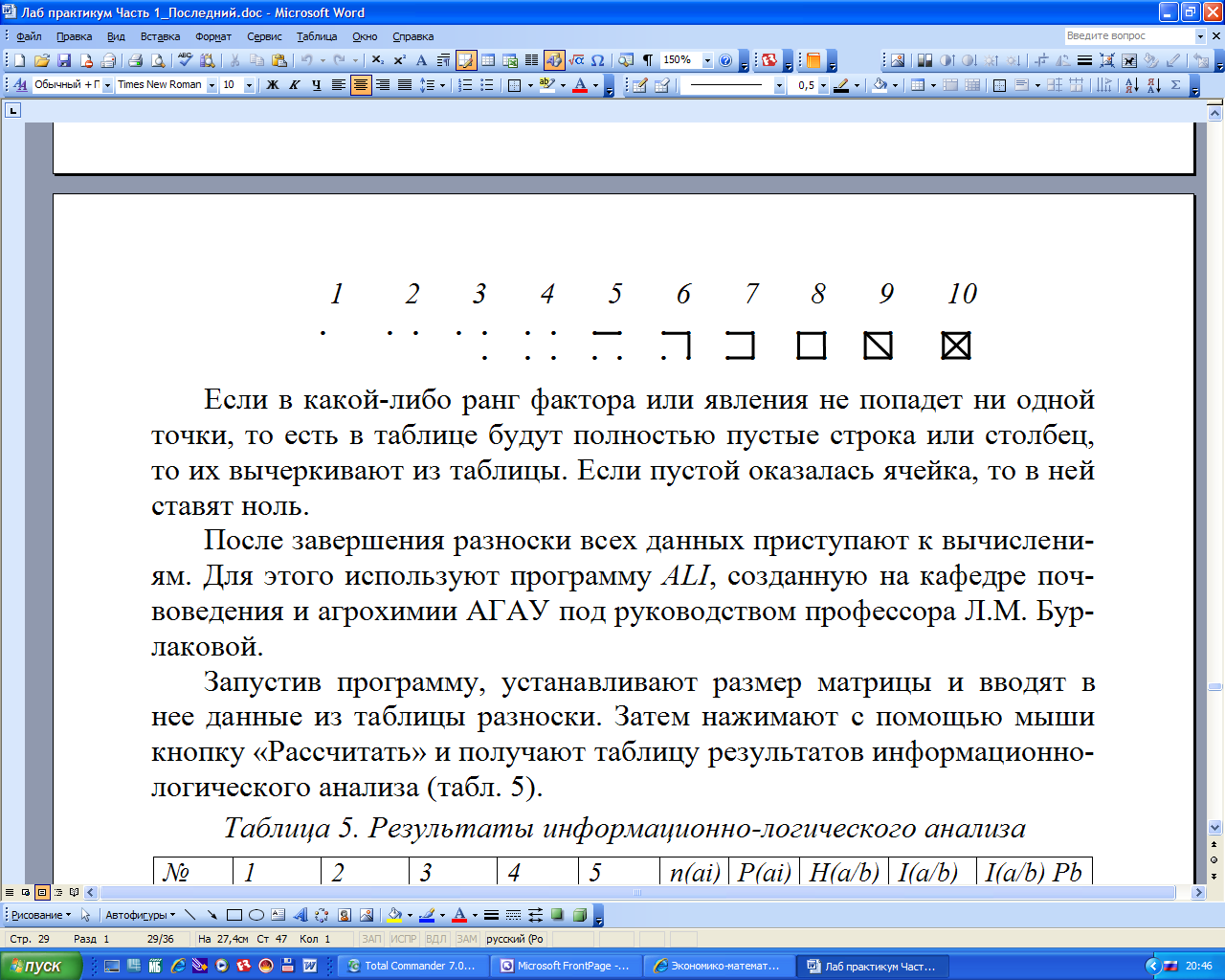
Если в какой-либо ранг фактора или явления не попадет ни одной точки, то есть в таблице будут полностью пустые строка или столбец, то их вычеркивают из таблицы. Если пустой оказалась ячейка, то в ней ставят ноль.

После завершения разноски всех данных приступают к вычислениям. Для этого используют программу ALI, созданную на кафедре почвоведения и агрохимии АГАУ под руководством профессора Л.М. Бурлаковой.

Запустив программу, устанавливают размер матрицы и вводят в нее данные из таблицы разноски. Затем нажимают с помощью мыши кнопку «Рассчитать» и получают таблицу результатов информационно-логического анализа (табл. 5).

Таблица 5. Результаты информационно-логического анализа

№	1	2	3	4	5	n(ai)	P(ai)	H(a/b)	I(a/b)	I(a/b) Pb
1	0.6	0.4					0.2	0.9700	1.1612	0.2321
С	2.1429	1.6667
2	0.5	0.3332	0.1667				0.24	1.4592	0.672	0.1613
С	1.7856	1.3882	0.5954
3	0.3332	0.3332	0.3332				0.12	1.5848	0.5464	0.0656
С	1.19	1.3882	1.19
4			0.375	0.5	0.125		0.32	1.4055	0.7257	0.2321
С			1.3393	3.125	3.125
5		0.3332	0.6667				0.12	0.9181	1.2131	0.1456
С		1.3882	2.3811
n(bj)
P(bj)	0.28	0.24	0.28	0.16	0.04

H(A) = 2.1312

H(B) = 2.2187

Т = 0.8367

К = 0.3770

В первую очередь анализируют коэффициенты столбца информации I(a/b). Их значения не должны быть отрицательными. Отрицательные значения информации указывают либо на наличие обратной связи, либо на дезинформацию. Наличие обратной связи в математической модели недопустимо, так как приводит к искажению результата. Поэтому принимают меры к исключению обратной связи. От дезинформации можно попытаться избавиться, увеличив количество наблюдений.

Информационно-логический анализ позволяет установить значения фактора, в которых явление наиболее устойчиво, то есть принимает состояние, вероятность наступления которого наибольшая. Для этого используют коэффициенты связи С. Чем больше величина коэффициента связи между фактором и явлением, тем, следовательно, устойчивее явление. Наибольшее значение С при анализе таблицы 5 обнаруживаем в четвертом ранге фактора и четвертом и пятом рангах явления. Следовательно, наиболее вероятный размер урожайности – 26,3-29,9 ц/га при мощности гумусового горизонта 47-53 см.

Для того, чтобы наглядно выразить характер связи и ее количественные значения, строят график зависимости явления от фактора по коэффициентам связи С (см. табл. 5 и рис. 5).

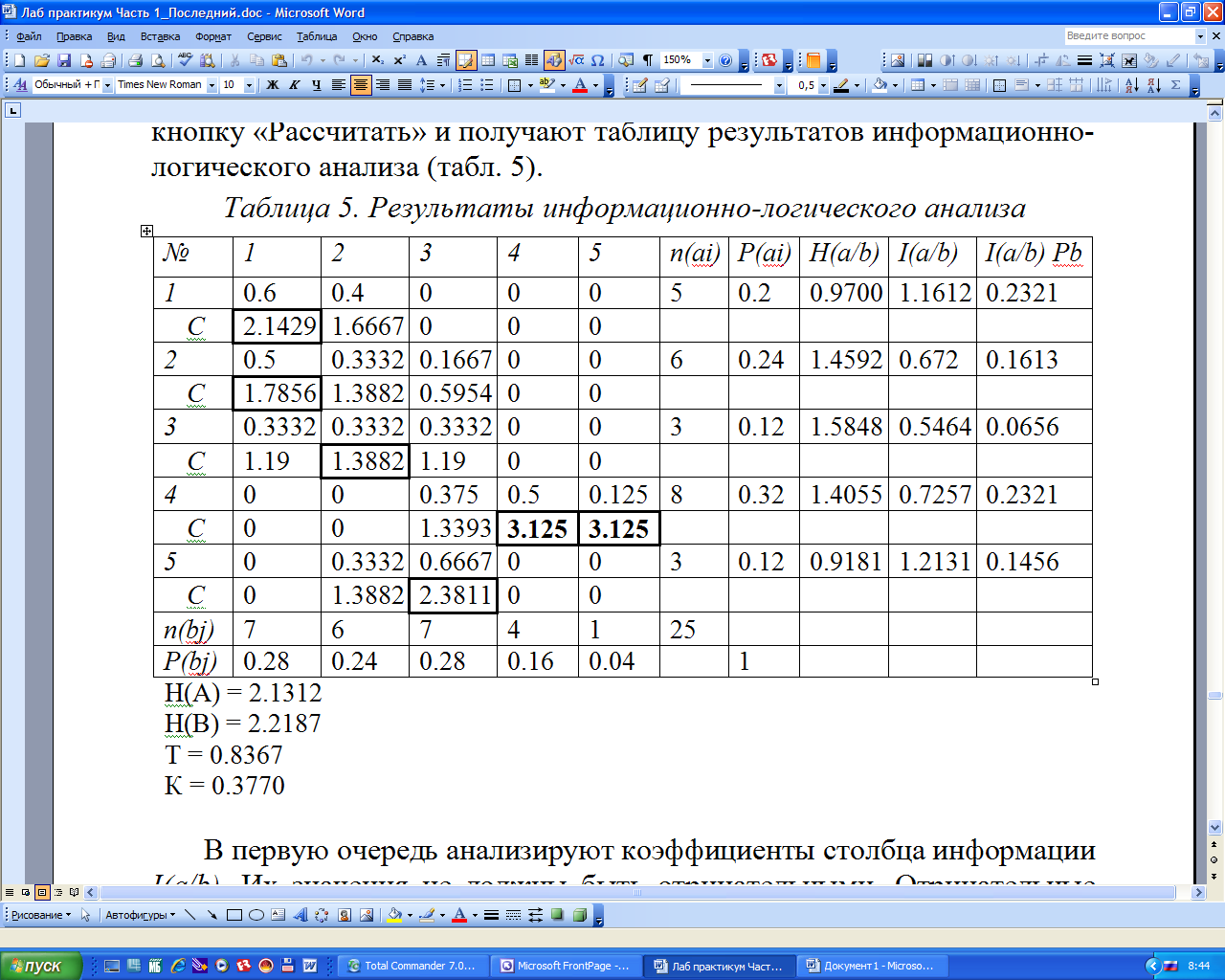
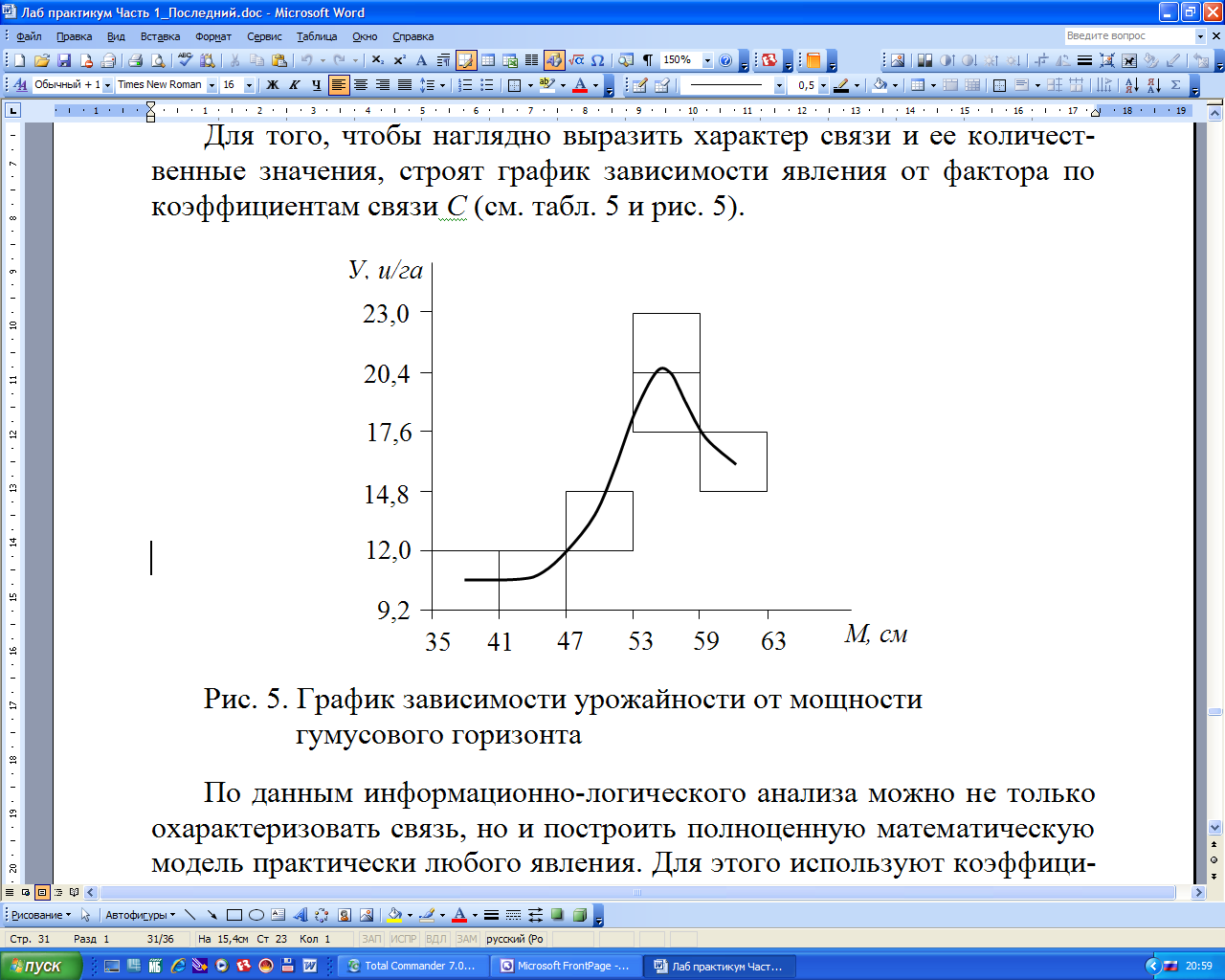
Рис. 5. График зависимости урожайности от мощности гумусового горизонта

По данным информационно-логического анализа можно не только охарактеризовать связь, но и построить полноценную математическую модель практически любого явления. Для этого используют коэффициенты эффективности передачи информации К от фактора к явлению. Чем больше величина К, тем сильнее влияние фактора на явление, поэтому в модели этот фактор располагают первым. Далее располагают факторы по мере уменьшения величин вычисленных для них коэффициентов К. Одинаковые или очень близкие по значению коэффициенты (различаются в сотых, или тысячных) объединяют и в модели берут в скобки. Факторы в модели должны быть связаны одной из трех логических функций: нелинейного произведения, конъюнкции или дизъюнкции. Так как урожайность сельскохозяйственной культуры – это среднее значение суммарного действия всех факторов, то при ее моделировании следует использовать нелинейное произведение. В итоге получаем модель:

У_{яр.пшен.} = М рН_в (Г К₂О (N_в NО₃ (Р_в Р₂О₅))).

Данная модель может быть применена для прогнозирования урожайности культуры по величинам факторов; для определения величин управляемых факторов при заданном размере урожайности; для бонитировки и оценки почвы через урожайность.

Для расчетов по информационно-логической модели используют данные полевых и лабораторных исследований. С помощью таблиц разноски данных фактические значения факторов переводят в ранги и подставляют их в модель, записывая ее следующим образом:

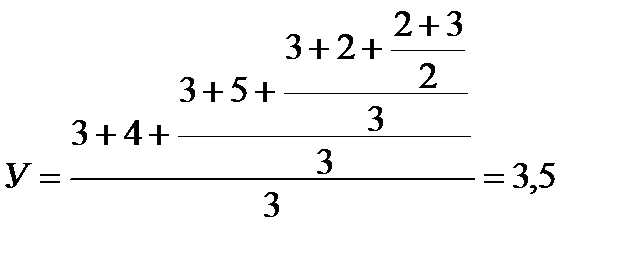
Вычисления начинают сверху, и выполняют действия, перемещаясь влево и вниз. Полученное значение ранга явления округляют до целого, за исключением половинных значений, как в приведенном выше примере. При округлении данного числа в соответствии с правилами, цифра 5 должна быть отброшена, и мы получим третий ранг урожайности. Однако, полученное расчетами значение ранга 3,5 означает, что величина прогнозируемой урожайности выше значений третьего ранга. Таким, образом, округление приводит к явному и довольно существенному занижению результата. Поэтому половинные значения урожайности не округляют, а используют для них половину соответствующего ранга. Так, значение 3,5 означает, что урожайность соответствует четвертому рангу, но не полностью, а только первой его половине: 26,3-27,2 (ц/га).

Рекомендуемая литература

1. Доспехов Б.А. Методика полевого опыта (с основами статистической обработки результатов исследований).- М.: Агропромиздат, 1985. -351 с.

2. Моисейченко В.Ф., Трифонова М.Ф., Заверюха А.Х., Ещенко В.Е. Основы научных исследований в агрономии. –М.: Колос, 1996. –336 с.

3. Овцинов В.И. Экономико-математические методы и моделирование в землеустройстве: Учебное пособие для студентов заочного обучения. –Барнаул: Изд-во АГАУ, 2004. -75 с.

4. Овцинов В.И. Экономико-математические методы и моделирование в почвенно-агрохимических исследованиях, землеустройстве, земельном и городском кадастре. Часть I. Математические методы оценки качества и подготовки информации к моделированию: методические указания к лабораторным занятиям /В.И. Овцинов, А.Б. Совриков. – Барнаул: РИО АГАУ, 2012. – 38 с.

5. Овцинов В.И., Совриков А.Б. Экономико-математические методы и моделирование в землеустройстве, земельном и городском кадастре: Электронный учебно-методический комплекс. –Барнаул, АГАУ, 2009.

6. Овцинов В.И. Основы научных исследований в овощеводстве и плодоводстве: Электронный учебно-методический комплекс. –Барнаул, АГАУ, 2007.

7. Рассыпнов В.А. Сборник задач и упражнений по методике опытного дела. –Барнаул: Алтайский СХИ, 1987. -63 с.

Дата добавления: 2015-08-31