Лучевое представление распространения электромагнитных волн в диэлектрических волноводах

Наиболее полное представление о характере электромагнитных процессов в диэлектрических волноводах (рис.1.1) можно получить на основе решения уравнений Максвелла (или вытекающих из них волновых уравнений) с соответствующими граничными условиями на границах сред и условием убывания поля на бесконечности [3,4].

Другой путь исследования – использование метода геометрической оптики (а так же различных модификаций). В соответствии с названием геометрическая (лучевая) оптика использует понятие лучей для описания распространения электромагнитных волн. При этом луч в каждой точке пространства совпадает с вектором, определяющим направление распространения волны, который, в свою очередь, перпендикулярен поверхности постоянных фаз электромагнитной волны. В геометрической оптике распространение волн рассматривают как распространение лучей без учета волнового характера поля. Можно строго доказать, что это представление будет тем точнее, чем меньше длина волн. В то же время на практике метод геометрической оптики в большинстве случаев более удобен, чем волновой подход, поскольку он позволяет упростить задачу и дать, таким образом, ясную, хотя и не такую полную, как при решении уравнений Максвелла, физическую картину явлений.

Распространение света в планарном диэлектрическом волноводе рассмотрим на примере распространения одного из световых лучей, который в результате полного внутреннего отражения света от границ раздела пленка – подложка и пленка – покрытие движется по зигзагообразному пути (рис. 1.4,б).

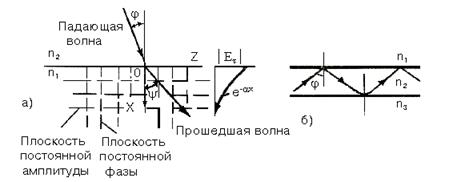
Рис1.4. Падение плоской волны на границу раздела двух сред.

Поскольку явления отражения и преломления на границах раздела диэлектриков играют важную роль в волноводных процессах, напомним кратко основные положения.

Если на границу раздела двух сред без потерь (рис.1.4,а) падает под углом 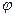плоская однородная электромагнитная волна, то в системе координат, представленной на рис.1.4, выражение для касательной компоненты электрического поля прошедшей волны можно представить следующим образом:

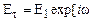
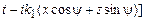(x>0),

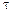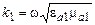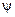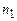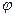где индексом отмеченысоставляющие, касательные к поверхности раздела; – постоянная распространения волны, падающей под углом в среде с показателем преломления Углы и 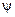связаны законом преломления Снеллиуса:

,

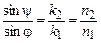где 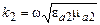, , 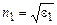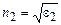– показатели преломления первой и второй сред соответственно.

Учитывая, что 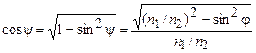(знак плюс перед корнем взят из физических соображений) и подставляя 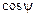в выражение для 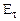, получаем

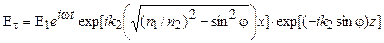. (1.1)

Плоская волна произвольной поляризации полностью отражается от границы раздела двух средств, если угол падения 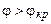, где 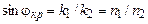. Проанализируем выражение (1.1).

1. Пусть 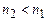, тогда величина 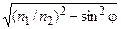– действительная для всех углов падения 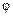. Преломленная волна, как следует из (1.1), в этом случае является плоской с постоянной амплитудой.

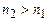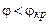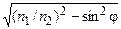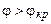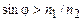2. Пусть , тогда для углов падения величина – действительная величина и преломленная волна попрежнему плоская однородная. Если же , то и 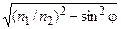– мнимая величина. В этом случае, взяв перед корнем знак минус (что необходимо из физических условий убывания волны при 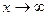), получим из (1.1)

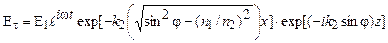. (1.2)

При этом плоскости постоянной амплитуды определяются уравнением 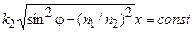и уже не совпадают с плоскостями постоянной фазы: .

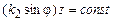Следовательно, при углах падения, когда 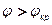, прошедшая волна не является однородной. Амплитуда преломленной волны экспоненциально затухает по мере удаления от границы раздела 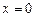, причем, коэффициент затухания .

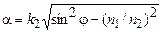Поскольку плоскости постоянной фазы перпендикулярны границе раздела, то волна, описываемая выражением (1.2), распространяется вдоль поверхности раздела (вдоль оси OZ – рис.1.4,а) с постоянной 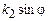, а амплитуда ее экспоненциально убывает по нормали к поверхности раздела. Такая волна, “прижатая” к поверхности раздела называется поверхностной. Она может существовать только при 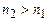(среда, из которой падает плоская волна оптически более плотная) и угле падения .

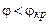Теперь рассмотрим планарный диэлектрический волновод (рис.1.4,б). Предположим, что внутри пленки луч идет к верхней границе. Если угол 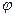между нормалью к поверхности пленки и направлением распространения луча больше критического угла падения, определенного выше ( 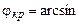n₁/n₂), то при 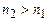(волна будет полностью отражаться от верхней границе пленки. После этого отраженный луч падает на нижнюю границу пленки и испытывает полное внутреннее отражение, поскольку 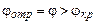(в этом случае 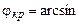n₃/n₂) Следовательно, волна, распространяясь в пленке зигзагообразно, осуществляет перенос энергии вдоль нее. Результирующее поле в пленке представляет собой сумму первоначальной и отраженной волн, поле в подложке и покрытии описывается выражением, аналогичным (1.2). Различные волноводные моды (см.гл. 2) представляют собой зигзагообразные волны.

Таким образом, выше на основе лучевого подхода, показана возможность существования в планарном диэлектрическом волноводе направляемой поверхностной электромагнитной волны, основная энергия которой сосредоточена внутри волновода.

Далее перейдем к количественному исследованию характеристик поверхностных волн, используя строгий подход на основе решений уравнений Максвелла с соответствующими граничными условиями. При этом основное внимание уделим “свободным” направляемым поверхностным волнам, т.е. волнам, не связанным с конкретными источниками их возбуждения. Возбуждение поверхностных волн является более сложной задачей и требует отдельного рассмотрения.

2. ВОЛНЫ В ПЛАНАРНОМ ДИЭЛЕКТРИЧЕСКОМ ВОЛНОВОДЕ

Дата добавления: 2015-08-31