Упражнения и задачи

End

End

Function aksi(d)

End

Enddo

Do while(abs(aksi2-aksi1).gt. eps)

Endif

Else

If(ak.eq. 1) then

!для K=1

d2 = 1 - 2*sqrt(2)/pi

!для K>1

d2 = 1 - b - 2/pi

!нижняя граница области решения

aksi1 = aksi(d1)

!верхняя граница области решения

aksi2 = aksi(d2)

!итерационная процедура;

!цикл пока не достигнута заданная точность

!обращения к функции вычисления параметра кривизны

d1 = delta(aksi1)

d2 = delta(aksi2)

!обращения к функции решения квадратного уравнения

aksi1 = aksi(d1)

aksi2 = aksi(d2)

!определение h

h = (aksi1+aksi2)/2 * 2*pi/alambda * sqrt(e2-e3)

!вывод результата

print *, h

!--------------------------------------------------------------

!Функция вычисления корня уравнения по формуле (3.21а)

!переменные, получаемые из beta2

common /cblock/ a,ak,m,b

!дискриминант квадратного уравнения

dis = (1-b-d)**2 + 4*(a+d)*(a-b-m)

if(dis.lt. 0) stop 'Недопустимое сочетание вх. данных'

!корень уравнения

aksi = 1 - ((sqrt(dis)-1+b+d) / (2*(a+d)))**2

return

!--------------------------------------------------------------

!Функция вычиления параметра кривизны по формуле (3.21б)

function delta(x)

!переменные, получаемые из beta2

common /cblock/ a,ak,m,b

!ф-ция f1

f1 = atan(sqrt(1/x**2-1))

f1 = (f1 + atan(sqrt(ak/x**2-1))) / 3.14159

!числитель

t2 = b + (1-b)*sqrt(1-x) - f1

!знаменатель

t1 = sqrt(1-x) -1+x

!параметр кривизны

delta = t2/t1

return

!--------------------------------------------------------------

*⁾программмы к разделам 3.2.2 и 3.3.2 разработаны доцентом Д.В.Багно

1. Пояснить достоинства и недостатки ДВ, показанных на рис.1.1, с точки зрения требований, предъявляемых к базовой линии

передачи (см. раздел 1.1).

2. Предложить новые ДВ, удовлетворяющие требованиям раздела 1.1.

3. Показать, что вдали от критических частот коэффициент затухания 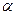близок к коэффициенту затухания для однородных плоских волн, распространяющихся в безграничной среде, параметры которой совпадают с параметрами диэлектрической пленки.

4.Вывести формулы для определения доли мощности, переносимой в пленке, подложке и покрытии для асимметричного планарного волновода. (Указание: использовать идеологию раздела 2.7).

5. Получить формулы (2.35) и (2.37).

6. Получить формулы, аналогичные (2.35), (2.37), для четных (нечетных) Н - и Е-мод.

7. Получить дисперсионные уравнения, аналогичные (2.26), (2.27), для Н - и Е-мод в планарном ДВ на металлической подложке (см. рис.1.1,ж; рис. 2.7). (Указание: поле в диэлектрической пленке на металлической подложке должно удовлетворять граничным условиям на поверхности металла; из волн типа Е в такой структуре могут существовать только четные, из волн типа Н – только нечетные.)

8. Вывести формулы для структуры поля Н - и Е-мод в Н-образном металлодиэлектрическом волноводе (см. рис.1.1,е; рис. 2.8.). (Указание: поле в ДВ должно удовлетворять граничным условиям на металлических пластинах, которые полагаются бесконечными. Основной волной является волна магнитного типа, вектор 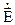которой имеет единственную y-составляющую, причем все составляющие не зависят от координаты y, перпендикулярной металлическим пластинам. Эта волна полностью аналогична основной волне магнитного типа H₀ планарного симметричного ДВ).

9. Получить ограничения (см. таблицу в разделе 3.3.) на параметры диэлектрического волновода при решении дисперсионного уравнения по методу аппроксимации.

10. Написать программу для расчета поперечных волновых чисел h для H- и Е-волн планарного однородного изотропного диэлектрического волновода, используя метод “половинного деления”.

11. Написать программу для расчета поперечных волновых чисел h для H- и Е-волн планарного однородного диэлектрического волновода, используя метод аппроксимации.

12. Дать лучевую трактовку распространения электромагнитных волн в планарном диэлектрическом волноводе.

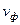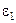13. Найти фазовую скорость двух низших волн магнитного типа, распространяющихся вдоль симметричного планарного ДВ толщиной 2d=2см с относительной проницаемостью =2,9, =1,0. Длина волны генератора 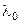=3,2см. Построить графики распределения поперечных составляющих () векторов поля в направлении, перпендикулярном диэлектрической пластинке (аналогично рис. 4.1).

Ответ: 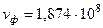, м/с, 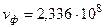, м/с.

Рис. 4.1. Распределения составляющих .

14. Определить значение 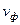волн электрического типа, которые могут распространяться в планарном ДВ на металлической подложке. Толщина пластины t=15 мм, =2,25, =1,0. Частота поля 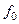=10 ГГц.

15. Определить значение 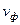волн магнитного, которые могут распространяться в симметричном планарном ДВ. Толщина пластины t=15 мм, =2,25, =1,0. Частота поля 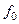=10 ГГц.

16. Определить значение 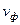волн электрического, которые могут распространяться в симметричном планарном ДВ. Толщина пластины t=15 мм, =2,25, =1,0. Частота поля 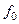=10 ГГц.

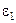17. Определить распространяющиеся типы волн вдоль симметричного планарного ДВ толщиной 2d=12мм при частоте поля 10 ГГц? Диэлектрические проницаемости =3, =1,0.

Ответ: Н₀, Н₁, Е₀, Е₁.

18. Определить толщину симметричного ДВ из полистирола ( =2,56), при которой вдоль ДВ распространяется только основная волна магнитного типаН₀. Длина волны генератора =4,5см, = =1,5.

19. Определить фазовую скорость волны типа Н₀, распространяющуюся в асимметричном ДВ толщиной t=10 мм, =2,9, =1,0, =2,7; длина волны генератора 16 мм. Построить график распределения компоненты () в направлении, перпендикулярном диэлектрической пластине.

Указание: см. задачу 13.

20. Определить фазовую скорость, длину волны и построить график распределения компоненты () в направлении, перпендикулярном диэлектрической пластине для основной волны магнитного типа, распространяющейся вдоль планарного полистиролового ДВ ( =2,56) толщиной t=16 мм на металлической подложке. Длина волны генератора 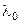=32 мм, 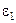=1,0.

21. Определить размер t оптического ДВ, при котором в нем распространяется только волна основного магнитного типа Н₀ (см. рис. 2.1,а, б). Параметры ДВ: n ₁ =1,0, n₂=1,613, n₃=1,516; длина волны лазера =0,63 мкм.

22. Найти фазовую скорость 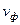двух низших волн электрического типа, распространяющихся вдоль симметричного планарного ДВ толщиной 2d=2см с относительной проницаемостью =2,9, 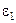=1,0. Длина волны генератора 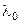=3,2см. Построить графики распределения поперечных составляющих (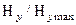) векторов поля в направлении, перпендикулярном диэлектрической пластинке (аналогично рис. 4.2).

23. Определить значение 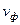волн магнитного типа, которые могут распространяться в планарном ДВ на металлической подложке. Толщина пластины t=15 мм, =2,25, =1,0. Частота поля 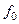=10 ГГц.

24. Определить фазовую скорость, длину волны в планарных оптических ДВ с основной магнитной волной Н₀ толщиной 2d=2мкм,n ₂ =1,7, n₁= n₃=1,65. Длина волны лазера =0,63 мкм.

25. Вывести формулы для определения коэффициента затухания 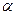волны типа при толщине ДВ 2d=10 мм, длине волны генератора =24 мм и параметрах диэлектрика =2,7,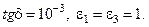

Ответ:

Указание: воспользоваться результатами раздела 2.7.

26. Вывести формулу для расчета мощности, переносимой основной волной магнитного типа в Н-образной линии передачи (см. рис.1.1,е; рис. 2.8). Рассчитать величину переносимой мощности в линии с размерами 2d=25 мм, b=15 мм. Диэлектрик – полистирол с =2,56, =1,0; длина волны генератора 4 см; значение амплитуды напряженности электрической -компоненты А_н=30 В/см.

Ответ: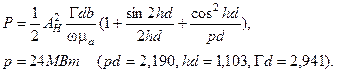

27. Определить длины волн Н₀, Н₁, распространяющихся вдоль планарного ДВ толщиной 2d=10 мм с =2.8, =1,0 при частоте поля f₀=12 ГГц.

Ответ: =16,78 мм для волны типа Н₀; =24,74 мм для волны типа Н_1.

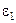28. Установить, в пределах какого диапазона частот вдоль планарного диэлектрического волновода на металлической подложке может распространяться только основная волна магнитного типа. Толщина t=12 мм, =2,9, =1,0.

Ответ: 4,53ГГц < f< 13,6ГГц.

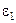29. Установить, в пределах какого диапазона частот вдоль планарного симметричного диэлектрического волновода жке может распространяться только основная волна магнитного типа. Толщина t=10 мм, =2,9, =1,0.

30. Вывести формулу для определения доли мощности, переносимой волной типа Н₀ внутри планарного симметрического ДВ. Провести численный расчет следующих данных 2d=8 мм, = 3,8, =1,0; длина волны генератора =30 мм.

Ответ: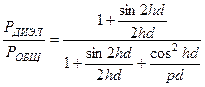

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

Основнаой

1. Унгер Х.Г. Планарные и волоконные оптические волноводы: Пер. с англ. \ Под. Ред. В. В. Шевченко, – М.: Мир, 1980. – 656 с.

2. Семёнов А.С., Смирнов В.Л., Шмалько А.В. Интегральная оптика для систем передачи и обработки информации. – М.: Радио и связь, 1990. – 224 с.

3. Баскаков С. И. Электродинамика и распространение радиоволн.–М.: Высшая школа, 1992.- 416с

4. Никольский В. В., Никольский Т. И. Электродинамика и распространение радиоволн. – М.: Наука, 1989. –544 с.

5. Сборник задач по курсу “Электродинамика и распространение радиоволн” / Под. Ред. С.И. Баскакова. – М.: Высшая школа, 1981. – 208 с.

Дополнительный

6. Андрушко Л. М., Гроднев И. Н., Панфилов И.П. Волоконные оптические линии связи. – М.: Радио и связь, 1985. – 136 с.

7. Вайнштейн Л.А. Электромагнитные волны. – М.: Радио и связь, 1988. – 440 с.

8. Голубков С. В., Евтихиев Н.Н., Папуловский В.Ф. Интегральная оптика в информационной технике. – М.: Энергоатомиздат, 1985. – 151 с.

9. Жаблон К., Симон Ж-К. Применение ЭВМ для численного моделирования в физике. – М.: Наука, 1983. – 165 с.

ОГЛАВЛЕНИЕ

ПРЕДИСЛОВИЕ............................................................................................1

1. 1. ДИЭЛЕКТРИЧЕСКИЙ ВОЛНОВОД БАЗОВАЯ ЛИНИЯ ПЕРЕДАЧИ МИЛЛИМЕТРОВОГО И ОПТИЧЕСКОГО ДИАПАЗОНОВ ВОЛН............................................................................................................3

1.1. Особенности линии передачи на основе диэлектрических волноводов.....3

1.2. Лучевое представление распространения электромагнитных волн в диэлектрических волноводах......................................................................9

2. ВОЛНЫ В ПЛАНАРНОМ ДИЭЛЕКТРИЧЕСКОМ ВОЛНОВОДЕ...............14

2.1. Исходные соотношения строгой электродинамической теории..................14

2.2. Волны H-типа в асимметричном планарном диэлектрическом волново....18

2.3. Волны E–типа в асимметричном планарном диэлектрическом волноводе..23

2.4. Классификация мод в планарном диэлектрическом волновод......................24

2.5. Моды в симметричном планарном диэлектрическом волноводе..................30

2.6. Волны в планарном диэлектрическом волноводе на металлической подложке.........................................................................................................33

2.6.1. Волны E-типа в планарном диэлектрическом волноводе на металлической подложке.........................................................................................................34

2.6.2. Волны H-типа в планарном диэлектрическом волноводе на металлической подложке.........................................................................................................36

2.7. Мощность, переносимая модой по диэлектрическому планарному волноводу.......................................................................................................38

2.7.1. Переносимая мощность..................................................................................38

2.7.2. Соотношения ортогональности направляемых мод....................................39

2.8. Затухание в диэлектрическом волноводе......................................................40

2.9. H-образный металлодиэлектрический волновод...........................................43

3. ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ ДИСПЕРСИОННОГО УРАВНЕНИЯ................................................................................................44

3.1. Вводные замечания............................................................................................44

3.2. Метод “половинного деления”.........................................................................46

3.2.1. Алгоритм решения.........................................................................................47

3.2.2. Программная реализация алгоритма по методу "половинного деления" (дихотомии) на алгоритмическом языке Фортран-90..............................48

3.3. Метод аппроксимации......................................................................................52

3.3.1 Алгоритм решения..........................................................................................52

3.3.2. Программная реализация алгоритма по методу аппроксимации на алгоритмическом языке Фортран-90.........................................................56

4. УПРАЖНЕНИЯ И ЗАДАЧИ............................................................................60

БИБЛИОГРАФИЧЕСКИЙ СПИСОК....................................................................67

Дата добавления: 2015-08-31