Исследование усталостной деформации

4.1 Расчет максимальных нормальных (σ_max) и касательных (τ_max) напряжений [o1] на поверхности плоского образца при изгибе

Для вычисления напряжений и деформаций при испытании на усталость методом изгиба использовали представления механики сплошной среды [12]. Проведение расчета вызвано необходимостью оценки условий испытания на усталость при изгибе.

При испытании на усталость методом знакопеременного изгиба нижний конец образца закреплен в неподвижном захвате, а верхний захват совершает колебания с постоянной частотой и амплитудой. Можно рассматривать образец как балку с защемленным концом Балкой называется стержень, работающий на изгиб. На балку действуют силы и реакции.

Схема расчета следующая. Зная максимальную амплитуду изгиба – максимальный прогиб образца f_b, можно определить силу Р, которая действует на образец. Это значение используется для определения s_max в разных поперечных сечениях образца. По закону Гука определяем максимальную относительную деформацию, соответствующую напряжению. Считаем, что усталостные испытания проводили с постоянной суммарной амплитудой деформации e_а = const. Используя максимальные нормальные напряжения s_max, которые действуют в каждой точке на поверхности образца, оцениваем по критериям Мизеса и Треска максимальные касательные напряжения t_max, действующие на поверхности образца.

Рассматриваем образец как балку с защемленным концом (рисунок 16), на которую действует сосредоточенная сила Р.

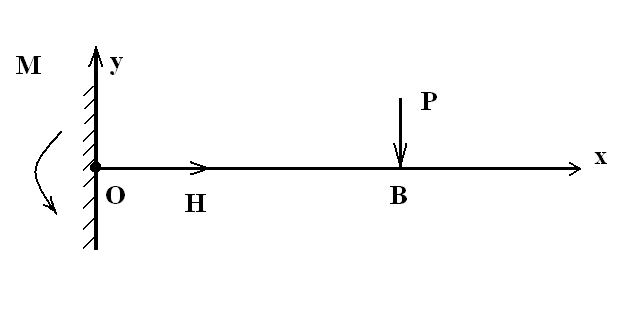
Рисунок 16 – Балка с защемленным концом [148]

Нормальные s и касательные t напряжения в поперечных сечениях балки являются функциями суммарного момента сил М и суммарной поперечной силы Q, действующих в этой плоскости. В предположении чистого изгиба, который фактически имеет место в нашем случае, относительное удлинение волокна, находящегося на расстоянии z от нейтрального слоя, равно:

e = = (3),

где r- радиус кривизны нейтрального слоя.

По закону Гука s = Е × e или

s = 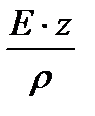(4)

Совместное решение уравнений (3) и (4) приводит к получению зависимостей:

или , (5)

где J_y = является осевым или экваториальным моментом инерции площади сечения относительно нейтральной оси y.

Подставляя (5) в (4) получаем:

s = (6)

нормальное напряжение в любой точке сечения, находящегося на расстоянии z от нейтральной оси. Максимальное нормальное напряжение для данного сечения достигается при z = z_max:

s_max = 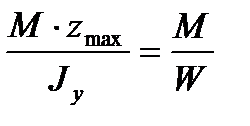, (7)

где величина W= является осевым моментом сопротивления сечения.

Вычисление моментов инерции сечения J_y для поперечного сечения балки шириной b и высотой h дает величину:

J_y= 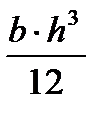, (8)

а момента сопротивления сечения W относительно нейтральной оси O_y при z_max = h/2 – величину:

W=J_y/z_max= 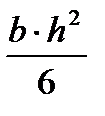(9)

Касательные напряжения в поперечных сечениях при изгибе вычисляются по формуле Журавского. Величина касательного напряжения t меняется по высоте прямоугольного сечения по закону параболы. При z = 0 t = t_max = , при z = ±h/2 t =0. При изгибе поперечная сила Q постоянна по длине образца и равна приложенной силе Р.

Деформацию балки в поперечном сечении при изгибе определяют через прогиб центра тяжести сечения y и угол поворота сечения Q. Оба параметра (y,Q) являются функциями расстояния х сечения от начала координат (точки защемления балки). Уравнение y = f(x) представляет уравнение изогнутой оси балки. Для получения зависимости y = f(x) используют установленную связь (5):

1/r(х) = , (10)

где r(х) – радиус кривизны участка изогнутой балки между смежными сечениями на расстоянии х от начала координат, М(х) – изгибающий момент в том же сечении, Е×J_y – жесткость балки. Используя зависимость кривизны балки от координат точек:

1/r(х) = , (11)

подставляют значение для кривизны в (4)

= (12)

и получают дифференциальное уравнение изогнутой оси или упругой линии. Для малых углов Q получают приближенное дифференциальное уравнение:

±E×J_y (13).

Интегрирование уравнения (12) дает значение: y= 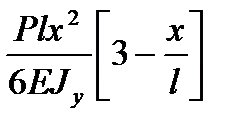и

максимальное значение прогиба f_b при х= l:

y = f_b = - 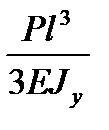(14)

Из выражения (14) находится значение силы Р, которое используем для определения максимальных значений нормального и касательно напряжений в поперечных сечениях образца. Определяем М = -Р×х₂, где величиной х₂ обозначили расстояние рассматриваемого сечения от верхнего захвата. По критерию Мизеса (t_y= 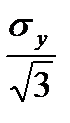) и по критерию Треска (t_y =s_y/2) определяем касательные напряжения на поверхности образца при s_y= s_max.

В работе исследовали и сравнивали разные материалы, поэтому для каждого из них были посчитаны свои напряжения (таблица 2.3, 2.4, 2.5). В таблице приведены расчетные значения максимальных нормальных напряжений s_max и касательные напряжения t_max в в поперечных сечениях образца. Определяем М=-Р·х, где величина х обозначили расстояние от верхнего захвата до рассматриваемого сечения. По критериям Мизеса () и Треска ()определенные касательные напряжения на поверхности. В таблицах 2.3-2.5 приведены расчетные значения максимальных нормальных напряжений s_max в поперечных сечениях образца и соответствующие касательные напряжения t_max на плоской поверхности образца, определенные по критериям Мезеса и Треска в зависимости от положения образца в нижнем захвате. Здесь же представлены максимальные относительные деформации e_max, соответствующее s_max. Расчет проводили для комнатной температуры. Размеры образца: длина l=37мм, высота h=1мм, ширина b=8мм, ширина головки b_г= 16мм (рисунок 10).

1. Алюминий особой чистоты. Модуль упругости Е=81000МПа [14], максимальный прогиб образца f_b=0,9мм (таблица 2).

Для особо чистого алюминия при комнатной температуре предел прочности составляет s_в=110,8МПа, предел текучести s_0,2=28,2МПа, а предел выносливости s_-1=26,5Мпа[13].

2. Технический алюминий. Модуль упругости Е=84900Мпа, максимальный прогиб образца f_b=1,5мм (таблица 3).

Длятехнического алюминия при комнатной температуре предел прочности составляет s_в=118,0МПа, предел текучести s_0,2=29,4МПа, а предел выносливости s_-1=78,5Мпа[13].

Таблица 2 – Расчет напряжений для алюминия особой чистоты

Сечение образца А-А	smax, МПа	e·10^4	tmax, MПа (по Мизесу)	tmax, MПа (по Треска)
А А	8,60		5,00	4,30
А А	6,58		3,80	3,29
А	6,81		3,93	3,40
А А	5,48		3,16	2,74

Таблица 3 – Расчет напряжений для технического алюминия

Сечение образца А-А	smax, МПа	e·10^4	tmax, MПа (по Мизесу)	tmax, MПа (по Треска)
А А	15,03		8,68	7,51
А А	11,50		6,64	5,74
А А	11,89		6,87	5,95
А А	9,57		5,53	4,79

Проведенный расчет показал, что в зависимости от положения образца в нижнем захвате в поперечных сечениях вблизи захвата значения s_max составляют: для о.ч. алюминия 5,48 ¸ 8,60МПа, для технического алюминия – 9,57 ¸ 15,03МПа, соответствующие им относительная деформация e_max равны: для о.ч. алюминия 7 ¸ 11, для технического алюминия – 11 ¸ 18; значения t_max рассчитанные по критерию Мезеса равны: для о.ч. алюминия 3,16 ¸ 5,00МПа, для технического алюминия – 4,79 ¸ 8,68МПа; а по критерию Треска: для о.ч. алюминия 2,74 ¸ 4,30МПа, для технического алюминия – 5,53 ¸ 7,51МПа. В работе использовали положение 3 в таблицах 2-3.

Таким образом, сравнивая с известными данными [13] (таблица 2), полученные значения напряжений достаточно корректны и могут использоваться для характеристики максимальной постоянной относительной деформации при знакопеременном изгибе.

Дата добавления: 2015-08-31