Коэффициенты переноса в газах

Для оценки коэффициентов переноса (диффузии, теплопроводности, вязкости) в газах используется следующий прием. Принимается, что вдоль каждой из осей координат движется по 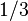всех молекул, 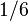- в положительном, 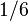- в отрицательном.

Рассмотрим перенос молекул вдоль оси 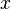. Число молекул, проходящих вверх за время свободного пробега через единицу площади равно

и вниз

здесь - средняя тепловая скорость, а 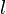- длина свободного пробега молекулы.

Коэффициент диффузии. Править

По определению диффузионного потока

Поскольку , то

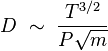
Коэффициент теплопроводности. Править

Будем считать что перемещение газа как целого вдоль оси 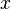нет. Это значит, что 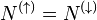. Пусть - энергия молекулы в точке 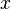, 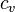- теплоемкость приходящееся на одну молекулу. Тогда согласно определению теплового потока

Отсюда следует

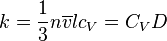
Вязкость. Править

С молекулярно кинетической точки зрения вязкость - это перенос тангенциальной компоненты импульса в направлении, перпендикулярном скорости течения. Пусть - средняя скорость упорядоченного движения молекул. Тогда импульс переносимый снизу в верхний слой газа, равен

а импульс переносимый вниз

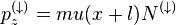
Здесь как и предыдущем

Получаем

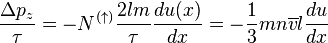
Отсюда находим

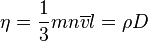
Бро́уновское движе́ние — беспорядочное движение микроскопических видимых, взвешенных в жидкости или газе частиц твердого вещества, вызываемое тепловым движением частиц жидкости или газа. Броуновское движение никогда не прекращается. Броуновское движение связано с тепловым движением, но не следует смешивать эти понятия. Броуновское движение является следствием и свидетельством существования теплового движения.

Броуновское движение — наиболее наглядное экспериментальное подтверждение представлений молекулярно-кинетической теории о хаотическом тепловом движении атомов и молекул. Если промежуток наблюдения достаточно велик, чтобы силы, действующие на частицу со стороны молекул среды, много раз меняли своё направление, то средний квадрат проекции её смещения на какую-либо ось (в отсутствие других внешних сил) пропорционален времени.

Броуновское движение происходит из-за того, что все жидкости и газы состоят из атомов или молекул — мельчайших частиц, которые находятся в постоянном хаотическом тепловом движении, и потому непрерывно толкают броуновскую частицу с разных сторон. Было установлено, что крупные частицы с размерами более 5мкм в броуновском движении практически не участвуют (они неподвижны или седиментируют), более мелкие частицы (менее 3 мкм) двигаются поступательно по весьма сложным траекториям или вращаются. Когда в среду погружено крупное тело, то толчки, происходящие в огромном количестве, усредняются и формируют постоянное давление. Если крупное тело окружено средой со всех сторон, то давление практически уравновешивается, остаётся только подъёмная сила Архимеда — такое тело плавно всплывает или тонет. Если же тело мелкое, как броуновская частица, то становятся заметны флуктуации давления, которые создают заметную случайно изменяющуюся силу, приводящую к колебаниям частицы. Броуновские частицы обычно не тонут и не всплывают, а находятся в среде во взвешенном состоянии.
Соотношение Эйнштейна

В физике (главным образом в молекулярно кинетической теории) соотношением Эйнштейна (также называемое соотношением Эйнштейна — Смолуховского) называется выражение, связывающее подвижность молекулы (молекулярный параметр) с коэффициентом диффузии и температурой (макро параметры). Оно было независимо открыто Альбертом Эйнштейном в 1905 году и Марианом Смолуховским (1906) в ходе работ по изучению броуновского движения:

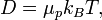
где 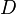— коэффициент диффузии, — подвижность частиц, — постоянная Больцмана, а 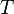— абсолютная температура.

Величина подвижности определяется из соотношения

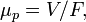
где — стационарная скорость перемещения частицы в вязкой среде под действием силы .

Это уравнение является частным следствием флуктуационно-диссипационной теоремы.

Дата добавления: 2015-08-31