
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Операции алгебры множеств
|
|
|
|
ЛАБОРАТОРНАЯ РАБОТА № 1
1.1 Цель работы
Закрепить знания основных положений и выполенеие операций алгебры множеств.
1.2 Темы лабораторной работы № 1
1. Реализовать операцию объединение множеств.
2. Реализовать операцию пересечение множеств.
3. Реализовать операцию разность множеств.
4. Реализовать операцию симметрическая разность множеств.
5. Реализовать операцию дополнение множества до универсума.
6. Реализовать булеан множеств.
7. Реализовать операцию декартово произведение множеств.
1.3 Основные орпределения
Основатель теории множеств немецкий математик Георг Кантор (Cantor) (1845-1918) дал такое определение множества:
множество - это любая совокупность определенных и различимых объектов нашей интуиции, мыслимое как единое целое.
Т.е. всякое множество однозначно и полностью определяется своими элементами.
Элементы множества – объекты, из которых оно состоит. Множества обозначаются большими латинскими буквами (A, B, C,…), элементы – малыми (a, b, c,…).
Через  обозначается отношение принадлежности элемента a множеству B: a
обозначается отношение принадлежности элемента a множеству B: a  B (“a принадлежит B”). Непринадлежность a множеству B обозначается а
B (“a принадлежит B”). Непринадлежность a множеству B обозначается а  В или а
В или а 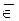 В.
В.
Если множество A состоит из элементов a,b,c,d, то это записывается таким образом: А={a,b,c,d}. Во множестве не может быть повторяющихся элементов.


 Если множество является элементом другого множества, то говорят о системе множеств и его обозначают большими прописными буквами Â={a,b,{d,c}}.
Если множество является элементом другого множества, то говорят о системе множеств и его обозначают большими прописными буквами Â={a,b,{d,c}}.
Множества могут быть конечными (т.е. состоящими из конечного числа элементов) и бесконечными.
Количество элементов, из которых состоит множество называется мощностью множества и обозначается 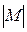 . Так в наших примерах имеем следующие мощности множеств:
. Так в наших примерах имеем следующие мощности множеств:  = 4,
= 4,  = 3.
= 3.
Мощность бесконечного множества называется континуум. Множество мощности 0 называется пустым и обозначается  или
или 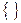 .
.
Если  =
=  , то множества А и В называются равномощными.
, то множества А и В называются равномощными.
Если всякий элемент множества А является элементом множества В, то А называется подмножеством В и обозначается А 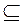 В. Знак
В. Знак 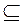 называется знаком нестрогого включения.
называется знаком нестрогого включения.
Множества A и B равны, если их элементы совпадают, иначе говоря, если А 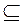 В и B
В и B 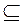 A.
A.
Если А 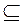 В и А
В и А  В, то А называется собственным или истинным подмножеством В и обозначается А
В, то А называется собственным или истинным подмножеством В и обозначается А  В. Знак
В. Знак  называется знаком строгого включения.
называется знаком строгого включения.
Справедливы две аксиомы теории множеств:
1. Аксиома объемности:
Множества А и В равны, если их элементы совпадают, т.е. А 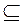 В и В
В и В 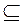 А.
А.
2. Аксиома существования:
Существует по крайней мере одно множество и это множество является пустым { }. Т.е. пустое множество является подмножеством любого множества.
1.4 Теоретические сведения
1.4.1 Операция объединение множеств
Объединением множеств А и В (обозначается А È В) называется множество, которое состоит из всех тех элементов, которые принадлежат хотя бы одному из множеств А или В. Символически это можно записать так:
А È В={ x ÷ x 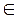 А V х
А V х  В}
В}
Например: А = {a, b, d}, B = {b, d, e, h}.
А È В = {a, b, d, e, h}.
Аналогично определяется объединение произвольной (в том числе бесконечной) совокупности множеств.
|
|
|
|
|
Дата добавления: 2015-08-31; Просмотров: 358; Нарушение авторских прав?; Мы поможем в написании вашей работы!